5.1. Операторное уравнение первого рода.
Возможность определения приближённых решений некорректно поставленных задач, устойчивых к малым изменениям исходных данных, основывается на дополнительной информации о решении, носящей качественный или количественный характер. Например, сужение класса возможных решений до компактного множества делает решение некорректной задачи устойчивым к малым изменениям исходных данных.
В качестве некорректно поставленной задачи рассматривается задача решения уравнения [8]
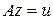
| (5.1) |
относительно функции z, где 
, 
; 
– метрические пространства. Оператор A отображает F на U. Предполагается, что существует обратный оператор A –1, не являющийся, вообще говоря, непрерывным.
Уравнение (5.1) с оператором A, обладающим указанными свойствами, называется операторным уравнением первого рода или просто уравнением первого рода.
5.2. Метод подбора.
Метод подбора решений широко используется в вычислительной практике. Он состоит в том, что для элементов z некоторого заранее заданного подмножества возможных решений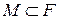 
вычисляется оператор Az, т. е. решается прямая задача. В качестве приближённого решения берётся такой элемент z 0 из множества M, на котором достигает минимума невязка [8]
 .
| (5.2) |
В случае точного решения z т невязка (5.2) равна нулю. Практически же её минимизация производится приближённо с использованием следующей леммы.
Лемма. Если отображение 
компакта F на множество U взаимно однозначно и непрерывно, то обратное отображение 
также непрерывно [8].
Таким образом, минимизирующая последовательность { zn } в методе подбора сходится к z т при n→∞, если 
и множество возможных решений M – компакт.
5.3. Корректность по А.Н. Тихонову.
Задача решения уравнения (5.1) называется корректной по Тихонову, если известно, что для точного значения u = u т существует единственное решение уравнения Az т = u т, принадлежащее заданному компакту M. В этом случае оператор A –1 непрерывен на множестве N = AM и, если вместо элемента u т известен элемент u δ такой, что 
и 
, то в качестве приближенного решения уравнения (5.1) с правой частью u = u δ можно взять элемент z δ = A –1uδ. При δ→0 z δ стремиться к z т. Множество 
, на котором задача решения уравнения (5.1) является корректно поставленной, называется классом корректности. Так, если оператор A непрерывен и осуществляет взаимно однозначное отображение, то компакт M, к которому принадлежит z т, является классом корректности для уравнения (5.1).
Таким образом, если задача корректна по Тихонову, то метод подбора успешно может быть применен к её решению.
5.4. Квазирешения.
Пусть оператор A в уравнении (5.1) вполне непрерывный. Построение устойчивого к малым изменениям правой части u приближённого решения уравнения (5.1) по формуле [8]
 ,
| (5.3) |
возможно в тех случаях, когда решение ищется на компакте 
и правая часть уравнения принадлежит множеству N = AM.
В практических задачах в силу погрешности исходных данных часто вместо точного значения правой части u т известно её приближённое значение u δ, которое может не принадлежать множеству N = AM. В этих случаях нельзя строить приближённое решение уравнения (5.1) по формуле (5.3), так как символ A –1 u δ может не иметь смысла. По этой причине вводится понятие квазирешения, а метод подбора при условии компактности множества M позволяет найти приближение к квазирешению.
Элемент 
, минимизирующий при данном u функционал 
на множестве M, называется квазирешением уравнения (5.1) на М [8]:
 .
| (5.4) |
Если M – компакт, то квазирешение существует для любого и если, кроме того, 
, то квазирешение z δ = z т. Квазирешение может быть и не одно – в этом случае под квазирешением понимается любой элемент из множества квазирешений.
Достаточные условия, при которых квазирешение единственно и непрерывно зависит от правой части u, определяются следующими теоремами.
Теорема. Если уравнение (5.1), Az = u может иметь на компакте M не более одного решения и проекция каждого элемента на множество N = AM единственна, то квазирешение этого уравнения единственно и непрерывно зависит от правой части u [8].
Теорема. Пусть уравнение (5.1), Az = u линейно, однородное уравнение Az = 0 имеет только нулевое решение, множество M выпукло, а всякая сфера в пространстве U строго выпукла. Тогда квазирешение этого уравнения единственно и непрерывно зависит от правой части u [8].
5.5. Приближённое нахождение квазирешений.
Будем полагать, что достаточные условия существования единственного квазирешения на заданном множестве M выполнены, т. е. множество M – выпуклый компакт и сфера в пространстве U строго выпукла. Пусть 
– возрастающая цепочка компактных замкнутых множеств Mn такая, что замыкание их объединения 
совпадает с M. Квазирешение уравнения (5.1) существует на каждом множестве Mn., но может быть не единственным. Обозначим через Tn совокупность всех квазирешений на множестве Mn [8].
Если в качестве Mn брать конечномерные (n -мерные) множества, то задача нахождения приближённого квазирешения на компакте M сводится к минимизации функционала ρ U (Az, u) на множестве Mn, т. е. к нахождению минимума функции n переменных [8].
5.6. Замена уравнения Az = u близким ему.
Идея замены уравнения (5.1), Az = u, в котором правая часть u не принадлежит множеству N = AM, близким ему уравнением, для которого задача нахождения решения устойчива к малым изменениям правой части и разрешима для любой правой части , принадлежит М.М. Лаврентьеву.
Пусть F ≡ U ≡ H – гильбертовы пространства, A – линейный, ограниченный, положительный и самосопряжённый оператор, Sn ≡ { x, || x || ≤ R, x ϵ F } есть шар радиуса R в пространстве F, B – вполне непрерывный оператор, определённый на Sn при любом R > 0. В качестве класса корректности M берётся множество Dn = BSn – образ шара Sn при отображении с помощью оператора В. Предполагается, что искомое точное решение z т уравнения (5.1) с правой частью u = u т существует и принадлежит множеству Dn. Уравнение (5.1) заменяется уравнением [8]
 ,
| (5.5) |
где E – единичный оператор; γ > 0 – числовой параметр. Решение уравнения (5.5) [8]
 ,
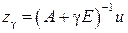| (5.6) |
при соответствующем выборе параметра γ принимается за приближённое решение уравнения (5.1).
5.7. Метод квазиобращения.
Задача Коши для уравнения теплопроводности с обратным течением времени является неустойчивой к малым изменениям начальных значений. Неустойчивость сохраняется и в случаях, когда решение подчиняется некоторым дополнительным граничным условиям. Для устойчивого решения таких задач разработан метод квазиобращения.
Рассмотрим прямую задачу. Пусть D – конечная область n -мерного евклидова пространства RN точек x = (x 1, x 2, …, xN), ограниченная кусочно-гладкой поверхностью S, а τ – время; φ(x) – заданная непрерывная в D функция. Прямая задача состоит в нахождении в области 
решения u = u (x, τ) уравнения [8]
 ,  ,
| (5.7) |
удовлетворяющего граничным условиям
 при 
| (5.8) |
и начальным условиям
 .
| (5.9) |
Решение краевой задачи (5.7)-(5.9) в виде u (x, τ; φ) существует и является единственным для каждой непрерывной в области определения функции 
.
Обратная задача состоит в нахождении функции φ(x) по известной функции u (x, τ; φ). В реальных задачах функция u (x, τ; φ) получается в результате измерений и, следовательно, известна приближённо. Будем полагать, что 
. Такая функция может и не соответствовать никакой функции 
, т. е. в классе функций C может не существовать решения обратной задачи. Поэтому рассматривается задача поиска обобщённого решения обратной задачи, определяемого следующим образом.
Пусть заданы число T > 0 и функция ψ(x), определённая в области D, 
. На функциях определён функционал [8]
 .
| (5.10) |
Обобщённым решением обратной задачи называется функция φ(x), на которой достигается [8]
 .
| (5.11) |
На некотором классе обобщённых функций φ(x) f 0 = 0. Поэтому рассматривается задача нахождения приближённого значения f 0 с заданным уровнем погрешности: для заданного числа ε > 0 найти функцию φε(x), на которой f (φε) ≤ ε.
Эта задача и решается методом квазиобращения, который состоит в замене оператора (∂/∂τ – Δ) «близким» ему оператором B γ, для которого задача с обращением отсчёта времени устойчива [8]:
 ,  ,  ,  ;
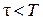| (5.12) |
 ;
| (5.13) |
 для  ,  .
| (5.14) |
Решив эту задачу, полагают [8]
 ,
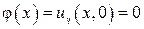| (5.15) |
Обычно в качестве оператора Bγ используется оператор [8]
 ,
| (5.16) |
и решается краевая задача (5.12)-(5.14), которая дополняется условием [8]
 для , .
| (5.17) |
Список литературы
1. Алифанов О.М., Артюхин Е.А., Ненарокомов А.В. Обратные задачи в исследовании сложного теплообмена. – М.: Янус-К, 2009. 300 с.
2. Панкратов Б.М. Методы отработки тепловых режимов технических систем и обратные задачи тепломассообмена // ИФЖ. 1989. Т. 56. № 3. С. 359-362.
3. Алифанов О.М., Вабищевич П.Н., Михайлов В.В. и др. Основы идентификации и проектирования тепловых процессов и систем: Учебное пособие. – М.: Логос, 2001. 400 с.
4. Голев Р.В., Четкарев В.А. Иерархическая идентификация тепловых процессов при разработке технических систем и технологий // ИФЖ. 1989. Т. 56. №3. С. 411-414.
5. Тихонов А.Н., Самарский А.А. Уравнения математической физики. Учебник для вузов. Изд. 5-е, стереотипное. – М.: Наука, 1977. 734 с.
6. Алифанов О.М. Обратные задачи теплообмена. – М.: Машиностроение, 1988. 280 с.
7. Тихонов А.Н., Васильева А.Б, Свешников А.Г. Дифференциальные уравнения. – М.: Наука. 1980. 288 с.
8. Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. Изд. 2-е. – М.: Наука. Физматлит, 1979. 288 с.
9. Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. –7-е изд.. М.: Физматлит, 2003. 572 с.