Лекция 8
Тема «Логические операции над высказываниями»
Цель: научиться формализовывать высказывания, строить таблицы истинности для формул логики, упрощать формулы логики с помощью равносильных преобразований.
План лекции:
1. Формулы логики высказываний.
2. Построение таблиц истинности логических формул.
3. Порядок действий в логических формулах.
4. Равносильность логических формул. Законы логики высказываний.
5. Тавтология, тождественно ложная формула, выполнимая формула.
Формулы логики высказываний
Определение. Под высказыванием понимают повествовательное предложение, которое может быть либо истинным, либо ложным.
Высказывания обозначаются большими латинскими буквами А, В, C,… или a, b,,…, х,…. Подобно тому, как из заданных чисел можно получить другие числа с помощью операций сложения, вычитания, умножения и деления, так из заданных высказываний получаются новые с помощью операций, имеющих специальные названия: конъюнкция, дизъюнкция, импликация, эквивалентность и отрицание. Эти операции означают соединение отдельных предложений связками «и», «или», «если…,то…», «тогда и только тогда, когда…» и присоединение к высказыванию частицы «не».
Определение. Формулой логики высказываний называется:
1) каждое отдельно взятое переменное высказывание;
2) если А, В - формулы логики высказываний, то формулами будут:
(А Λ В), (А V В), (А→В), (А↔В), (А);
3) других формул нет.
Для записи составного высказывания на формальном языке нужно выделить простые высказывания и логические связи между ними.
Пример 1. Записать с помощью формулы логики высказывание: «неверно, что если нет дождя, то будет солнечная погода, и дождь пойдет тогда и только тогда, когда будет ветер».
Решение.
Обозначим буквой А высказывание: «идет дождь», буквой В высказывание: «будет солнечная погода», буквой С высказывание: «будет ветер».
Разделим составное высказывание на простые и каждое запишем с помощью формулы логики:
«нет дождя» - А;
«если нет дождя, то будет солнечная погода» - А→В;
«дождь пойдет тогда и только тогда, когда будет ветер» - 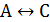 .
.
Между простыми высказываниями стоит союз «и», т.е. они соединяются с помощью конъюнкции и составное высказывание «если нет дождя, то будет солнечная погода, и дождь пойдет тогда и только тогда, когда будет ветер» запишется в виде:
( А→В) V (А↔С).
Т.к. перед этим составным высказыванием стоит слово «неверно», то нужно поставить отрицание над всей формулой.
В итоге заданное высказывание формализуется следующим образом:
(( А→В) V (А↔С))
Для каждого логического выражения можно построить таблицу истинности, позволяющую определить истинность или ложность логического выражения при всех возможных комбинациях исходных значений логических переменных.
Пример 2. Построить таблицу истинности для формулы А ˄ В.
Вначале подсчитаем сколько столбцов и строк будет в таблице. Если формула логики высказываний зависит от n переменных, то таблица истинности, построенная для этой формулы, содержит 2n строк. В представленной формуле два всказывания (А и В – 4 столбца) и две операции (А и А ˄ В – 2 столбца).
Получаем, что таблица истинности состоит из 5-ти строк и 4-ех столбцов.
Каждое из высказываний может быть либо истинным (1), либо ложным (0).
| А | В | А | А ˄ В |
С помощью определений логических операций заполняем таблицу, начиная с третьего столбца (А). Далее заполняем последний столбец: по определению конъюнкции высказываний (А ˄ В) будетистинно лишь в единственном случае, когда оба высказывания А и В истинны. В нашем случае это условие выполняется в третьей строке. В остальных случаях формула ложно (0).
Порядок выполнения действий в логических формулах:
1. отрицание ();
2. конъюнкция и дизъюнкция (˄, ˅);
3. импликация, эквиваленция (→, ↔).
Пример 3. Построить таблицу истинности для формулы X → (X ˄ Y).
1. в таблице 5 строк и 6 столбцов;
2. определяем порядок действий:
первое действие: X;
второе действие: Y;
третье действие: (X ˄ Y);
четвертое действие: X → (X ˄ Y).
3. строим и заполняем таблицу, пользуясь определениями логических операций.
| X | Y | X | Y | X ˄ Y | X → (X ˄ Y) |
Определение. Формулы А и В называют равносильными (обозначают А ≡ В), если они принимают одинаковые значения истинности на одних и тех же наборах значений
переменных высказываний.
Равносильные формулы имеют одинаковые таблицы истинности.
Пример 4. Установите равносильность формул:
а) (А) и А
Построим таблицу истинности.
| А | А | (А) |
Из построенной таблицы и определению равносильности высказываний получаем, что высказывания равносильны: (А) ≡ А.
б) А ˅ В и В ˅ А
| А | В | А ˅ В | В ˅ А |
Из построенной таблицы и определению равносильности высказываний получаем, что высказывания равносильны: А ˅ В ≡ В ˅ А.
в) А ˅ (В ˄ С) и (А ˄ В) ˅ (А ˄ С)
| А | В | С | В ˄ С | А ˅ (В ˄ С) | А ˄ В | А ˄ С | (А ˄ В) ˅ (А ˄ С) |
Из построенной таблицы и определению равносильности высказываний получаем, что высказывания равносильны: А ˅ (В ˄ С) ≡ (А ˄ В) ˅ (А ˄ С).
Наиболее часто используемые равносильные формулы получили название законов логики высказываний. Основные законы логики высказываний и их названия указаны в таблице.
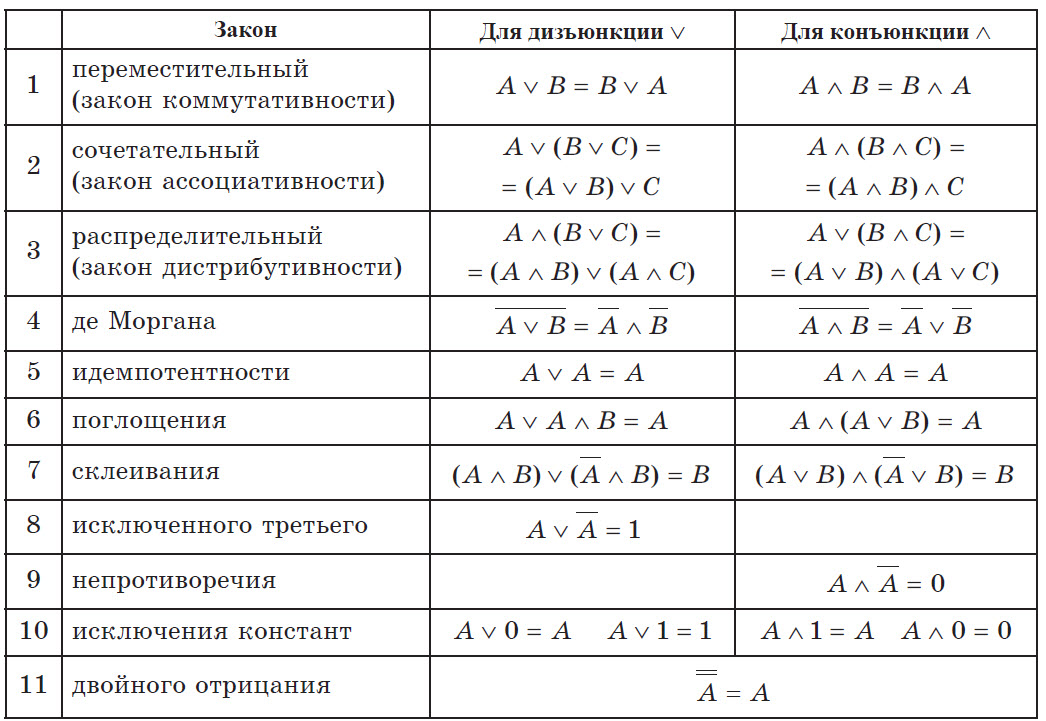
Примечание: обозначения Ā и А – отрицание высказывания А.
Определение. Формула называется тождественно истинной, или тавтологией, если она принимает значение истина при любом наборе значений переменных высказываний.
Определение. Формула называется тождественно ложной, если она принимает значение ложь, при любом наборе значений переменных высказываний.
Определение. Формула называется выполнимой, если существует хотя бы один набор значений переменных высказываний, на которых формула принимает значение
истинно.
Замечание: Любое тождественно истинное высказывание является выполнимым, обратное неверно.
Вывод: Установить является ли формула логики высказываний тождественно истинной, тождественно ложной или только выполнимой можно с помощью:
· построения таблиц истинности;
· равносильных преобразований.
Контрольные вопросы:
1. Что называется высказыванием?
2. Что называется формулой логики высказываний?
3. Запишите высказывание «Если светит солнце и не дует ветер, то не будет дождя» с помощью формулы логики.
4. Перечислите порядок действий в логических формулах.
5. Построить таблицу истинности для формул:
а) X ˅ (X ˅ Y) б) (А → В) ↔ (А → В)
6. Какие формулы называются равносильными?
7. Докажите равносильность формул (А ˄ В) ˄ С и А ˄ (В ˄ С).
8. Перечислите законы логики высказываний.
9. Какая формула называется тавтологией?
10. какая формула называется тождественно ложной?
11. Какая формула называется выполнимой?