Выпуклые многогранные множества
Раздел выпуклого анализа, посвященный выпуклым многогранным множествам, тесно связан с теорией систем линейных неравенств.Достаточно полное и детальное изложение теории систем линейных неравенств и выпуклых многогранных множеств можно найти в ([16], [23], [25]).
Определение 1. Множество 
называ- ется выпуклым многогранным, если оно представимо как пересечение конечного числа замкнутых полупространств.
Таким образом, например, множества решений системы линейных алгебраических уравнений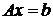 
либо неравенств 
, где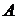 
– матрица размерности 
, 
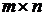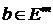, являются выпуклыми многогранными множествами.
Определение 2. Ограниченное выпуклое многогранное множество называется выпуклым мно-гогранником.
Легко увидеть, что справедливы следующие утверждения.
Теорема 1. Выпуклое многогранное множество является выпуклым множеством.
Теорема 2. Пусть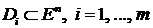 
– выпуклые многогранные множества. Тогда 
–
также выпуклое многогранное множество.
Особую роль в «устройстве» многогранного множества играет его граница. Следуя ([15], стр. 112 – 114), приведем следующие понятия.
Для каждого выпуклого многогранного мно-жества существует целое число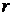 
(
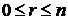) такое, что множество 
содержится в некотором линейном многообразии размерности 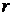( 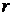-мерной плоскости), но не содержится целиком ни в какой (
)-мерной плоскости. При этом существует только одна такая 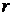-мерная плоскость, содержащая множество . Она называется несущей плоскостью многогранного множества , а число 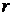называется размерностью этого множества. В частности, нульмерный многогранник представляет собой точку 
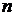-мерного про-странства. Несущей плоскостью одномерного мно-гогранного множества является прямая. В случае (
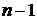)-мерного многогранного множества его несущей плоскостью является некоторая гиперплоскость. В случае же 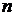-мерного многогранного множества несущая плоскость совпадает со всем пространством.
Граница любого 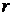-мерного многогранного
множества (при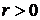 
) состоит из конечного числа ()-мерных многогранных множеств, причем все они имеют различные несущие плоскости. Эти многогранные множества называются ()-мерными гранями рассматриваемого 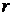-мерного многогранного множества. Каждая из этих ()-мерных
граней, в свою очередь, имеет (
)-мерные грани. Они также являются гранями исходного 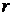-мерного многогранного множества. Аналогично определяются (
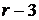)-мерные грани и грани меньших размерностей. Итак, у 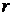-мерного многогранного множества могут быть грани размерностей , , …, 2, 1, 0. Одномерные грани называются ребрами. Ребро может быть отрезком, лучом, либо прямой. Нульмерные грани называются вершинами.
Приведем следующую теорему без доказательства.
Теорема 3. Для того, чтобы вектор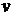 
из выпуклого многогранного множества был его вершиной, необходимо и достаточно, чтобы он был крайней точкой множества .
Определение 3. Множество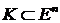 
называется выпуклым многогранным конусом, если оно одновременно является выпуклым многогранным
множеством и выпуклым конусом.
Легко увидеть, что справедлива следующая теорема.
Теорема 4. Пусть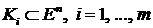 
– выпуклые многогранные конусы. Тогда 
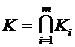– также выпуклый многогранный конус.
Нулевой вектор пространства принадлежит любому выпуклому многогранному конусу и является его единственной вершиной и как вершина
выпуклого конуса и, если он является крайней точкой, то и как вершина многогранного множества. Ребрами выпуклого многогранного конуса могут быть только лучи либо прямые.
Нетрудно увидеть, что луч является выпуклым многогранным конусом.
Приведем ряд утверждений о свойствах выпуклых многогранных множеств.
Теорема 5. Для того чтобы луч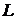 
из выпуклого многогранного конуса 
был его ребром, необходимо и достаточно, чтобы он был крайним лучом конуса .
Теорема 6. (О представлении выпуклого многогранного множества) Пусть выпуклое многогранное множество задано системой линейных неравенств , где 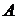– матрица размерности 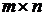, , 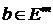ранг матрицы 
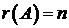. Тогда множество представимо в виде 
, где
выпуклый многогранник 
, 
– совокупность вершин множества , выпуклый многогранный конус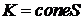 
, 
– множество направляющих векторов неограниченных ребер (лу-
чей) множества .
Теорема 7. Пусть выполнены условия теоремы 6. Тогда для 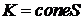в любой точке 
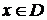справедливо включение 
.
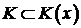Доказательство. Пусть точка 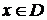,вектор 
. Покажем, что 
. По теореме 6 най
дутся векторы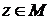 
и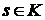 
такие, что 
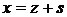. Пусть 
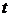– произвольное положительное число.Рассмотрим точку 
. Так как – выпуклый конус, вектор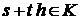 
. Поэтому согласно теореме 6 
,что и доказывает теорему.
Конусы опорных векторов
Ранее в параграфе 8 было введено множество 
векторов, опорных в точке 
ко множеству . Изучим свойства этих множеств.
Теорема 1. В любой точке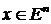 
множество 
является выпуклым замкнутым конусом.
Доказательство. Пусть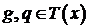 
, 
, 
. Для любого 
имеем 
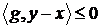и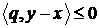 
, а значит, 
, то есть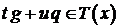 
. Итак, – выпуклый конус.
Проверим его замкнутость. Пусть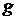 
– предельная точка конуса . Это означает, что существует последовательность 
такая, что 
. Для любой точки справедливы неравенства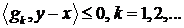 
Следовательно,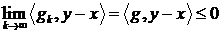 
, то есть 
. Что и означает замкнутость .
Легко увидеть, что справедливо следующее утверждение.
Теорема 2. Пусть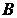 
и – множества из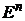 
,
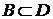. Тогда 
.
Следующая теорема непосредственно вытекает из теорем 2 и 1.
Теорема 3. Пусть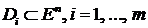 
, .
Тогда 
.
Задача построения конуса векторов опорных для данного множества в данной точке, вообще говоря, является достаточно сложной. Не существует явных формул или конечных алгоритмов, решающих эту задачу в общем случае. Однако для некоторых классов множеств эта задача решается сравнительно просто. Рассмотрим далее несколько случаев таких множеств, которые нам