Тема занятия: Виды связей и их реакции
1. Гладкая (без трения) опорная поверхность. Такая связь препятствует движению тела в одном направлении. Реакция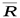 
гладкой поверхности направлены всегда по общей нормали к поверхности тела и поверхности связи в их точке касания (рис. 6).
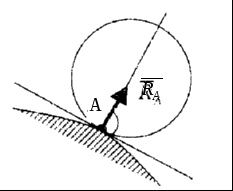Рис. 6
| 
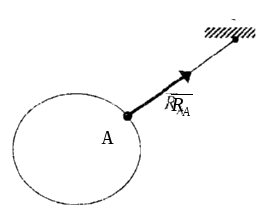Рис. 7
|
2. Гибкая связь. Реакции гибких связей всегда направлены вдоль самих связей к точке их подвеса (рис. 7).
3. Неподвижный цилиндрический шарнир (неподвижная шарнирная опора). Тело может только вращаться вокруг оси шарнира, перпендикулярной плоскости рисунка (рис. 8).
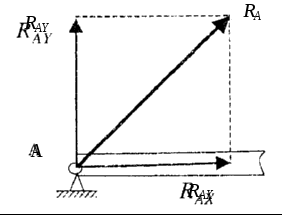
Рис. 8
Реакция RA проходит через ось шарнира и может иметь любое направление в плоскости. При решении задач целесообразно заменить ее составляющими RAX и RAY.
4. Подвижная шарнирная опора. Реакция такой опоры направлена по нормали к опорной поверхности (рис. 9).
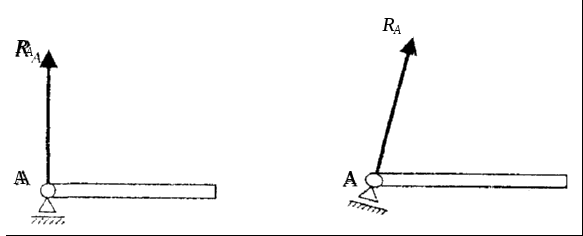
Рис. 9
5. Стержень. Стержень – прямолинейный невесомый элемент с двумя шарнирами на концах. При отсутствии нагрузки по его длине реакция стержня направлена вдоль его оси (рис. 10).
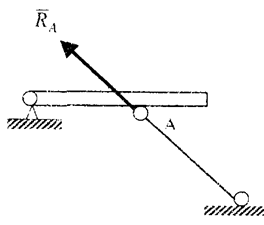Рис.10
| 
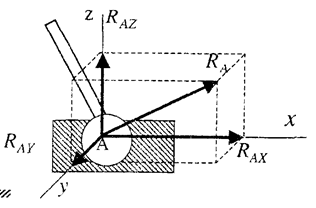Рис.11
|
6. Шаровой шарнир (рис. 11). Этот вид связи закрепляет какую-нибудь точку тела так, что она не может совершать линейных перемещений в пространстве, при решении задач целесообразно заменить эту силу ее составляющими RAX, RAY, RAZ.
7. Жесткая заделка (неподвижное защемление). Такая связь не допускает не только линейных перемещений, но и поворота тела (рис. 12).
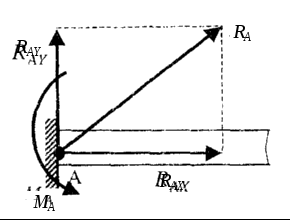
Рис. 12
Со стороны связи на тело действует реакция RA и момент MA (момент реакции заделки или реактивный момент). При решении задач рекомендуется силу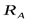 
заменить ее составляющими RAX и MA.
Равновесие несвободных тел изучается в статике на основании аксиомы связей:
-всякое несвободное тело можно рассматривать как свободное, если отбросить связи и заменить их действие соответствующими реакциями.
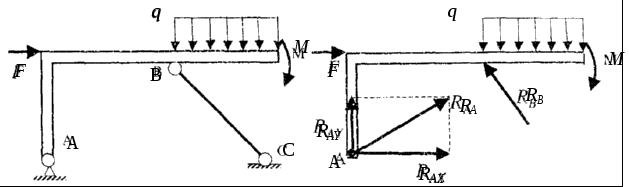
Например, элемент, для которого связями являются шарнирно-неподвижная опора А и стержень ВС (рис. 13,а), можно рассматривать как свободное тело, находящееся в равновесии под действием заданных сил и реакций связей RAX, RAY и RB (рис. 13,б). Значения этих реакций определяются из условий равновесия.
а) б)
Рис. 13
Плоская система сходящихся сил
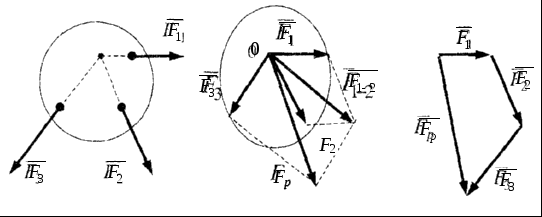
Система си, линии действия которых пересекаются в одной точке, называется системой сходящихся сил (рис. 14,а.)
а) б) в)
Рис. 14
Продолжив линии действия заданных сил до пересечения, перенесем точки приложения сил в точку пересечения (рис. 14,б).
Используя последовательно правило параллелограмма, получим:
; 
.
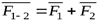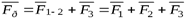В общем случае (для n сил):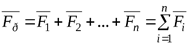 
.
Таким образом, система сходящихся сил приводится к равнодействующей, равной их векторной сумме и проходящей через точку их пересечения.
Равнодействующую можно определить графически с помощью векторного (силового многоугольника (рис. 14,в). Для этого последовательно в выбранном масштабе откладываются векторы заданных сил. Равнодействующей системы сил является вектор, соединяющий начало первого вектора с концом последнего.
Равнодействующую можно также определить аналитическим способом. Проекция силы на ось (рис. 15,а) определяется произведением модуля силы на косинус угла между направлением силы и направлением оси.
На рис. 15,б показан многоугольник сил. Из рисунка видно, что
,
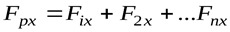где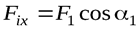 
; 
, …., 
.
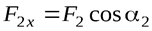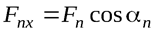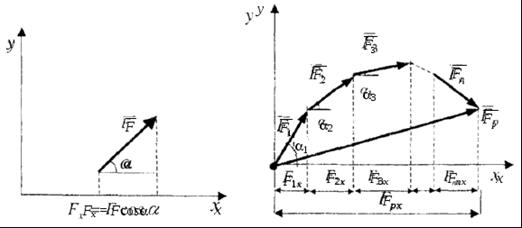
а) б)
Рис. 15
Аналогичные соотношения можно записать и для оси Y.
Т.е. проекция равнодействующей на какую-либо ось равна сумме проекций составляющих сил на ту же ось:
, 
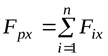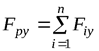(4)
Равнодействующая определяется так:
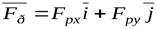(5)
где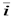 
, 
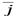– единичные векторы – орты.
Модуль равнодействующей равен
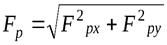(6)
Направление вектора равнодействующей определяется с помощью направляющих косинусов – косинусов углов между равнодействующей и осями x, y:
, 
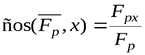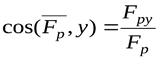(7)
Домашнее задание:
1. Просмотрите конспект
2. Посмотрите видео