Исследование автоколебаний в системе при включении на входе регулятора нелинейного звена

Рис. 3.7.1. Схема модели системы с включенным регулятором нелинейного звена; блоки Subsystem1,2 – те же, что и в схемах на рисунках 3.6.2 и 3.6.3.

Для возбуждения незатухающих автоколебаний данной системе требуется начальное воздействие. При отсутствии начальных условий для любых значений T_p и K_p автоколебания в системе не возникают. При подаче начального воздействия, даже небольшого по амплитуде (U = 0,05 B), в системе возникают незатухающие автоколебания.

Рис. 3.7.2. Возникновение незатухающих колебаний при небольшом начальном воздействии

Рис. 3.7.3. Незатухающие колебания при других начальных воздействиях

Из последнего рисунка видим, что автоколебания являются устойчивыми, т.е. при разных входных значениях колебания сходятся к одному и тому же уровню. Граничные значения коэффициента усиления и постоянной времени для инициирования незатухающих колебаний не зависят от подаваемых начальных условий: K_гр=0,03 (min, т.е. при меньших значениях коэффициента усиления колебания затухают), T_гр=1,4 (max, т.е. при больших значениях колебания затухают).

Частота колебаний не зависит от коэффициента усиления регулятора, так как заданная нелинейность однозначна. Получим зависимость амплитуды от коэффициента усиления регулятора.

Рис. 3.7.4. Зависимость амплитуды от коэффициента усиления регулятора

а) б)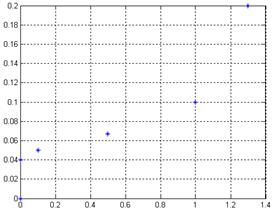

Рис. 3.7.5. Графики зависимости а) амплитуды, б) частоты колебаний от постоянной времени

4. Выводы:

Аналитическими методами было выяснено, что разомкнутая система устойчива, а замкнутая неустойчива. Границы области устойчивости были построены с помощью программы DCOM, осуществляющей D-разбиение. Построение линий равной степени устойчивости производилось в программе RTANALTI. Убедились, что области устойчивости о обоих случаях совпали, а значения линий равной степени устойчивости становились меньше при приближении к границе.

На полученных графиках были выбраны точки, для которых анализировались переходные процессы и рассчитывались их характеристики. Для оптимальных параметров переходный процесс имеет апериодический характер без перерегулирования.

С помощью аналитических методов были оценены характеристики и построены фазовый портрет нелинейной системы и примерный вид переходных процессов в ней.

Данная система была промоделирована в пакете Simulink, в результате чего были получены рассчитанные значения фазовых портретов и переходных процессов. Результаты оказались близкими к рассчитанным аналитическим способом. Было исследовано поведение системы при введении в ее состав обратной связи по скорости. На основании полученных результатов можно сделать вывод, что обратная связь по скорости в данном случае дает улучшение качества процесса – снижает колебательность, благодаря чему переходные процессы происходят без перерегулирования и с большим быстродействием.

Было исследовано возникновение автоколебаний в системе. На основании полученных данных был сделан вывод о том, что данной системе необходимо начальное возбуждение небольшой амплитуды, чтобы в ней возникли незатухающие колебания.