ВЕКТОРЫ
Основные определения
Опр. Вектором называется направленный прямолинейный отрезок.
Вектор характеризуется длиной и направлением.
Если даны начало вектора (точка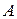 
) и его конец (точка 
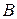), то вектор обозначается 
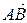, также можно обозначать векторы малыми латинскими буквами с чертой наверху 
.
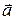Опр. Вектор, у которого начало в точке 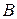, а конец в точке 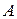, называется противоположным вектору 
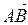. Вектор, противоположный вектору 
, обозначается 
.
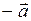Опр. Модулем вектора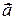 
называется его длина. Модуль вектора обозначается 
.
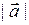Опр. Единичным называется вектор, длина которого равна единице, обозначается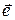 
.
Опр. Нуль – вектором называется вектор, у которого конец совпадает с началом, он обозначается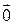 
.
Опр. Векторы и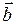 
называются коллинеарными, если они расположены на параллельных прямых или на одной прямой; записывается в этом случае 
.
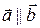Опр. Векторы и 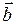называются сонаправленными, если они коллинеарны и направлены в одну сторону; обозначают: 
.
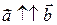Опр. Векторы и 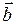называются противоположно направленными, если они коллинеарны и направлены в разные стороны; обозначают: 
.
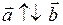Опр. Векторы и 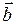называются равными, если они сонаправлены и имеют одинаковую длину; записывают: 
.
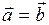Опр. Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях. Если среди трех векторов хотя бы один нулевой или два любые коллинеарны, то такие векторы компланарны.
Линейные операции над векторами
Линейными называются операции сложения, вычитания векторов и умножения вектора на число.
Опр. Суммой двух векторов и 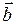называется вектор, полученный по правилу "треугольника": второй вектор 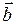откладывается так, чтобы его начало совпадало с концом первого вектора .
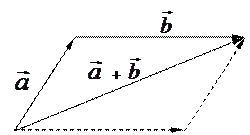
Рис. 3
Ту же самую сумму можно получить по правилу "параллелограмма"
второй вектор 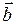откладывается из начала первого вектора , на этих векторах строится параллелограмм (рис.3) и суммой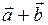 
в этом случае является диагональ этого параллелограмма.
Сложение нескольких векторов производится при помощи последовательного применения правила треугольника. (Рис.3-а, где изображено построение четырёх векторов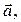 
).
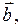
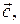
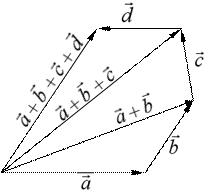
Свойства сложения векторов
1. Коммутативный закон сложения: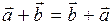 
.
2. Ассоциативный закон сложения: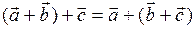 
.
3. 
.
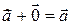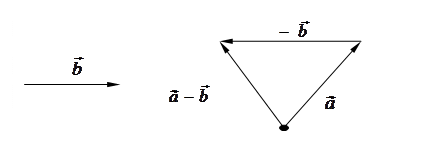
Опр. Разностью двух векторов 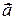и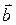 
называется сумма векторов 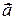и противоположного к вектору : 
.
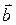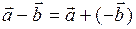Опр. Произведением вектора на действительное число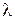 
называется вектор 
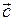, коллинеарный вектору , имеющий длину 
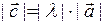и сонаправленный с вектором , если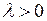 
; и противоположно направленный с вектором , если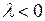 
.
Опр. Скалярным произведением векторов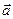 
и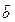 
называется число, равное произведению их модулей на косинус угла между ними:
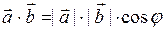(1)
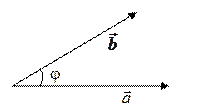
Рис. 1.
Свойства скалярного произведения:
1. 
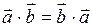(коммутативный закон).
2. 
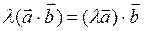(ассоциативный закон)
3. (
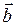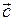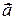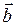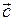+ ) = . + . (дистрибутивный закон).
4. Для того, чтобы два вектора были перпендикулярны, необходимо и достаточно, чтобы их скалярное произведение равнялось нулю.
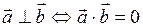
5. Скалярный квадрат вектора равен квадрату его модуля.
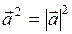
Таким образом, скалярное произведение векторов можно вычислить по формулам
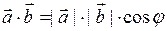и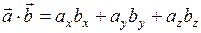 
,
если векторы заданны в координатной форме.
Угол между векторами
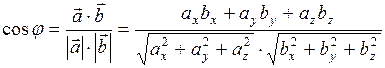
Условие перпендикулярности двух векторов и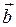 
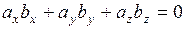
Условие коллинеарности двух векторов и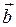
,
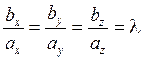т. е. одноименные координаты должны быть пропорциональны.
Пример 1. Установить острый или тупой угол между векторам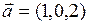и 
и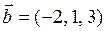 
.
Решение.
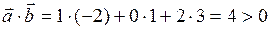
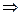угол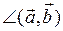 
- острый.
Ответ: острый.
Пример 2.
Найти косинус угла между векторам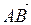и 
и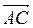 
.
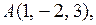
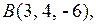
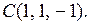
Решение.
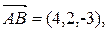
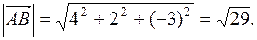
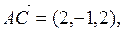
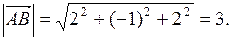
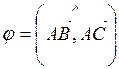
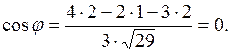
Опр. Векторным произведением вектора на вектор 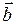называется вектор 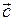, такой, что:
1) вектор 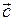перпендикулярен перемножаемым векторам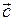 
, 
;
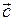
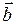2) модуль вектора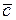 
определяется формулой:
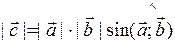
Векторное произведение будем обозначать 
.
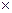
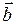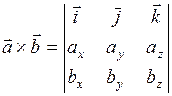(3)
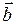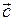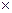
Опр. Смешанным произведением трёх векторов , и называется число, равно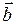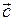е ( ) . , где
( 
) . = 
.
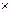
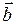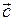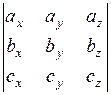Пример3. Вычислить определитель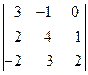 
.
Решение. Определитель третьего порядка можно вычислить по формуле
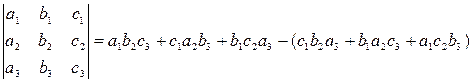
При этом полезна следующая схема. Первые три слагаемых – это произведения элементов, попавших на главную диагональ и в вершины двух треугольников (рис.1). Три слагаемых в скобках – это произведения элементов, попавших на побочную диагональ и в вершины двух других треугольников (рис.2).
 |  | ||
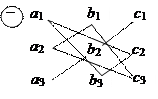Рис. 1 Рис. 2
Получаем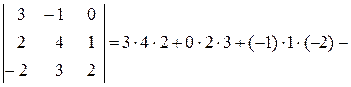 
.
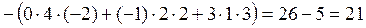