Таблица 3.1
Общий вид таблицы переходов автомата Мили
| am zf | a1 | ... | aM | ||
| z1 | f (a1,z1) | 
| f (aM,z1) | ||
|
|
|
| |||
| zF | f (a1,zF) | f (aM,zF) | |||
Таблица 3.2
Общий вид таблицы выходов автомата Мили
| am zf | a1 | ... | aM |
| z1 | l(a1,z1) |
| l (aM,z1) |
|
|
|
| |
| zF | l(a1,zF) | l (aM,zF) |
Таблицы переходов и выходов в совокупности содержат всю информацию об автомате, то есть определяют все компоненты множества (3.1), включая уравнения (3.5).
Например, из табл. 3.3 и 3.4 для автомата S1 имеем A={a1,a2,a3}, Z={z1,z2}, W={w1,w2,w3}.
Таблица 3.3
Таблица переходов автомата Мили S1
| am zf | a1 | a2 | a3 |
| z1 | a1 | a3 | a1 |
| zF | a3 | a1 | a2 |
Таблица 3.4
Таблица выходов автомата Мили S1
| am zf | a1 | a2 | a3 |
| z1 | w1 | w3 | w1 |
| zF | w3 | w1 | w2 |
Из табл. 3.3 имеем, например, d(а2, z1)=a3, d(a1, z1)=a2. Из табл. 3.4 имеем, например, l(a1, z1)w1, l(a3, z2)=w2.
Поскольку строки и столбцы таблиц переходов и выходов отмечены одинаковым образом, то всю информацию об автомате Мили можно задать одной совмещённой таблицей переходов и выходов. В этой таблице (Табл. 3.5 для автомата S1) на пересечении строки zf и столбца am находятся и состояние перехода as=d(am, zf) и выходной сигнал wg=(am, zf).
Таблица 3.5
Совмещённая таблица переходов
и выходов автомата Мили S1
| am zf | a1 | a2 | a3 |
| z1 | a2/w1 | a3/w3 | a1/w1 |
| z2 | a3/w3 | a1/w1 | a2/w2 |
2. Графическое задание автомата Мили. Граф автомата представляет собой ориентированный связный граф, вершины которого соответствуют состояниям автомата, а рёбра (дуги) – переходам между состояниями. В автомате Мили дуга, соответствующая переходу из am в as под воздействием сигнала z f, отмечается выходным сигналом wg=l(am,zf) и входным сигналом zf (Рис. 3.2).
Рис. 3.2. Фрагмент графа автомата Мили
Граф автомата Мили S1 (Рис. 3.3) имеем три вершины и шесть дуг, что соответствует произведению M·F.
Рис. 3.3. Граф автомата Мили S1
3. Табличное задание автомата Мура. Как следует из уравнений (3.6), выходной сигнал автомата Мура зависит только от его состояния. Поэтому автомат Мура задается одной отмеченной таблицей переходов (Табл. 3.6).
Таблица 3.6
Общий вид отмеченной таблицы переходов автомата Мура
| wg | l(a1) | l(aM) | |
| am z f | a1 | ... | aM |
| z1 | d(a1,z1) | ... | d(aM,z1) |
| ... | ... | ... | ... |
| zF | d(a1,zF) | ... | d(aM,zF) |
Например, из табл. 3.7 следуют все элементы множества S автомата Мура S2: A ={a1, a2, a3}, M =3, Z ={z1, z2}, F =2, W ={ w1, w2 }, G =2, d(a1, z1) =a2, λ(a1) = λ(a3) = w 2 и т.д.
Таблица 3.7
Отмеченная таблица переходов автомата Мура S2
| wg | w2 | w1 | w2 |
| am z f | a1 | a2 | a3 |
| z1 | a2 | a3 | a1 |
| z2 | a3 | a2 | a3 |
4. Графическое задание автомата Мура. Так как выходные сигналы автомата Мура зависят только от входных состояний, то каждой вершине графа автомата (Рис. 3.4) ставится в соответствие выходной сигнал.
Рис. 3.4. Фрагмент графа автомата Мура
Дуга графа автомата Мура отмечается только входным сигналом. Граф автомата Мура S2 приведен на рис. 3.5
Как видно из рис. 3.5, некоторые дуги образуют петли. Состояния, соответствующие петлям, называются ждущими. Автомат будет оставаться в ждущем состоянии до тех пор, пока не изменится значение входного
Рис. 3.5. Граф автомата Мура S2
сигнала. Так, для состояния a2 имеем d(a2, z2) =a2, то есть автомат S2 будет находиться в состоянии a2 пока входной сигнал не станет равным z1.
3.2. Синтез абстрактных автоматов
Условимся понимать под синтезом абстрактных автоматов задание закона функционирования автомата. Метод синтеза абстрактного автомата включает следующие этапы:
1. Формирование таблицы истинности комбинационной схемы, выполняющей аналогичную обработку параллельной информации.
2. Формирование входного и выходного алфавита.
3. Формирование графа автомата.
Рассмотрим некоторые примеры синтеза абстрактных автоматов.
Пример 2.1. Синтезировать абстрактный автомат Мили S3, на вход которого поступает трёхразрядный последовательный код x1x2x3, начиная с разряда x1. Если код содержит две последовательные единицы, то необходимо сформировать сигнал y1=1, в противном случае формируется сигнал y1=0.
Построим таблицу истинности для соответствующей параллельной комбинационной схемы (Табл. 3.8), то есть схемы, на вход которой сигналы x1x2x3 поступают одновременно.
Таблица 3.8
Таблица истинности параллельной КС
| x1 | x2 | x3 | y3 | x1 | x2 | x3 | у1 |
Чтобы получить входной алфавит, проанализируем столбцы x1-x3 таблицы. В каждом столбце находиться либо 0, либо 1. Таким образом, входной алфавит состоит из двух символов: z1 соответствует xl =0, z2 соответствует xl =1, где l =1, 2, 3.
Информация на вход схемы поступает последовательно, поэтому, например, переменная x1 не позволяет определить выходной сигнал. Если в течении двух тактов пришла комбинация 00, то необходимо установить y1=0, а если 11, то y1=1. Если приходит комбинация 01, то состояние выхода неизвестно. Таким образом, выходной алфавит автомата S3 содержит 3 буквы: w1, если y1=0, w2, если y1=1, и w3, если выходной сигнал еще не определен.
Итак, для автомата S3 Z ={z1, z2}, W ={ w1, w2, w3 }.
Рассмотрим процесс построения графа автомата S3. В момент времени t=0 автомат находится в состоянии a1 (Рис. 3.6, а).
В момент времени t = 0 на вход автомата могут прийти сигналы z1 или z2. Если Z(0) = z1, то x1 = 0 и это соответствует строкам 1-4 таблицы истинности. В строках 1-4 функция y1 может быть любой, следовательно переход (a1, z1) должен быть отмечен неопределённостью (Рис. 3.6, б). Аналогично, если Z(0)=z2, то x1 =1, что соответствует строкам 5-8 табл. 3.8. Этот переход также отмечается неопределённостью (Рис. 3.6, б). Итак, имеем a(1) = a2 = d(a1, z1) либо a(1) = a3 = d(a1, z2), λ(a1, z1) = λ(a1, z2) = = w (0) = w 3 (Рис. 3.6, б).
Если в момент времени t=1 автомат находится в состоянии a2, то сигнал z1 соответствует ситуации x1x2 = 00, так как a2 соответствует истории x1=0. В этом случае комбинация входных сигналов (строки 1 или 2 таблицы истинности) не может содержать двух последовательных единиц и необходимо сформировать сигнал w1.
Рис. 3.6. Процесс построения графа автомата S3
Распознавание входной комбинации завершено и автомат должен вернуться в состояние a1, чтобы иметь возможность обрабатывать следующую входную последовательность (Рис. 3.6, в). Если же на вход автомата приходит сигнал z2, то это соответствует ситуации x1x2 = 01 (строки 3 и 4), которая является неопределенной. Автомат переходит в состояние a4, соответствующее истории 01, и формирует сигнал w3 (Рис. 3.6, в).
Если в момент времени t=1 автомат находится в состоянии a3 (история x1 =1), то по входному сигналу z1 (x1x2 = 10) автомат переходит в состояние a1 и формирует выходной сигнал w1, что соответствует строкам 5 и 6 исходной таблицы истинности (Рис. 3.6, г). Если входной сигнал z(1)=z2, то это соответствует строкам 7 и 8 табл. 3.8. В этом случае автомат формирует сигнал w2 и переходит в состояние a1 (Рис. 3.6, г).
Если автомат находится в состоянии a4 (t =2), то приход z1 означает набор 010, а приход z2 – 011 (Рис. 3.6, д).
Теперь можно собрать граф автомата S3, совместив отдельные подграфы (Рис. 3.6), начиная с состояния a1 (Рис. 3.6, б). Граф автомата Мили S3 приведен на рис. 3.7.
Построим совмещенную таблицу переходов и выходов автомата S3 (Табл. 3.9), используя его граф. Процесс построения этой таблицы по графу очевиден.
Из рис. 3.7. и табл. 3.9 следует, что множество состояний автомата S3 содержит четыре элемента – A ={a1, a2, a3, a4}, M =4.
Рис. 3.7. Граф автомата Мили S3
Таблица 3.9
Совмещенная таблица переходов и выходов автомата Мили S3
| am zf | a1 | a2 | a3 | a4 |
| z1 | a2/w3 | a1/w1 | a1/w1 | a1/w1 |
| z2 | a3/w3 | a4/w3 | a1/w2 | a1/w2 |
Пример 3.2. Синтезировать абстрактный автомат Мура S4, выполняющий те же функции, что и автомат Мили S3.
Очевидно, что таблица истинности параллельной КС для автомата S4 совпадает с табл. 3.8, а алфавиты Z и W автомата S3: Z ={z1, z2}, W ={ w1, w2, w3 }.
Рассмотрим процесс построения графа автомата S4. В момент времени t=0 автомат находится в начальном состоянии a(0) = a1. Так как входная комбинация ещё не ясна, состояние a1 отмечается выходным сигналом w3. По сигналу z1 (x 1=0) автомат переходит в состояние a2, для которого выход не определен, по сигналу z2 – в состояние a3, в котором выход автомата также не определён (Рис. 3.8, а).
Если в момент времени t=1 автомат находится в состоянии a2, то приход z1 означает ситуацию 00, по которой автомат переходит в состояние a4, отмеченное выходным сигналом w 1 (y1=0). Если на вход автомата приходит сигнал z2, то это соответствует ситуации 01, для которой выход ещё не ясен. Автомат переходит в состояние a5, соответствующее w3 (Рис. 3.8, б).
Если a(1)=a3, то по сигналу z1 автомат формирует признак w 1 в состоянии a6, а по сигналу z2 – признак w 2 в состоянии a7 (Рис. 3.8, в).
Рис. 3.8. Процесс построения графа автомата S4
Если a(2)=a5, то сигнал z1 определяет набор 010, поэтому автомат переходит в состояние a8 с выходом w 1. Если входной сигнал равен z2, то это определяет набор 011, поэтому автомат переходит в состояние a9 и формирует сигнал w 2 (Рис. 3.8, г).
Подграфы для состояний a4, a6 – a9 совпадают, так как эти состояния соответствуют определенным ситуациям. Во всех случаях автомат переходит в состояние a1 независимо от входных сигналов (Рис. 3.8, д-е).
Объединение фрагментов даёт граф автомата S4 (Рис. 3.9).
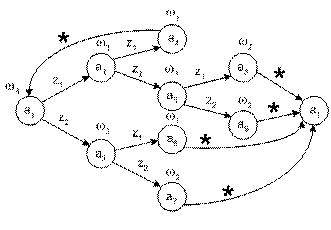
Рис. 3.9. Граф автомата Мура S4
Граф на рис. 3.9 содержит два состояния a1, что сделано для более наглядного изображения. Знак * над дугой означает, что переход не зависит от значений входных сигналов.
По этому графу строится отмеченная таблица переходов автомата Мура S4 (Табл. 3.10).
Таблица 3.10
Отмеченная таблица переходов автомата Мура S4
| wg | w3 | w3 | w3 | w1 | w3 | w1 | w2 | w1 | w2 |
| am z f | a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 | a9 |
| z1 | a2 | a4 | a6 | a1 | a8 | a1 | a1 | a1 | a1 |
| z2 | a3 | a5 | a7 | a1 | a9 | a1 | a1 | a1 | a1 |
Автоматы S3 и S4 выполняют одну и туже функцию, то есть они являются эквивалентными. Из анализа графов автоматов S3 и S4 можно сделать следующие выводы:
1. Автомат Мили содержит меньше состояний, чем эквивалентный автомат Мура.
2. Автомат Мили формирует выходные сигналы на один такт быстрее, чем эквивалентный автомат Мура.
Эти выводы справедливы и в общем случае.
Из анализа графа автомата S3 следует, что для состояний a3 и a4 по одинаковым входным сигналам формируются одинаковые выходные сигналы и происходит переход в состояние a1, то есть
λ(a3, z1) = λ(a4, z1) = w 1,
λ(a3, z2) = λ(a4, z2) = w 2,
d(a3, z1) = d(a4, z1) = a1,
d(a3, z2) = d(a4, z2) = a2.
Следовательно, состояния a3 и a4 полностью идентичны и одно из них можно исключить из графа автомата. Исключим, например, состояние a4, что приведет к минимизированному графу (Рис. 3.10).
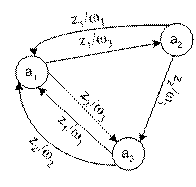
Рис. 3.10. Минимизированный граф автомата Мили S3
Поскольку теперь состояние a3 заменяет состояние a4, то все переходы с as = a4 заменяются на переходы с a5 = a3. Так, переход из a2 по z2 в минимизированном графе происходит в состояние a3.
Аналогично, в автомате Мура S4 состояния a4, a8, a6 идентичны, состояния a7, a9 также идентичны. Учет этого обстоятельства приводит к минимизированному графу автомата Мура S4 (Рис. 3.11), в котором группа состояний заменяется состоянием с наименьшим индексом, входящим в эту группу.
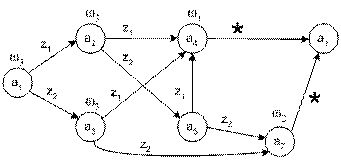
Рис. 3.11. Минимизированный граф автомата Мура S4
Анализ графа на рис. 3.11 показывает, что состояния a3 и a5 также идентичны и одно из них можно удалить, например a5. Таким образом, минимальный граф автомата S4 (Рис. 3.12) будет иметь только M=5 состояний.
Чем меньше состояний имеет граф автомата, тем проще схема соответствующего цифрового устройства. Для минимизации автоматов существуют формальные методы, которые всегда позволяют получать автоматы с минимальным числом состояний.
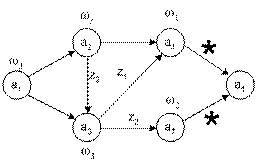
Рис. 3.12. Минимальный граф автомата Мура S4
3.3. Минимизация абстрактных автоматов
Классические методы минимизации абстрактных автоматов Мили были предложены Ауфенкампом Д. и Хоном Ф. и основаны на нахождении эквивалентных состояний. Состояния am,asÎA называются эквивалентными, если λ(am,B)=λ(as,B), где B – произвольная последовательность букв входного алфавита, называемая словом. Состояния am, as Î A называются i -эквивалентными, если λ(am,B i) = λ(as,B i), где B i – входные слова длины i (i =1, 2, …).
Основная идея алгоритма минимизации заключается в разбиении множества состояний A на классы эквивалентных состояний и замене всех состояний любого класса одним представителем этого класса. Этот алгоритм выполняется следующим образом:
1. Находят разбиения П1, П2, …, Пк множества А на классы 1-, 2-, …, к - эквивалентных состояний. Если на к +1-ом шаге получаем Пк = Пк+1, то разбиение П найдено (П = Пк). Число шагов на этом этапе не превышает М-1, где М – число состояний.
2. В каждом классе разбиения П выбирают по одному элементу, которые образуют множество А' состояний минимального автомата S'={A', Z, W, d', λ', a'1}, эквивалентного исходному автомату S={A, Z, W, d, λ, a1}.
3. Функции d' и λ' определяются на множестве А'´Z, для чего в таблицах переходов и выходов вычеркивают столбцы, соответствующие состояниям аm Î А', а внутри таблицы переходов состояния аm Î А' заменяют представителями класса эквивалентности, которому они принадлежат.
Рассмотрим пример применения этого алгоритма к автомату Мили S5, заданному совмещенной таблицей переходов (Табл. 3.11).
Таблица 3.11
Отмеченная таблица переходов автомата Мура S4
| am zf | a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 | a9 | a10 | a11 | a12 |
| z1 | a2/ w3 | a1/w1 | a1/w1 | a1/w1 | a1/w1 | a1/w1 | a1/w1 | a1/w1 | a1/w1 | a1/w1 | a1/w1 | a1/w1 |
| z2 | a3/w3 | a4/w3 | a1/w2 | a1/w2 | a1/w2 | a1/w2 | a1/w2 | a1/w2 | a1/w2 | a1/w2 | a1/w2 | a1/w2 |
Из табл. 3.11 следует, что А = {a1, …, a12}, Z = {z1, z2}, W = { w1, w2 }. Так как М=12, то минимизация автомата S5 потребует не более одиннадцати шагов.
Построим разбиение П1 = {B1, …,BI} множества А на классы 1-эквивалентных состояний, к которым относятся состояния am, as Î A, такие, что λ(am, z1) = λ(as, z1) и λ(am, z2) = λ(as, z2). Для автомата S5 П1 ={B1, B2}, где B1 ={a1, a2, a5, a7, a8}, B2 ={a3, a4, a6, a9, a10, a11, a12}. Для состояний класса B1 λ(am, z1) = w1, λ(am, z2) = w2, для состояний класса B2 λ(am, z1) = w2, λ(am, z2) = w1. Таким образом, разбиение П1 строится путем сравнения столбцов таблицы на совпадение выходных сигналов.
Построим таблицу разбиения П 2, заменяя состояния в табл. 3.11 соответствующими классами B i Î П1 (Табл. 3.12).
Очевидно, что 1-эквивалентные состояния будут 2-эквивалентными, если по входным сигналам они переводятся в одинаковые классы 1-эквивалентных состояний, то есть λ(am, zf) = λ(as, zf) = B i, где am, as Î B i. Из
табл. 3.12 находим разбиение П 2 = {C1, …, С4}, где С1={a1, a2}, С2={a5, a7, a8}, С3={a3, a4, a6, a9, a11}, С4={a10, a12}.
Таблица 3.12
Разбиение П 1 множества состояний автомата S5
| B i | B1 | B2 | ||||||||||
| am z f | a1 | a2 | a5 | a7 | a8 | a3 | a4 | a6 | a9 | a10 | a11 | a12 |
| z1 | B2 | B2 | B2 | B2 | B2 | B1 | B1 | B1 | B1 | B1 | B1 | B1 |
| z2 | B1 | B1 | B2 | B2 | B2 | B2 | B2 | B2 | B2 | B1 | B2 | B1 |
Так как П 1¹ П 2, то необходимо найти разбиение П 3, для чего строится таблица разбиения П 2 (Табл. 3.13). Очевидно, что 2-эквивалентные состояния будут и 3-эквивалентными, если по одинаковым входным сигналам они переходят в одинаковые классы 2-эквивалентных состояний. Это же правило можно применить по индукции для любого к.
Таблица 3.13
Разбиение П 2 множества состояний автомата S5
| C j | C1 | C2 | C3 | C4 | ||||||||
| am z f | a1 | a2 | a5 | a7 | a8 | a3 | a4 | a6 | a9 | a11 | a10 | a12 |
| z1 | C4 | C4 | C3 | C3 | C4 | C2 | C2 | C2 | C2 | C2 | C1 | C1 |
| z2 | C2 | C2 | C3 | C3 | C3 | C3 | C3 | C3 | C3 | C3 | C2 | C2 |
Из табл. 3.13 имеем П 3 = {D1, …, D5}, где D1={a1, a2}, D2={a5, a7}, D3={a8}, D4={a3, a4, a6, a9, a11}, D5={a10, a12}. Так как П 2 ¹ П 3, то найдем разбиение П 4 (Табл. 3.14).
Из табл. 3.14 имеем П 4 = {E1, …, E5}, где E1=D1={a1, a2}, E2=D2={a5, a7}, E3=D3={a8}, E4=D4={a3, a4, a6, a9, a11}, E5=D5={a10, a12}. Следовательно, П 3 = П 4 и процесс разбиения множества состояний завершен.
Таблица 3.14
Разбиение П 3 множества состояний автомата S5
| D l | D1 | D2 | D3 | D4 | D5 | |||||||
| am z f | a1 | a2 | a5 | a7 | a8 | a3 | a4 | a6 | a9 | a11 | a10 | a12 |
| z1 | D5 | D5 | D4 | D4 | D5 | D2 | D2 | D2 | D2 | D2 | D1 | D1 |
| z2 | D2 | D2 | D4 | D4 | D4 | D4 | D4 | D4 | D4 | D4 | D3 | D3 |
Выберем из каждого класса Е i Î П 4 по одному состоянию, например, выберем состояния с наименьшими индексами. Эти состояния образуют множество состояний минимального автомата Мили S5 A'={a1, a5, a8, a3, a10}. Удалим из исходной таблицы (Табл. 3.11) столбцы, отмеченные состояниями a2, a4, a6, a7, a9, a11, a12 Ï A'. В оставшихся столбцах заменим состояния asÏA' на представителей соответствующего класса эквивалентности. Например, λ(a3, z2)=a6 и a6ÏA', так как a6ÎE4, то λ(a3,z2)=a3. После аналогичных преобразований получим совмещенную таблицу переходов и выходов минимального автомата S5 (Табл. 3.15).
Таблица 3.15
Таблица переходов и выходов минимального автомата Мили S5
| am zf | a1 | a3 | a5 | a8 | a10 |
| z1 | a10/w3 | a5/w2 | a3/w1 | a10/w1 | a1/w2 |
| z2 | a5/w3 | a3/w1 | a3/w2 | a3/w2 | a8/w1 |
При минимизации автоматов Мура вводится понятие 0-эквивалентности и разбиения П 0. Состояния am,asÎА называются 0-эквивалентными, если λ(am)=λ(as). Дальнейший процесс минимизации аналогичен процессу минимизации автомата Мили. Рассмотрим применение этого метода к автомату Мура S6 (Табл. 3.16).
Таблица 3.16
Отмеченная таблица автомата Мура S6
| wg | w3 | w3 | w3 | w1 | w3 | w1 | w2 | w1 | w2 |
| am z f | a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 | a9 |
| z1 | a2 | a4 | a6 | a1 | a8 | a1 | a1 | a1 | a1 |
| z2 | a3 | a5 | a7 | a1 | a9 | a1 | a1 | a1 | a1 |
Из табл. 3.16 имеем разбиение П 0 = {B1, B2, B3}, где В1={a1, a2, a3, a5}, В2 = {a4, a6, a8}, В3 = {a7, a9}. Построим разбиение П 1, используя табл. 3.17. Из этой таблицы имеем разбиение П 1 = {C1, …, C5}, где С1={a1}, С2={a2}, С3={a1, a5}, С4={a4, a6, a8}, С5={a7, a9}.
Таблица 3.17
Разбиение П 0 автомата Мура S6
| B i | B1 | B2 | B3 | ||||||
| am z f | a1 | a2 | a3 | a5 | a4 | a6 | a8 | a7 | a9 |
| z1 | B1 | B2 | B2 | B2 | B1 | B1 | B1 | B1 | B1 |
| z2 | B1 | B1 | B3 | B3 | B1 | B1 | B1 | B1 | B1 |
Так как П 0 ¹ П 1, то найдем разбиение П 2, для чего строится табл. 3.18.
Таблица 3.18
Разбиение П 1 автомата Мура S6
| Ci | C1 | C2 | C3 | C4 | C5 | ||||
| am z f | a1 | a2 | a3 | a5 | a4 | a6 | a8 | a7 | a9 |
| z1 | C2 | C4 | C4 | C4 | C1 | C1 | C1 | C1 | C1 |
| z2 | C3 | C3 | C5 | C5 | C1 | C1 | C1 | C1 | C1 |
Из табл. 3.18 имеем П 2 = {D1, …, D5}, где D1=С1={a1}, D2=С2={a2}, D3=С3={a3, a8}, D4=С4={a4, a6, a8}, D5=С5={a7, a9}. Итак, П 2 = П 1 и классы эквивалентных состояний найдены. Построим A'={a1, a2, a3, a4, a7} и преобразуем табл. 3.16 в отмеченную таблицу минимального автомата Мура S6 (Табл. 3.19).
Таблица 3.19
Отмеченная таблица минимального автомата Мура S6
| wg | w3 | w3 | w3 | w1 | w2 |
| am z f | a1 | a2 | a3 | a4 | a7 |
| z1 | a2 | a4 | a4 | a1 | a1 |
| z2 | a3 | a3 | a7 | a1 | a1 |
Граф автомата Мура S6, построенный по табл. 3.19, совпадает с графом автомата Мура S4 (Рис. 3.12). Это вполне объяснимо, так как табл. 3.16 была построена по графу неминимального автомата Мура S4 (Рис. 3.11). Таким образом, формальный метод минимизации привел к таким же результатам, как и метод, основанный на эмпирических рассуждениях.
3.4. Структурный автомат
Структурный автомат – это устройство, реализующее закон поведения абстрактного автомата и представляющее собой сеть из логических элементов.
В отличии от абстрактного автомата, имеющего один входной сигнал и один выходной каналы, структурный автомат имеет:
1. L входных каналов, на которые поступают элементы множества X={ x1, …,xL }, где L=]log2F[, F=½Z½, Z={z1, …, zF} – входной алфавит абстрактного автомата.
2. N выходных каналов, с которых снимаются элементы множества Y={y1, …, yN}, где N=]log2G[, G=½W½, W={ w 1, …, w G} – выходной алфавит абстрактного автомата.
Для синтеза схемы структурного автомата необходимо наличие структурно полной системы элементарных автоматов, из которых и синтезируется схема. Существует общий конструктивный приём, называемый каноническим методом структурного синтеза, который позволяет синтезировать схему структурного автомата по таблицам или графу абстрактного автомата. Этот метод был предложен академиком В.М. Глушковым [6] и предполагает наличие структурно полной системы, включающей элементарные автоматы двух типов: автоматы с памятью, имеющие более одного состояния, и автоматы без памяти, имеющие одно состояние. Первые автоматы называются элементы памяти, вторые – логические элементы (И, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ).
Остановимся подробнее на элементах памяти, которые являются автоматами Мура с нетривиальной памятью, обладающими полнотой системы переходов и системы выходов. Рассмотрим автомат Мура S7 (Табл. 3.20).
Таблица 3.20
Отмеченная таблица переходов автомата Мура S7
| wg | w2 | w3 | w1 |
| am z f | a1 | a2 | a3 |
| z1 | a1 | a2 | a3 |
| z2 | a2 | a3 | a1 |
| z3 | a3 | a1 | a2 |
Автомат S7 обладает полнотой системы переходов, так как из любого состояния amÎA={a1, a2, a3} возможен переход в любое другое состояние. Автомат S7 обладает полнотой системы выходов, так как каждому состоянию amÎA соответствует уникальный выходной сигнал w g Î W={ w 1, w 2, w 3}. Это позволяет отождествить состояния и выходы. Автоматы с полнотой системы переходов и выходов называются полными автоматами. Использование полных автоматов в качестве элементов памяти структурных автоматов позволяет уменьшить число элементов памяти до
R=]logk M[,
где М – число состояний элемента памяти.
Канонический метод структурного синтеза основан на доказанной В.М. Глушковым теореме о структурной полноте, которая формулируется следующим образом:
Всякая система элементарных автоматов, которая содержит полный автомат Мура с нетривиальной памятью и какую-либо функционально полную систему логических элементов, является структурно полной. Существуют общий конструктивный прием (канонический метод структурного синтеза), позволяющий свести синтез структурного автомата к синтезу комбинационной схемы.
Результатом применения этого метода является система уравнений, задающая зависимость выходных сигналов и сигналов, подаваемых на входы запоминающих элементов, от сигналов, поступающих на входы автомата извне, и сигналов, снимаемых с выходов запоминающих элементов. Эти уравнения называются каноническими.
Схема структурного автомата (Рис. 3.13) состоит из комбинационной схемы КС и элементов памяти П 1, …, П R, которые образуют память автомата.
На входы КС поступают входные сигналы x1, …, x L и сигналы T1,…,TR, формируемые на выходах элементов памяти и образующие множество внутренних переменных T структурного автомата. На выходах КС формируются выходные сигналы y1,…,yN и функции возбуждения элементов памяти j1,…,jR, образующие множество функций возбуждения памяти автомата Ф. Комбинационная схема изображается в виде трапеции, а элементы памяти в виде прямоугольников, что отличает схемы без памяти и схемы с памятью.
Рис. 3.13. Схема структурного автомата
Комбинационная схема КС задается системой уравнений:
y1 = y1(x1,…,x L, T1,…TR);
.
.
.
yN = yN(x1,…,x L, T1,…TR);
j1 = j1(x1,…,x L, T1,…TR);
.
.
.
jR = jR(x1,…,x L, T1,…TR),
представляемой в сокращенной форме как
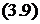Y = Y (X, T),
Ф = Ф (X, T).
Так как в системе (3.9) выходные сигналы зависят от в