Исходные данные
Таблица 1
| Вариант | Диаметр нити, мм | Материал Нити | 
| l, м | Параметры ГБС | Материал болтов | ||
| a, мм | b, мм | L, мм | ||||||
| Сталь | 1,5 | Сталь 3 |
Таблица свойств меди
Таблица 2
Плотность
 , кг/м3 , кг/м3
| Коэф. линейного
расширения

| Предел
прочности
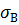 , МПа , МПа
| Модуль упругости Е, МПа |  °С °С
|
| 8,8×103 | 16,5×10-6 | 200-260 | 12,2×104 |
Таблица свойств стали
Таблица 3
| Материал | Предел
прочности
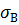 , МПа , МПа
| Предел
текучести
 , МПа , МПа
| Предел
выносливости
 , МПа , МПа
|
Расчет усилий в проводе и в точках подвеса
Определяем силы, действующие в точках (А, В) закрепления нити к кронштейнам (Приложение А).
Для материала нити сталь временный предел прочности  МПа (Таблица 3).
МПа (Таблица 3).
Плотность стали объемом  (таблица 3), а объемом
(таблица 3), а объемом  .
.
Сила тяжести (вес)  стали
стали  , а объемом
, а объемом  .
.
Площадь поперечного сечения заданного провода:
 Сила тяжести провода длиной 1 мм:
Сила тяжести провода длиной 1 мм:
 Сила тяжести провода длиной 1 м:
Сила тяжести провода длиной 1 м:
 Сила тяжести провода длиной 70 м Q=428,61 Н.
Сила тяжести провода длиной 70 м Q=428,61 Н.
Для материала проволоки сталь определяем допускаемые нормальные напряжения на растяжение:

Стрела провисания провода длиной 70 м с точками подвеса на одном уровне:

Сила натяжения провода в горизонтальной плоскости:

Длина провода с учетом провисания:

Полная реакция опоры:

Угол наибольшего провисания:

Вертикальная сила:

Расчет прочности группового болтового соединения кронштейна с консолью стойки
Схема силовой нагрузки на групповое болтовое соединение кронштейна (1) с консолью (2) со стороны гибкой нити (провода из меди) показана в
Приложении Б.
Полная сила натяжения нити 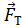 , действующая на кронштейн, приложена в точке А. Эту силу раскладываем на две составляющие силы: горизонтальную составляющую
, действующая на кронштейн, приложена в точке А. Эту силу раскладываем на две составляющие силы: горизонтальную составляющую  и вертикальную составляющую
и вертикальную составляющую  .
.
Вводим плоскую прямоугольную систему координат х и у. Определяем координаты центра тяжести площади стыка (точка С). В данном случае площадь стыка болтового соединения – прямоугольник 1234. Центр тяжести площади стыка находится в точке пересечения диагонали прямоугольника с координатами:  ;
;  . Находим расстояние (радиусы) от центра тяжести до центров отверстий под болты. Радиусы равны между собой.
. Находим расстояние (радиусы) от центра тяжести до центров отверстий под болты. Радиусы равны между собой.

Плечо силы  относительно центра тяжести С площади стыка соединения равно 360 мм (0,36 м).
относительно центра тяжести С площади стыка соединения равно 360 мм (0,36 м).
Плечо силы 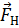 относительно центра тяжести С площади стыка соединения равно 110 мм (0,11 м).
относительно центра тяжести С площади стыка соединения равно 110 мм (0,11 м).
Момент силы  относительно центра тяжести равен:
относительно центра тяжести равен:

Момент силы 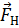 относительно центра тяжести равен:
относительно центра тяжести равен:

Суммарный момент равен:

Схему силовой нагрузки группового болтового соединения заменяем эквивалентной. По теореме Пуансо, силу  в плоскости ее действия на тело переносим параллельно самой себе в точку С. Эквивалентная система сил будет состоять из сдвигающей силы
в плоскости ее действия на тело переносим параллельно самой себе в точку С. Эквивалентная система сил будет состоять из сдвигающей силы  , приложенной в точке С, и момента пары сил, равного моменту силы.
, приложенной в точке С, и момента пары сил, равного моменту силы.
Сдвигающая сила равномерно распределяется между болтами. Сила реакции на сдвиг в каждом болте равна:

Силы реакций в болтах на действие вращающего момента прямо пропорциональны расстояниям от центра тяжести плоскости стыка (точка С) и направлены перпендикулярно к радиусам, соединяющим точку С и центры отверстий под болты. Так как, найденные ранее, радиусы равны между собой, то силы реакций во всех болтах также равны между собой:


Чертим вектора реакций болтов на сдвиг и на момент (Приложение Б). Вектора реакций на сдвиг направлены параллельно вектору силы  , но в противоположную сторону. Вектора реакций на вращающий момент направлены перпендикулярно к своим радиусам и в сторону противоположную моменту пары сил.
, но в противоположную сторону. Вектора реакций на вращающий момент направлены перпендикулярно к своим радиусам и в сторону противоположную моменту пары сил.
Находят суммарные силы реакций в болтах, как равнодействующие двух сил, приложенных к телу в одной точке. Наибольшая равнодействующая сила при заданных условиях будет суммарная реакция в третьем болте, так как угол между складываемыми векторами наименьший. Для определения этой равнодействующей необходимо найти угол между векторами сил реакций  (Приложение Б):
(Приложение Б):


Определяют суммарную силу реакции третьего болта:

При разных значениях радиусов определение суммарных сил реакций и нахождение при этом максимально нагруженного болта вычисления проводить необходимо для всех болтов.
Для определения геометрических параметров крепежной резьбы у наиболее нагруженного болта вначале рассчитываем максимальные усилия его завинчивания:

где k – рекомендуемый коэффициент запаса прочности;
 – коэффициент трения скольжения сухих поверхностей (сталь по стали). По условию задания кронштейн (1) и консоль (2) изготовлены из стали.
– коэффициент трения скольжения сухих поверхностей (сталь по стали). По условию задания кронштейн (1) и консоль (2) изготовлены из стали.
Находим допускаемые нормальные напряжения при растяжении для материала болтов из стали 10 при условиях, что болты устанавливают в отверстия с зазором и под контролем:

Определяем расчетный внутренний диаметр метрической резьбы по наиболее нагруженному болту.

По таблице стандарта выбираем по расчетному внутреннему диаметру ближайший больший внутренний диаметр стандартной резьбы с максимальным шагом и выписываем все ее параметры:
 34,093 мм d= 39мм
34,093 мм d= 39мм  36,402 мм p= 4 мм
36,402 мм p= 4 мм