Столбов Ю.В., Столбова С.Ю.
Омск
СибАДИ
2019
СОДЕРЖАНИЕ
Введение…………………………………………………………………………3
1. Теоретические основы статистических исследований точности
высотного положения оснований и покрытий автомобильных дорог………4
2. Исследование точности высотного положения конструктивных
слоев дорожных одежд…………………………………………………………12
3. Расчет допусков на геодезический контроль при устройстве
оснований и покрытий автомобильных дорог с автоматической системой задания отметок ………………………………………………………………...15
4. Детальная разбивка вертикальных (высотных) отметок поверхности конструктивных слоев дорожной одежды…………………………………….21
Библиографический список…………………………………………………….25
Приложение 1. Таблица значений функций Ф (х) – (ф-й Лапласса)………...26
Приложение 2. Таблица значений для интервальной оценки
математического ожидания «а»………………………………………………...27
Приложение 3. Таблица значений для оценки СКО «σ»……………………...28
Приложение 4. Критические точки распределения 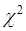 ………………………29
………………………29
Приложение 5. Значение предельных, среднеквадратических
погрешностей и расстояний удаления от реек от оптических нивелиров.......30
Приложение 6. Варианты заданий для статистического анализа точности высотного положения поверхностей конструктивных слоев оснований покрытий автомобильных дорог………………………………………………..31
ВВЕДЕНИЕ
Порядок выполнения расчетных работ с элементами научных исследований точности возведения конструкций зданий и сооружений.
1. После изучения теоретических основ приступаем к выполнению расчетов характеристик и параметров распределения отклонений амплитуд высотных отметок по вариантам.
2. Номера вариантов заданий выбираем из приложения 6 согласно двух последних цифр зачетной книжки с 01 до 30; с 31 до 60; 61 по 90 и т.д. (т.е. путем прибавления номера варианта с 01 до 30 «N+30»)
3. После статистической обработки амплитуд вертикальных (высотных) отметок вычисляем коэффициенты точности технологических процессов устройства конструктивных слоев дорожной одежды по выражению Тп= δн / m (где m – по результатам обработки данных, таблица 1).
4. По коэффициенту Тп рассчитываем допуски на контрольные измерения неровностей поверхностей конструктивных слоев дорожной одежды.
5. Для обеспечения необходимой точности геодезического контроля высотного положения конструктивных слоев рассчитываем максимальные расстояния реек от нивелиров Н-3 и Н-10, с доверительными вероятностями их обеспечения с Р= 0,9 и 0,95.
6. Вычисляем необходимую точность детальной разбивки высотных отметок поверхностей слоев дорожной одежды в зависимости от коэффициента точности Тп и определяем максимальные расстояния удаление реек от нивелиров Н-3 и Н-10.
ТЕОРЕТИЧЕСКИЕ ОСНОВЫСТАТИСТИЧЕСКИХ ИССЛЕДОВАНИЯ ТОЧНОСТИ ВЫСОТНОГО
ПОЛОЖЕНИЯ ОСНОВАНИЯ ПОКРЫТИЙ
АВТОМОБИЛЬНЫХ ДОРОГ.
При исследовании точности возведения автомобильной дороги было выполнено нивелирование поверхности конструктивных слоев дорожной одежды по левой, правой бровкам и центру ее полотна с шагом 5 м. По результатам нивелирования определялись отклонения вертикальных отметок от проектных, а по их значениям вычислялись амплитуды (алгебраическая разность) трех смежных точек с шагами 5, 10 или 20 м.
Оценку точности геометрических параметров конструкции слоев дорожной одежды можно выполнить с применением методов математической статистики и теории вероятностей, изложенных в работах [1], [2], [6], [7], [12], [15], [16], [17].
На основе статистического анализа результатов нивелирования поверхностей конструктивных слоев дорожной одежды устанавливалась закономерность распределения их действительных значений отклонений относительных вертикальных отметок от проектных. По значениям отклонений относительных вертикальных отметок вычислялись алгебраические разности (амплитуды) трех смежных точек вертикальных отметок поверхностей конструктивных слоев. Определялись статистические характеристики точности этих параметров. Статистический анализ точности осуществлялся в следующей последовательности:
– по результатам наблюдений получали выборки и определяли действительные отклонения параметров от их номинальных значений;
– рассчитывали статистические характеристики действительной точности параметра в выборках;
– проверяли статистическую однородность процесса, стабильность статистических характеристик в выборках и согласие опытного распределения действительных отклонений с теоретическим;
– оценивали точность технологического процесса.
Для изучения результаты разбивались в вариационные ряды. Совокупность измеренных и определенных величин разбивается на интервалы шириной h. Ширина интервала h вычислялась по формуле Стерджесса [12], [15], [16], [17]:
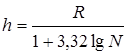 , (1.1.1)
, (1.1.1)
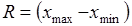 , (1.1.2)
, (1.1.2)
где  R – размах варьирования;
R – размах варьирования;
N – число измерений;
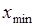 и
и 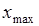 – соответственно минимальное и максимальное значение измеряемой величины.
– соответственно минимальное и максимальное значение измеряемой величины.
Формула (1.1.1) позволяет построить негромоздкий интервальный ряд, выявляющий характерные черты изучаемого явления. Количество интервалов k вычисляется по формуле:
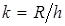 . (1.1.3)
. (1.1.3)
Наблюдаемые значения xi называют вариантами, числа наблюдений n -частотами, а их отношение к объему выборки называют относительными частотами или частостями, определяемыми по выражению:
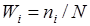 . (1.1.4)
. (1.1.4)
Статистическое распределение выборки - это перечень (вариант) интервалов и соответствующих им частот или частостей. Сумма частот, попавших в соответствующий интервал, принимается в качестве частоты этого интервала. Сумма всех частот равна объему выборки.
В качестве статистической оценки распределения результатов измерений x1,x2, x3,..., xn величины х принята выборочная средняя взвешенная:
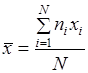 , (1.1.5)
, (1.1.5)
где N – число измерений; ni- частота; xi – результат измерения.
Рассеивание наблюдаемых значений количественного признака выборки относительно своего среднего значения  характеризуется выборочной дисперсией Д и выборочным среднеквадратическим отклонением
характеризуется выборочной дисперсией Д и выборочным среднеквадратическим отклонением 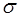 :
:
 , (1.1.6)
, (1.1.6)
 , (1.1.7)
, (1.1.7)
Генеральная дисперсия оценивается с помощью исправленной дисперсии и является несмещенной характеристикой:
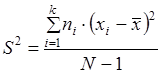 , (1.1.8)
, (1.1.8)
Для оценки среднеквадратического отклонения генеральной совокупности используется «исправленное» среднеквадратическое отклонение (среднеквадратическая погрешность), определяемое по формуле:
 , (1.1.9)
, (1.1.9)
Среднеквадратическая погрешность арифметического среднего М и среднеквадратическая погрешность самой среднеквадратической погрешности 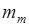 определяется по формулам:
определяется по формулам:
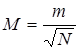 ; (1.1.10)
; (1.1.10)
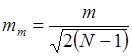 . (1.1.11)
. (1.1.11)
Оценки (1.1.5) – (1.1.9) будут точечными, которые определяются одним числом. При ограниченных объемах выборок следует использовать интервальные оценки, определяемые двумя числами и позволяющие установить точность и надежность оценок.
Для сравнения полученных из статистической обработки параметров распределения с нормативными величинами определяем доверительные интервалы среднего значения и дисперсии или среднеквадратического отклонения по выборочным характеристикам 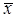 и m.
и m.
Доверительные интервалы задаются доверительной вероятностью  и уровнем значимости (точностью оценки)
и уровнем значимости (точностью оценки)  , учитывая, что исследуемые совокупности измерений имеют ограниченный объем и вероятность появления отклонений, превышающих по абсолютной величине
, учитывая, что исследуемые совокупности измерений имеют ограниченный объем и вероятность появления отклонений, превышающих по абсолютной величине 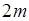 , очень мала.
, очень мала.
Для генеральной совокупности доверительные интервалы математического ожидания a и стандарта  определяются по выражениям [11], [17], [30], [36]:
определяются по выражениям [11], [17], [30], [36]:
 , (1.1.12)
, (1.1.12)
 , (1.1.13)
, (1.1.13)
где t – нормируемый множитель, зависящий от P; N – объем выборки.
Оценки математического ожидания а и стандарта 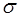 , приведенные выше, являются предельными и справедливыми при больших N.
, приведенные выше, являются предельными и справедливыми при больших N.
Для ограниченных объемов выборок, что имеет место у нас, для оценки a используется распределение Стьюдента и в выражение (1.1.12) вместо t вводится новый коэффициент 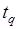 – нормируемый множитель, который зависит не только от P, но и от количества элементов в выборке. Тогда, для оценки а, при ограниченных объемах выборок, выражение будет иметь вид:
– нормируемый множитель, который зависит не только от P, но и от количества элементов в выборке. Тогда, для оценки а, при ограниченных объемах выборок, выражение будет иметь вид:
 , (1.1.14)
, (1.1.14)
При ограниченных объемах выборок, для оценок стандарта 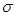 , используется распределение
, используется распределение 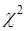 с
с 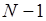 степенями свободы:
степенями свободы:
 , (1.1.15)
, (1.1.15)
где m – среднеквадратическая погрешность;
g – величина, зависящая от объема выборки и вероятности.
Для представления характера эмпирического распределения исследуемых величин строят гистограмму (кривую эмпирического распределения) и кривую теоретического распределений. Кривая эмпирического распределения строится по относительным частотам. Кривая теоретического распределения строится по значениям вероятностей 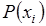 по интервалам, соответствующим эмпирическому распределению.
по интервалам, соответствующим эмпирическому распределению.
Многочисленные исследования точности процессов возведения сооружений показывают, что в случае налаженных технологических процессов распределение погрешностей их носит нормальный характер. В качестве нулевой статистической гипотезы при исследовании точности устройства конструктивных слоев дорожных одежд можно принять гипотезу о нормальном характере распределения ошибок, а вероятности 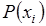 можно определить по формуле Лапласа:
можно определить по формуле Лапласа:
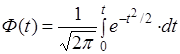 , (1.1.17)
, (1.1.17)
где 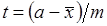 или
или  ;
;
a и b – границы интервала;
 – средняя взвешенная;
– средняя взвешенная;
m – исправленное среднеквадратическое отклонение (среднеквадратическая погрешность).
Гистограмма не дает полного представления о характере эмпирического распределения. Исследованиями процессов возведения сооружений в нашей стране и за рубежом установлено, что они в основном подчиняются закону нормального распределения. Поэтому в качестве статистической гипотезы принимаем, что распределения значений x подчиняются нормальному закону, т.е. это будет нулевая гипотеза. При проверке нулевой гипотезы могут возникнуть ошибки: первого рода, когда будет не принята правильная гипотеза и второго рода, когда принята неправильная гипотеза. Наиболее важным, для наших исследований, является устранение ошибки первого рода, а поэтому выбираем достаточно малый уровень значимости 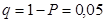 . В этом случае только в 5% из 100% можно допустить ошибку первого рода, а вероятность появления отклонений, превышающих по абсолютной величине 2 m, будет равна 0,05. Критерий, с помощью которого проверяют гипотезу о предполагаемом законе распределении, называется критерием согласия. Существует несколько критериев согласия, которые применяются в различных условиях: критерий
. В этом случае только в 5% из 100% можно допустить ошибку первого рода, а вероятность появления отклонений, превышающих по абсолютной величине 2 m, будет равна 0,05. Критерий, с помощью которого проверяют гипотезу о предполагаемом законе распределении, называется критерием согласия. Существует несколько критериев согласия, которые применяются в различных условиях: критерий 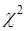 К. Пирсона, критерии А. Н. Колмогорова, Н. В. Смирнова, Б. С. Ястремского, В. И. Романовского и другие.
К. Пирсона, критерии А. Н. Колмогорова, Н. В. Смирнова, Б. С. Ястремского, В. И. Романовского и другие.
В случае принятия нулевой гипотезы о нормальном распределении, то в качестве критерия согласия удобно применить критерий (хи-квадрат), отличающейся большой чувствительностью к конкурирующей гипотезе.
При проверке нулевой гипотезы с применением критерия 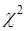 К. Пирсона используется случайная величина
К. Пирсона используется случайная величина
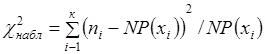 , (1.1.18)
, (1.1.18)
где n – эмпирические частоты;  - теоретические частоты; к - число интервалов;
- теоретические частоты; к - число интервалов;  - теоретическая вероятность попадания xi в интервал
- теоретическая вероятность попадания xi в интервал
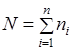 . (1.1.19)
. (1.1.19)
Если, вычисленный по результатам наблюдений, критерий К. Пирсона окажется меньше критического значения  , тогда нет оснований отвергать нулевую гипотезу. В случае
, тогда нет оснований отвергать нулевую гипотезу. В случае 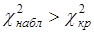 , то необходимо выполнить проверку гипотезы с помощью других критериев. Критические значения
, то необходимо выполнить проверку гипотезы с помощью других критериев. Критические значения 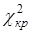 рассчитываются по принятому уровню значимости q и числу степеней свободы:
рассчитываются по принятому уровню значимости q и числу степеней свободы:
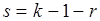 ,(1.1.20)
,(1.1.20)
где k – число интервалов;
r – число параметров предполагаемого распределения, которое оценивается по данным выборки.
Нормальное распределение оценивается двумя параметрами (а – математическим ожиданием, σ – среднеквадратическим отклонением), поэтому 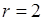 , тогда
, тогда 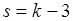 .
.
При малых выборках критерий 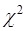 К. Пирсона может быть неэффективным, поэтому, когда величина вычисленного критерия равна или превышает критическое значение, то, чтобы не допустить ошибку первого рода и ошибочно не отвергнуть нулевую гипотезу о нормальном распределении, следует выполнить дополнительную проверку с применением других критериев. Например, критерий согласия Б. С. Ястремского менее чувствительный к конкурирующей гипотезе, и характеризуется [12], [92], [93] величиной:
К. Пирсона может быть неэффективным, поэтому, когда величина вычисленного критерия равна или превышает критическое значение, то, чтобы не допустить ошибку первого рода и ошибочно не отвергнуть нулевую гипотезу о нормальном распределении, следует выполнить дополнительную проверку с применением других критериев. Например, критерий согласия Б. С. Ястремского менее чувствительный к конкурирующей гипотезе, и характеризуется [12], [92], [93] величиной:
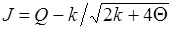 , (1.1.21)
, (1.1.21)
где k – количество интервалов в выборке,  при k< 20, величина Q вычисляется по формуле:
при k< 20, величина Q вычисляется по формуле:
 . (1.1.22)
. (1.1.22)
Нулевая гипотеза принимается при J< 3.
|
Таблица 1 - Статистическая обработка отклонений вертикальных (высотных) отметок от проектных.
Шаг нивелирования через 10 м

|
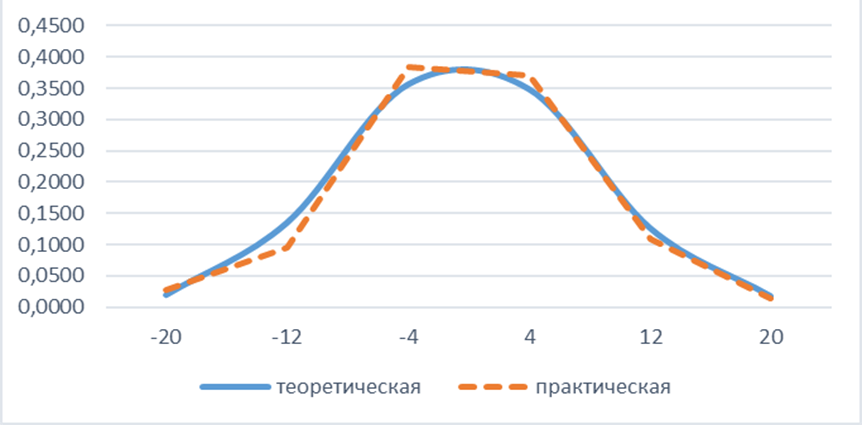
Рисунок 1 – Кривые эмпирического (практического) и теоретического (нормального) распределения амплитуд вертикальных отметок поверхности покрытия
Таблица 2 - Оценка сходимости эмпирических и теоретических частот
| интервалы | Частота, 
| Вероятность, 
| 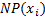
| 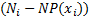
| 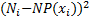
| 
| |
| а | б | ||||||
| -24 | -16 | 0,0186 | 1,3550 | 0,6450 | 0,4161 | 0,3071 | |
| -16 | -8 | 0,1340 | 9,7854 | -2,7854 | 7,7587 | 0,7929 | |
| -8 | 0,3550 | 25,9145 | 2,0855 | 4,3493 | 0,1678 | ||
| 0,3478 | 25,3912 | 1,6088 | 2,5881 | 0,1019 | |||
| 0,1261 | 9,2027 | -1,2027 | 1,4465 | 0,1572 | |||
| 0,0167 | 1,2224 | -0,2224 | 0,0495 | 0,0405 | |||
| 0,9982 | 1,5674 |
При К=6 число степеней свободы равно 3. c2 (0,05; 3) = 7,80. Так как 1,5674<7,80, то расхождение несущественно, гипотеза о нормально распределении не отвергается.
Произведем проверку критерия согласия Б.С.Ястремского.
Таблица 3 - Проверка критерия согласия Б.С. Ястремского
| Интервалы | Частота, 
| Вероятность, 
| 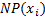
|  ) )
| 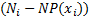
| 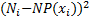
|  ) )
| 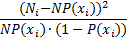
| |
| а | б | ||||||||
| -24 | -16 | 0,0186 | 1,3550 | 0,9814 | 0,6450 | 0,4161 | 1,3298 | 0,3129 | |
| -16 | -8 | 0,1340 | 9,7854 | 0,8660 | -2,7854 | 7,7587 | 8,4737 | 0,9156 | |
| -8 | 0,3550 | 25,9145 | 0,6450 | 2,0855 | 4,3493 | 16,7150 | 0,2602 | ||
| 0,3478 | 25,3912 | 0,6522 | 1,6088 | 2,5881 | 16,5595 | 0,1563 | |||
| 0,1261 | 9,2027 | 0,8739 | -1,2027 | 1,4465 | 8,0426 | 0,1799 | |||
| 0,0167 | 1,2224 | 0,9833 | -0,2224 | 0,0495 | 1,2020 | 0,0412 | |||
| 0,9982 | 1,8660 |
|
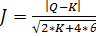
где K – количество интервалов в выборке;
Θ = 0,6 при К<20.
РАСЧЕТ ДОПУСКОВ НА ГЕОДЕЗИЧЕСКИЙ КОНТРОЛЬ

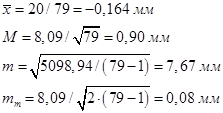
 Так как значение J<3, то расхождение несущественно, нулевая гипотеза о нормальном распределении не отвергается.
Так как значение J<3, то расхождение несущественно, нулевая гипотеза о нормальном распределении не отвергается.