Опять рассмотрим наши системы отсчёта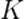 
и 
. Пусть точка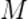 
движется вдоль общего направления осе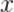й 
и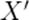 
(рис. 6).
| Рис. 6. К выводу закона сложения скоростей |
Пусть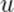 
— скорость точки 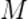в системе 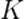; в системе скорость этой точки пусть будет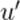 
. Как связаны друг с другом 
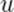и ?
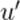Давайте вспомним, как выводится соответствующая формула в классической механике. Берём первое из равенств (11) с заменой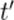 
на 
:
.
Переходим к бесконечно малым приращениям координат и времени:
.
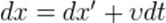Делим обе части на 
:
.
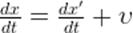Остаётся заметить, что 
, 
:
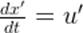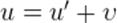. (12)
Вот мы и получили классический закон сложения скоростей, которым неоднократно пользовались при решении задач механики.
Однако данный закон не может быть верным в теории относительности. В самом деле, рассмотрим вместо точки 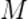световой сигнал в вакууме, мчащийся в системе со скоростью 
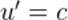. Согласно закону (12) получится, что скорость нашего сигнала в системе 
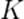будет равна 
. Но это противоречит принципу относительности, в силу которого скорость света в вакууме имеет одно и то же значение во всех инерциальных системах отсчёта.
Возникновение данного противоречия не удивительно: ведь вывод формулы (12) базируется на преобразованиях Галилея, которые в теории относительности уступают место преобразованиям Лоренца. Поэтому правильный закон сложения скоростей нужно выводить теперь из преобразований Лоренца.
Идея вывода — та же самая, что и для формулы (12). Мы исходим из того, что
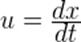,. (13)
В соотношениях (12) переходим к бесконечно малым приращениям координат и времени:
,.
Делим первое из данных равенств на второе:
.
Разделим числитель и знаменатель правой части на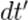 
:
.
Остаётся учесть соотношения (13) и написать:
. (14)
Это и есть релятивистский закон сложения скоростей, который приходит на смену классическому.
Теперь уже никакого противоречия не возникает: если скорость сигнала 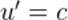в системе , то в системе 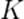его скорость равна:
,
как того и требует принцип относительности.
При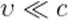 
формулы (14), как нетрудно видеть, переходят в формулы (12). Иными словами, при малых скоростях движения релятивистский закон сложения скоростей переходит в классический закон.
Релятивистская динамика
В классической динамике мы начали с законов Ньютона, потом перешли к импульсу, а после него — к энергии. Здесь мы ради простоты изложения поступим ровно наоборот: начнём с энергии, затем перейдём к импульсу и закончим релятивистским уравнением движения — модификацией второго закона Ньютона для теории относительности.
Релятивистская энергия
Предположим, что изолированное тело массы 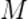покоится в данной системе отсчёта. Одно из самых впечатляющих достижений теории относительности — это знаменитая формула Эйнштейна:
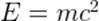(1)
Здесь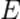 
— энергия тела, 
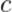— скорость света в вакууме. Поскольку тело покоится, энергия 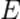, вычиляемая по формуле (1), называется энергией покоя.
Формула (1) утверждает, что каждое тело само по себе обладает энергией — просто потому, что оно существует в природе. Образно говоря, природа затратила определённые усилия на то, чтобы «собрать» данное тело из мельчайших частиц вещества, и мерой этих усилий служит энергия покоя тела. Энергия эта весьма велика; так, в одном килограмме вещества заключена энергия
Дж.
Интересно, какое количество топлива нужно сжечь, чтобы выделилось столько энергии? Возьмём, например, дерево. Его удельная теплота сгорания равна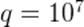 
Дж/кг, поэтому находим: 
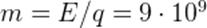кг. Это девять миллионов тонн!
Ещё для сравнения: такую энергию единая энергосистема России вырабатывает примерно за десять дней.
Почему столь грандиозная энергия, содержащаяся в теле, до сих пор оставалась нами незамеченной? Почему в нерелятивистских задачах, связанных с сохранением и превращением энергии, мы не учитывали энергию покоя? Скоро мы ответим на этот вопрос.
Поскольку энергия покоя тела прямо пропорциональна его массе, изменение энергии покоя на величину 
приводит к изменению массы тела на
.
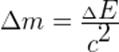Так, при нагревании тела возрастает его внутренняя энергия, и, стало быть, масса тела увеличивается! В повседневной жизни мы не замечаем этого эффекта ввиду его чрезвычайной малости. Например, для нагревания воды массой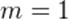 
кг на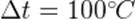 
(удельная теплоёмкость воды равна 
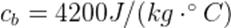) ей нужно передать количество теплоты:
Дж.
Увеличение массы воды будет равно:
кг.
Столь ничтожное изменение массы невозможно заметить на фоне погрешностей измерительных приборов.
Формула (1) даёт энергию покоящегося тела. Что изменится, если тело движется?
Снова рассмотрим неподвижную систему отсчёта 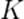и систему , движущуюся относительно 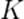со скоростью 
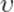. Пусть тело массы 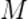покоится в системе ; тогда энергия тела в системе есть энергия покоя, вычисляемая по формуле (1). Оказывается, при переходе в систему 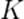энергия преобразуется так же, как и время — а именно, энергия тела в системе 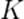, в которой тело движется со скоростью 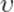, равна:
(2)
Формула (2) была также установлена Эйнштейном. Величина 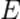— это полная энергия движущегося тела. Поскольку в данной формуле 
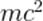делится на «релятивистский корень», меньший единицы, полная энергия движущегося тела превышает энергию покоя. Полная энергия будет равна энергии покоя только при 
.
Выражение для полной энергии (2) позволяет сделать важные выводы о возможных скоростях движения объектов в природе.
1. Каждое массивное тело обладает определённой энергией, поэтому необходимо выполнение неравенства
.
Оно означает, что 
: скорость массивного тела всегда меньше скорости света.
2. В природе существуют безмассовые частицы (например, фотоны), несущие энергию. При подстановке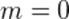 
в формулу (2) её числитель обращается в нуль. Но энергия-то фотона ненулевая!
Единственный способ избежать здесь противоречия — это принять, что безмассовая частица обязана двигаться со скоростью света. Тогда и знаменатель нашей формулы обратится в нуль, так что формула (2) попросту откажет. Нахождение формул для энергии безмассовых частиц не входит в компетенцию теории относительности. Так, выражение для энергии фотона устанавливается в квантовой физике.
Интуитивно чувствуется, что полная энергия (2) состоит из энергии покоя и собственно «энергии движения», т. е. кинетической энергии тела. При малых скоростях движения это показывается явным образом. Используем приближённые формулы, справедливые при 
:
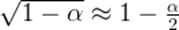(3) 
(4)
С помощью этих формул последовательно получаем из (2):
(5)
Таким образом, при малых скоростях движения полная энергия сводится просто к сумме энергия покоя и кинетической энергии. Это служит мотивировкой для определения понятия кинетической энергии в теории относительности:
. (6)
При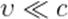 
формула (6) переходит в нерелятивистское выражение 
.
Теперь мы можем ответить на заданный выше вопрос о том, почему до сих пор не учитывалась энергия покоя в нерелятивистских энергетических соотношениях. Как видно из (5), при малых скоростях движения энергия покоя входит в полную энергию в качестве слагаемого. В задачах, например, механики и термодинамики изменения энергии тел составляют максимум несколько миллионов джоулей; эти изменения столь незначительны по сравнению с энергиями покоя рассматриваемых тел, что приводят к микроскопическим изменениям их масс. Поэтому с высокой точностью можно считать, что суммарная масса тел не меняется в ходе механических или тепловых процессов. В результате суммы энергий покоя тел в начале и в конце процесса попросту сокращаются в обеих частях закона сохранения энергии!
Но такое бывает не всегда. В других физических ситуациях изменения энергии тел могут приводить к более заметным изменениям суммарной массы. Мы увидим, например, что в ядерных реакциях отличия масс исходных и конечных продуктов обычно составляют доли процента.Скажем, при распаде ядра урана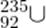 
суммарная масса продуктов распада примерно на 
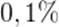меньше массы исходного ядра. Эта одна тысячная доля массы ядра высвобождается в виде энергии, которая при взрыве атомной бомбы способна уничтожить город.
При неупругом столкновении часть кинетической энергии тел переходит в их внутренюю энергию. Релятивистский закон сохранения полной энергии учитывает этот факт: суммарная масса тел после столкновения увеличивается!
Рассмотрим в качестве примера два тела массы 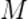, летящих навстречу друг другу с одинаковой скоростью 
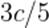. В результате неупругого столкновения образуется тело массы 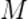, скорость которого равна нулю по закону сохранения импульса (об этом законе речь впереди). Согласно закону сохранения энергии получаем:
,
,
,
.
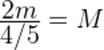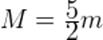Мы видим, что, — масса образовавшегося тела превышает сумму масс тел до столкновения. Избыток массы, равный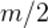 
, возник за счёт перехода кинетической энергии сталкивающихся тел во внутреннюю энергию.
Релятивистский импульс.
Классическое выражение для импульса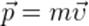 
не годится в теории относительности — оно, в частности, не согласуется с релятивистским законом сложения скоростей. Давайте убедимся в этом на следующем простом примере.
Пусть система движется относительно системы 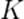со скоростью 
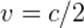(рис. 1). Два тела массы 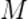в системе летят навстречу друг другу с одинаковой скоростью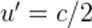 
. Происходит неупругое столкновение.
| Рис. 1. К закону сохранения импульса |
В системе тела после столкновения останавливаются. Давайте, как и выше, найдём массу 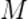образовавшегося тела:
,
откуда
.
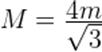Теперь посмотрим на процесс столкновения с точки зрения системы 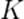. До столкновения левое тело имеет скорость:
.
Правое тело имеет скорость:
.
Нерелятивистский импульс нашей системы до столкновения равен:
.
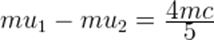После столкновения получившееся тело массы 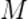двигается со скоростью 
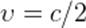. Его нерелятивистский импульс равен:
.
Как видим,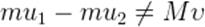 
, то есть нерелятивистский импульс не сохраняется.
Оказывается, правильное выражение для импульса в теории относительности получается делением классического выражения на «релятивистский корень»: импульс тела массы 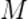, двигающегося со скоростью 
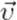, равен:
. 7
Давайте вернёмся к только что рассмотренному примеру и убедимся, что теперь с законом сохранения импульса всё будет в порядке.
Импульс системы до столкновения:
.
Импульс после столкновения:
Вот теперь всё правильно: 
!