Снова рассмотрим вагон, который движется со скоростью 
. Предположим, что пассажир вагона подбрасывает яблоко; оно летит вертикально вверх, возвращается, и пассажир ловит его.
В системе отсчёта вагона события «яблоко брошено» и «яблоко поймано» происходят в одной точке. Промежуток времени между этими событиями, т. е. время полёта яблока в системе отсчёта вагона, измеряется по одним и тем же часам, расположенным в точке броска-ловли.
Но в системе отсчёта земли наши события происходят в различных пространственных точках. Момент броска яблока фиксируется по часам, расположенным в исходной точке, а момент ловли — по другим часам, расположенным в той точке, куда переместится вагон за время полёта яблока. Эти двое часов синхронизированы по правилу Эйнштейна. Время полёта яблока в системе отсчёта земли — это разность показаний вторых часов в момент ловли и первых часов в момент броска.
И вот оказывается, что время полёта яблока, измеренное по вагонным часам, будет меньше времени полёта, измеренного по часам на земле!
Разобраться в этом не сложно. Давайте только заменим яблоко на световой сигнал, который бегает между горизонтальными зеркалами, расположенными внутри вагона (рис. 3). Тем самым мы максимально упростим себе задачу.
| Рис. 3. Промежуток времени относителен |
Сначала рассмотрим ход сигнала в системе отсчёта вагона. Сигнал выходит из точки 
, идёт вертикально вверх, отражается от зеркала и возвращается назад в точку (рис. 3, слева).
Время распространения сигнала от нижнего зеркала к верхнему и обратно, измеренное по часам , обозначим 
. Если 
— расстояние между зеркалами, то выполнено соотношение
. 1
Теперь перейдём в систему отсчёта земли. Здесь сигнал будет двигаться между зеркалами по ломаной 
(рис. 3, справа).
Время распространения сигнала от нижнего зеркала к верхнему и обратно есть разность показаний синхронизированных часов: в точке 
в момент прихода сигнала и в точке в момент его отправления. Обозначим это время через 
.
За время сигнал проходит путь 
, равный 
, а вагон — путь 
. По теореме Пифагора имеем: 
или
.
Умножаем это равенство на 4:
.
С учётом (1) получим:
Отсюда можно выразить через :
. (2)
Полученная формула (2) носит совершенно общий характер. Пусть имеются две системы отсчёта 
и 
, причём система движется относительно K со скоростью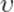 
. Рассмотрим два события, которые в системе происходят в одной точке пространства. Время между этими событиями в системе называется собственным временем. По часам системы между этими событиями проходит время 
, которое связано с собственным временем соотношением (2).
Обратите внимание, что в формуле (2) собственное время делится на величину, меньшую единицы; поэтому всегда выполнено неравенство 
. При этом время оказывается тем больше, чем с большей скоростью система движется относительно .
Данный эффект — так называемое релятивистское замедление времени — оказывается весьма существенным при скоростях, близких к скорости света. Давайте вернёмся к нашему примеру с пассажиром, подбрасывающим яблоко в вагоне. Предположим, что вагон движется со скоростью 
, а время полёта яблока по часам пассажира равно 
с. Тогда на земле между подбрасыванием яблока и его ловлей пройдёт время
Ну а теперь представьте, что с Земли отправляется звездолёт со скоростью 
. Космическое путешествие длится 10 лет по часам астронавтов. Вернувшись на Землю, астронавты обнаруживают, что попали в совершенно иную эпоху — ведь по земным часам прошло 224 года!
Звучит фантастично, но никакой фантастики тут нет — мы имеем дело со строгими фактами теории относительности. Ни с чем подобным нам сталкиваться не доводилось по той причине, что мы не умеем пока перемещаться с околосветовыми скоростями. Но как только эти скорости будут достигнуты, станет реальностью и машина времени для путешествий в будущее:-)