При выводе формулы (2) мы неявно предполагали, что расстояние  между зеркалами одинаково как в вагоне, так и на земле. Но так ли это на самом деле? Да, это действительно так: вертикальные размеры предметов являются одними и те же как в вагонной, так и в земной системе отсчёта.
между зеркалами одинаково как в вагоне, так и на земле. Но так ли это на самом деле? Да, это действительно так: вертикальные размеры предметов являются одними и те же как в вагонной, так и в земной системе отсчёта.
Чтобы убедиться в этом, давайте возьмём два одинаковых вертикальных стержня; один из них поместим в вагон, а другой оставим на земле. Оба стержня пусть будут на одной и той же высоте над землёй. Когда стержни поравняются друг с другом, концы одного стержня сделают засечки на другом стержне. Так вот, из принципа относительности следует, что эти засечки должны прийтись в точности на концы другого стержня.
В самом деле, пусть по засечкам оказывается, например, что вагонный стержень короче земного, т. е. движущийся стержень короче покоящегося. Но по принципу относительности инерциальные системы отсчёта полностью равноправны. Давайте перейдём в систему отсчёта вагона: там вагонный стержень будет покоиться, а земной — двигаться. Тогда получится, что движущийся стержень длиннее покоящегося. Противоречие!
Итак, поперечные размеры предметов одинаковы как в покоящейся, так и в движущейся системе отсчёта. Иначе обстоит дело с продольными размерами.
Вновь вернёмся к нашему вагону и рассмотрим стержень  , расположенный вдоль вектора скорости вагона (рис. 4; изображать вагон надобности уже нет). Стержень, таким образом, двигается со скоростью v параллельно оси
, расположенный вдоль вектора скорости вагона (рис. 4; изображать вагон надобности уже нет). Стержень, таким образом, двигается со скоростью v параллельно оси 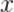 .
.
| Рис. 4. Длина стержня относительна |
Пусть 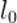 — длина неподвижного стержня, измеренная в вагоне. Она называется собственной длиной стержня. Через
— длина неподвижного стержня, измеренная в вагоне. Она называется собственной длиной стержня. Через  обозначим длину движущегося стержня, измеренную на земле.
обозначим длину движущегося стержня, измеренную на земле.
Для нахождения соотношения между  и
и 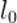 рассмотрим два события: 1) прохождение точки
рассмотрим два события: 1) прохождение точки  мимо фиксированной точки
мимо фиксированной точки  на оси
на оси 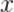 ; 2) прохождение точки
; 2) прохождение точки  мимо точки
мимо точки  .
.
В земной системе отсчёта наши события происходят в одной точке  . Промежуток времени между этими событиями по земным часам пусть равен
. Промежуток времени между этими событиями по земным часам пусть равен  (это собственное время, разделяющее данные события). Очевидно, что
(это собственное время, разделяющее данные события). Очевидно, что
 . (3)
. (3)
В системе отсчёта вагона указанные события происходят в двух различных точках  и
и  . Промежуток времени между этими событиями по вагонным часам равен
. Промежуток времени между этими событиями по вагонным часам равен  . Аналогично имеем:
. Аналогично имеем:
 . (4)
. (4)
Приравнивая правые части формул (3) и (4), получим:
 .
.
Но в силу формулы (2) имеем:
.
Отсюда получаем окончательную формулу:
 . (5)
. (5)
Как видим, собственная длина 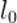 умножается на величину, меньшую единицы; стало быть, длина движущегося стержня будет меньше длины покоящегося стержня. Это так называемое лоренцево сокращение — все тела сокращают размеры в направлении своего движения.
умножается на величину, меньшую единицы; стало быть, длина движущегося стержня будет меньше длины покоящегося стержня. Это так называемое лоренцево сокращение — все тела сокращают размеры в направлении своего движения.
Подчеркнём ещё раз: длина стержня в системе отсчёта, относительно которой стержень движется, меньше длины этого же стержня в системе отсчёта, относительно которой он покоится. Данный эффект связан лишь с особенностями измерительных процедур, свойственных теории относительности. Никаких реальных «сжатий» в движущемся стержне, разумеется, не происходит.
Преобразования Лоренца
Теперь мы можем вывести формулы, связывающие координаты и время фиксированного события в двух различных инерциальных системах отсчёта.
Пусть снова имеются две системы отсчёта: система  и движущаяся относительно неё система
и движущаяся относительно неё система  (рис. 5). При
(рис. 5). При  начала
начала  и
и  этих систем совпадают.
этих систем совпадают.
| Рис. 5. К выводу преобразований Лоренца |
Рассмотрим некоторое событие 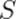 (например, вспышку света). В системе
(например, вспышку света). В системе  это событие происходит в точке с координатами
это событие происходит в точке с координатами  в момент времени
в момент времени  . В системе
. В системе  это же событие происходит в точке с координатами
это же событие происходит в точке с координатами  в момент времени
в момент времени 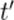 .
.
Как мы уже выяснили, поперечные размеры тел в обеих системах отсчёта одни и те же. Поэтому имеем:  ,
,  .
.
Пусть  — проекция точки
— проекция точки 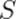 на общую ось абсцисс. Найдём длину отрезка
на общую ось абсцисс. Найдём длину отрезка  в системах
в системах  и
и  .
.
В системе  отрезок
отрезок  покоится. Его длина равна
покоится. Его длина равна 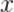 — это собственная длина данного отрезка. В системе
— это собственная длина данного отрезка. В системе  отрезок
отрезок  движется со скоростью
движется со скоростью 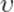 , и его длина в силу формулы (5) равна
, и его длина в силу формулы (5) равна  . Но с другой стороны, в системе
. Но с другой стороны, в системе  длина
длина  равна
равна  . Следовательно,
. Следовательно,
 . (6)
. (6)
Теперь аналогично найдём длину отрезка 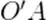 в системах
в системах  и
и  .
.
В системе  отрезок
отрезок 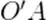 покоится, его собственная длина равна
покоится, его собственная длина равна 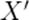 . В системе
. В системе  отрезок
отрезок 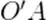 движется со скоростью
движется со скоростью 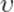 , и его длина равна
, и его длина равна 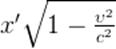 . С другой стороны, длина
. С другой стороны, длина 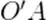 в системе
в системе  равна
равна  . Поэтому
. Поэтому
 . (7)
. (7)
Из формулы (7) выразим 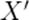 . Полученное выражение подставим в (6) и выразим оттуда
. Полученное выражение подставим в (6) и выразим оттуда 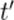 . В результате получим:
. В результате получим:
,  ,
,  ,. (8)
,. (8)
Формулы (8) называются преобразованиями Лоренца. Они дают искомую связь координат и времени события 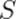 в инерциальных системах отсчёта
в инерциальных системах отсчёта  и
и  . Эти релятивистские формулы, вытекающие из принципов СТО, служат заменой классическим преобразованиям Галилея, опирающимся на представления о мгновенности распространения взаимодействий.
. Эти релятивистские формулы, вытекающие из принципов СТО, служат заменой классическим преобразованиям Галилея, опирающимся на представления о мгновенности распространения взаимодействий.
При малых скоростях движения, т. е. при 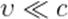 , мы можем считать отношение
, мы можем считать отношение  равным нулю. Тогда преобразования Лоренца переходят в соотношения:
равным нулю. Тогда преобразования Лоренца переходят в соотношения:
 ,
,  ,
,  ,
,  . (9)
. (9)
Эти формулы есть не что иное, как преобразования Галилея. Мы видим, что преобразования Галилея служат предельным случаем преобразований Лоренца, когда скорости тел малы по сравнению со скоростью света. Поэтому при малых скоростях движения релятивистская механика Эйнштейна переходит в классическую механику Ньютона.
С системой равеств (6) и (7) можно поступить иначе. Выразим 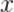 из (6), подставим в (7) и выразим оттуда
из (6), подставим в (7) и выразим оттуда  . В результате придём к другому варианту записи преобразований Лоренца:
. В результате придём к другому варианту записи преобразований Лоренца:
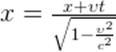 ,
,  ,
,  ,. (10)
,. (10)
Формулы (8) задают переход из системы 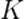 в систему
в систему  . Формулы (10) задают обратный переход из системы
. Формулы (10) задают обратный переход из системы  в систему
в систему 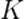 .
.
В предельном случае 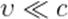 преобразования Лоренца (10) также переходят в преобразования Галилея:
преобразования Лоренца (10) также переходят в преобразования Галилея:
 ,
,  ,
,  ,
,  . (11)
. (11)
Эти формулы, как легко видеть, полностью совпадают с формулами (9).