Устойчивое и неустойчивое равновесие
Разрушение стержня может произойти не только потому, что будет нарушена прочность, но и оттого, что стержень не сохранит той формы, которая ему придана конструктором.
В конструкциях и сооружениях большое применение находят детали, являющиеся относительно длинными и тонкими стержнями, у которых размеры поперечного сечения малы по сравнению с длиной стержня.
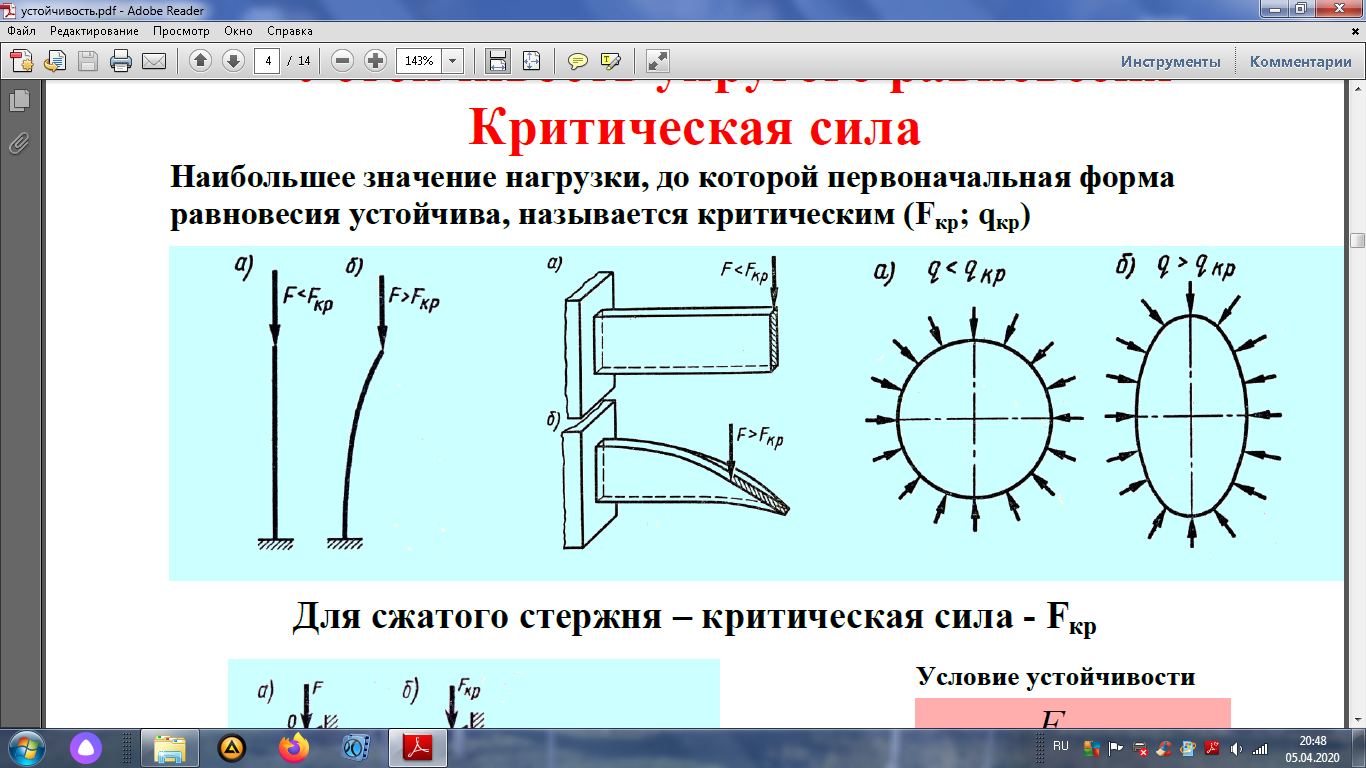
| Поведение таких стержней под действием осевой сжимающей нагрузки оказывается принципиально иным, чем при сжатии коротких стержней: при достижении сжимающей силой F некоторой критической величины, равной Fкр, прямолинейная форма равновесия длинного стержня оказывается неустойчивой, и при превышении Fкр стержень начинает интенсивно искривляется (выпучивается). Это явление носит название потери устойчивости. Потери устойчивости при сжатии длинного стержня носит название продольный изгиб. Равновесие может быть устойчивое и неустойчивое. |
Устойчивость – способность тела сохранять положение или форму равновесия при внешних воздействиях.
Устойчивое равновесие – равновесие, при котором, после снятия внешней отклоняющей силы, стержень восстановит первоначальную форму.
Неустойчивое равновесие – равновесие, при котором стержень под действием сжимающей силы изогнется и в исходное состояние не возвратится.
На устойчивость влияет сжимающая сила.
Критическая сила (Fкр) – нагрузка, превышение которой вызывает потерю устойчивости первоначальной формы (положения) тела.
Расчет на устойчивость
Расчет на устойчивость заключается в определении допускаемой сжимающей силы и в сравнении с ней силы действующей.
F ≤ [F]
[F] =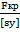 
F ≤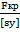
F – действующая сжимающая сила
[F] – допускаемая сжимающая сила, обеспечивает некоторый запас устойчивости
Fкр – критическая сила
[sу] – допускаемый коэффициент запаса устойчивости
Для стали 1,8-3, для чугуна 5, для дерева 2,8
Критическая сила
Критическая сила (при потере устойчивости в упругой стадии) вычисляется по формуле Эйлера
Для шарнирно закрепленного с обоих сторон стержня формула имеет вид:
Fкр =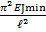 
Е – модуль упругости
Jmin - минимальный осевой момент инерции
ℓ - длина стержня
|
Экспериментальные исследования показали, что Fкр зависит только от способа закрепления стержня. Поэтому оказалось возможным формулу Эйлера распространить на другие способы закрепления концов стержня, заменив ℓ на ℓприведенное.
ℓприв = μ·ℓ,
μ – коэффициент приведения длины, зависит от способа закрепления.
Формула определения критической силы для всех случаев закрепления
Fкр =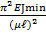 
Критические напряжения
При осевом нагружении стержня в поперечном сечении возникает нормальное напряжение сжатия.
Критическое напряжение соответствует критической силе.
Ϭкр =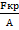 
= 
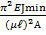
Введем понятие і2 – минимальный радиус инерции
і2min =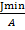 
Тогда формула для расчета критического напряжения перепишется
Ϭкр =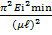 
Отношение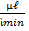 
носит название гибкости стержня - λ.
Гибкость стержня – величина безразмерная, чем больше гибкость, тем меньше напряжение.
Гибкость стержня характеризует способность стержня сопротивляться потере устойчивости при продольном изгибе.
λ =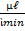 
| гибкость не зависит от материала, а определяется геометрией стержня |
Ϭкр =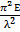 
| |
Формула Эйлера выполняется только в пределах упругих деформаций. (после снятия нагрузки стержень возвращается в первоначальное состояние).
Критическое напряжение должно быть меньше предела упругости.
σкр ≤ σупр
В расчетах предел упругости заменяют пределом пропорциональности σ упр ≈ σпц
Ϭкр = 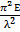≤ Ϭпц
Откуда гибкость стержня λ ≥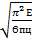 
Предельная гибкость определится λпред ≥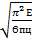
|
Предельная гибкость зависит от материала стержня.
Формула Эйлера применима при λ ≥ λпред.
Многие материалы имеют гибкость меньше предельной.
Разработка методов расчета таких стержней проведена Ясинским.
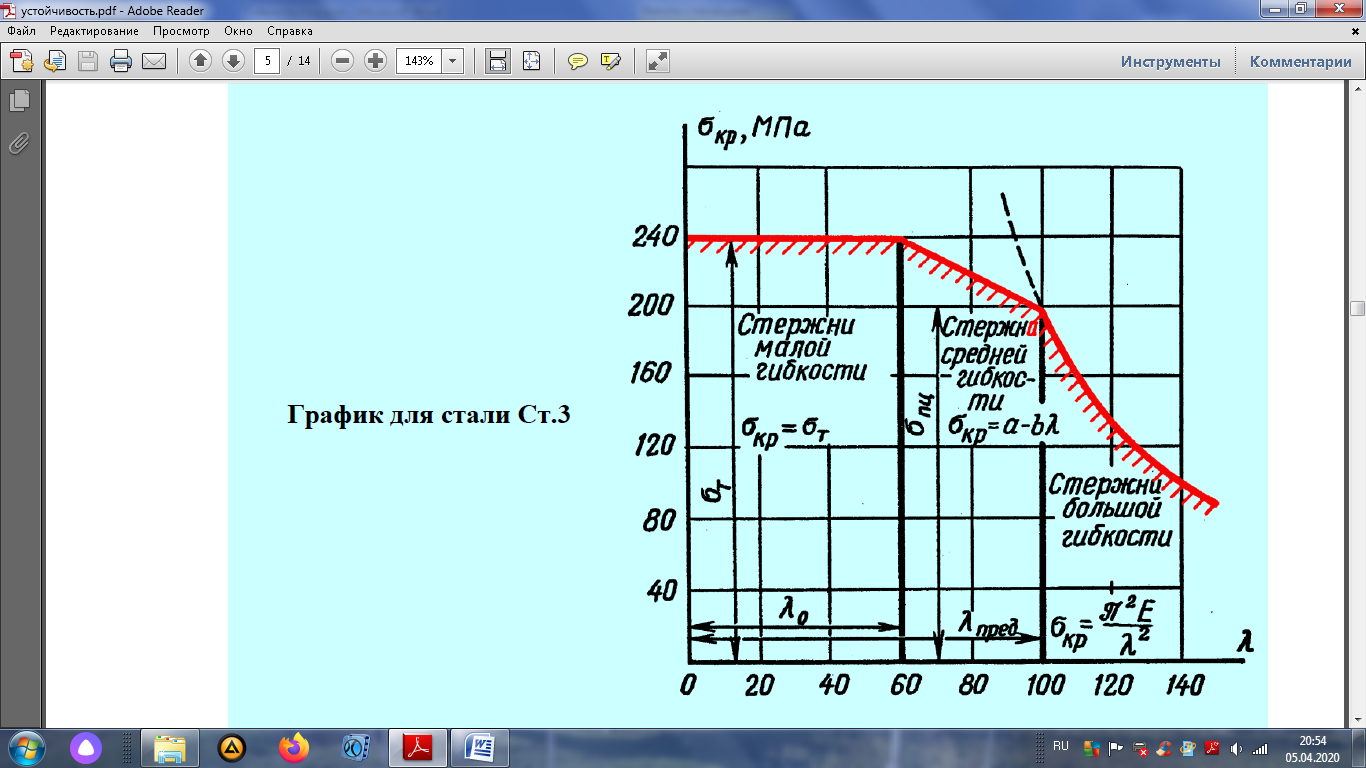
| Условно стержни делят на 3 группы: - малой гибкости, - средней гибкости, - большой гибкости |
График для Ст 3
Проектный расчет заключается в определении минимального осевого момента инерции поперечного сечения стержня по формуле:
Imin = F[sy](μl)2 / (π2E),
где: F - действующая нагрузка; [sy] – допускаемый коэффициент запаса устойчивости; μ – коэффициент приведения длины стержня; l – длина стержня; Е – модуль продольной упругости.
Далее находят гибкость стержня по формуле: λ = μl / imin,
где: imin = √(Imin / A), (А – площадь сечения стержня).
Полученную гибкость сравнивают с предельной для данного материала.
Проверочный расчет заключается в определении действительного коэффициента запаса устойчивости sy и сравнении его с допускаемым:
sy = Fкр / F ≥ [sy].
Силовой расчет заключается в определении допускаемой нагрузки [F] по формуле:
[F] = Fкр / [sy].
Расчет сжатых стержней на устойчивость можно свести к расчету на простое сжатие. При расчете применяют следующую формулу:
[F] = φ[σс]A,
где: [σс] – допускаемое напряжение на сжатие; φ – коэффициент продольного изгиба (справочная величина, определяемая по таблицам).
Расчеты показывают, что при продольном изгибе наиболее выгодными являются кольцевые сечения, имеющие относительно большой момент инерции