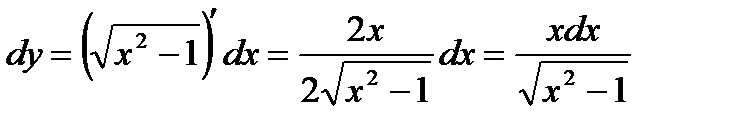Тема занятия
Производная функции, физический и геометрический смысл. Производная сложной функции. Дифференциал функции
Основные понятия и термины по теме: производная функции, геометрический смысл производной, физический смысл производной, правила дифференцирования, производная сложной функции.
План изучения темы
1. Производная функции.
2. Геометрический смысл производной.
3. Физический смысл производной.
4. Основные правила дифференцирования.
5. Производная сложной функции.
6. Дифференциал функции
Производной функции 
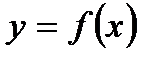в точке 
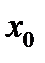называется предел отношения приращения этой функции к приращению аргумента, при условии, что приращение аргумента стремится к нулю.
Производную функции 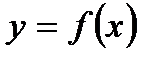в точке 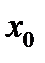обозначают символом 
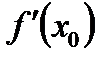или 
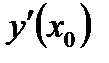. Следовательно, по определению
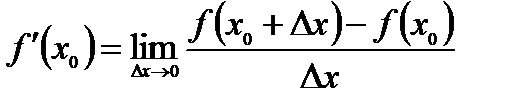или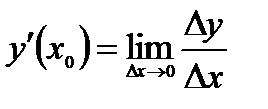 
Геометрический смысл производной.
Производная функци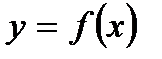и 
при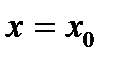 
равна угловому коэффициенту касательной к графику данной функции в точке 
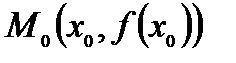, т.е.
,
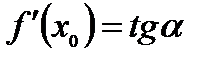где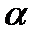 
- угол наклона касательной к оси 
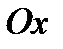прямоугольной декартовой системы координат.
Физический смысл производной.
Если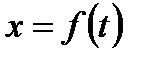 
- законпрямолинейного движения точки, то 
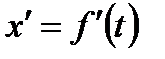- скорость этого движения в момент времени 
.
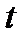Функция, имеющая производную в данной точке, называется дифференцируемой в этой точке. Операция нахождения производной называется дифференцированием.
Основные правила дифференцирования
Теорема: Производная суммы (разности) двух дифференцируемых функции равна сумме (разности) производных этих функций:
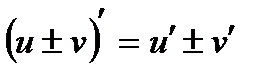
Теорема: Производная произведения двух дифференцируемых функций равна произведению первой функции на производную второй плюс произведению второй функции на производную первой, т.е.:
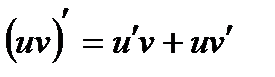
Следствие: Постоянный множитель можно выносить за знак производной:
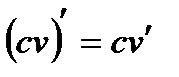
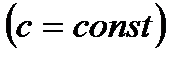
Теорема: Производная частного двух дифференцируемых функций определяется формулой:
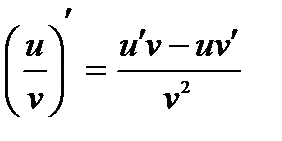
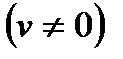
Производная сложной функции:
Теорема: Есл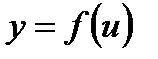и 
и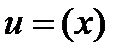 
- дифференцируемые функции своих аргументов, то производная сложной функции 
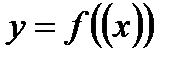существует и равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной, т.е.:
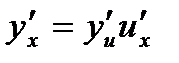
Пример:
Найти производную функции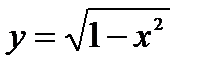 
.
Считая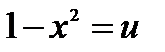 
и применяя формулу получаем 
,
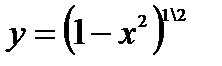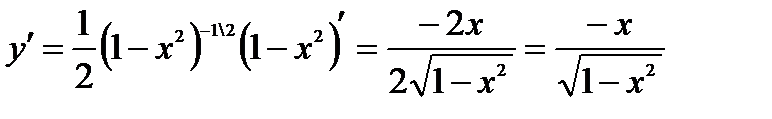
Пример:
Найти производную функции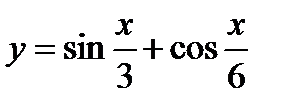 
.
Применяя формулы находим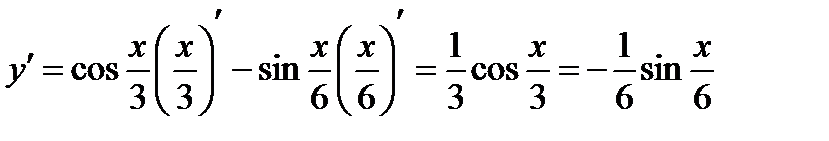 
Пример:
Найти производную функции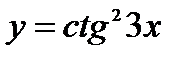 
.
Так как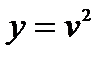 
, где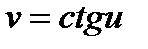 
, 
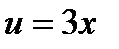, то формулу применяем дважды на основании формул получаем
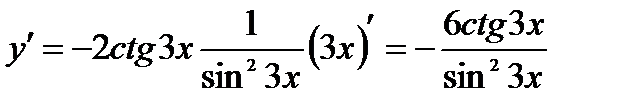
Пример:
Найти производную функции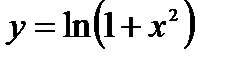 
Применяя таблицу производных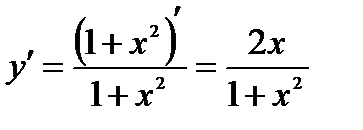 
Дифференциалом функции 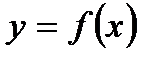(или дифференциалом первого порядка) называется произведение производной этой функции 
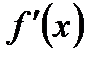на произвольное приращение аргумента 
:
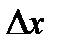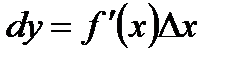
Дифференциал аргумента равен приращению аргумента: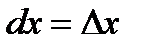 
. Поэтому дифференциал функции равен произведению ее производной на дифференциал аргумента:
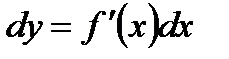.Дифференциалом второго порядка называется дифференциал от дифференциала первого порядка:
,
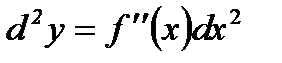дифференциал второго порядка функции 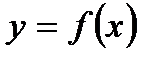равен произведению второй производной этой функции на квадрат дифференциала аргумента.
Геометрический смысл дифференциала функции.
Дифференциал функции 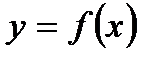в точке х равен приращению ординаты касательной к графику функции в этой точке, когда х получит приращение .
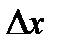Свойства дифференциала функции.
1. Дифференциал суммы дифференцируемых функций равен сумме дифференциалов слагаемых:
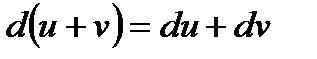
2. Дифференциал произведения двух дифференцируемых функций равен произведению первой функции на дифференциал второй плюс произведение второй на дифференциал первой:
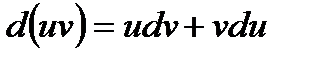
3. Дифференциал частного двух дифференцируемых функций определяется формулой:
, 
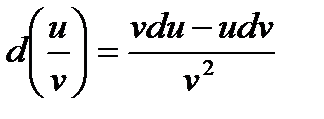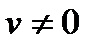
Пример:
Найти дифференциалы функций
1. 
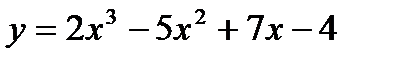
2. 
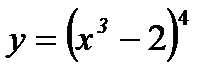
3. 
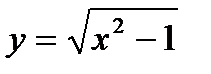
Решение:
1. 
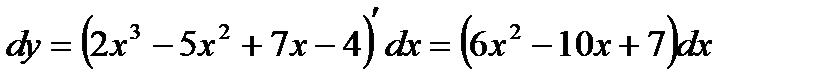
2. 
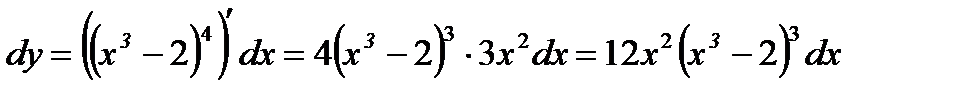
3. 