Теорему Пифагора?
- Квадрат длины гипотенузы прямоугольного треугольника равен сумме квадратов катетов.
- Спасибо, Вася.
- Книга рекордов Гиннеса называет теорему Пифагора теоремой с максимальным числом доказательств. И поясняет: в 1940 году была опубликована книга, которая содержала триста семьдесят доказательств теоремы Пифагора. Электроник – мальчик из чемоданчика в книге Евгения Велтистова знал целых двенадцать способов, среди них «метод укладки паркета» и «стул невесты». Кто-нибудь смотрел фильм приключения Электроника? Советую посмотреть…
Это замечательный фильм о дружбе и ссоре, о правде и лжи, о порядочности и преданности. А какое музыкальное сопровождение!
Теорема Пифагора занимала умы математиков с древнейших времен.
В этом с ней не может тягаться ни одна другая теорема. Всё это говорит о чрезвычайной важности этой теоремы для математики.
Доказательство
Для самого простого доказательства теоремы Пифагора для прямоугольного треугольника нужно задать идеальные условия: пусть треугольник будет не только прямоугольным, но и равнобедренным. Есть основания полагать, что именно такой треугольник первоначально рассматривали математики древности.
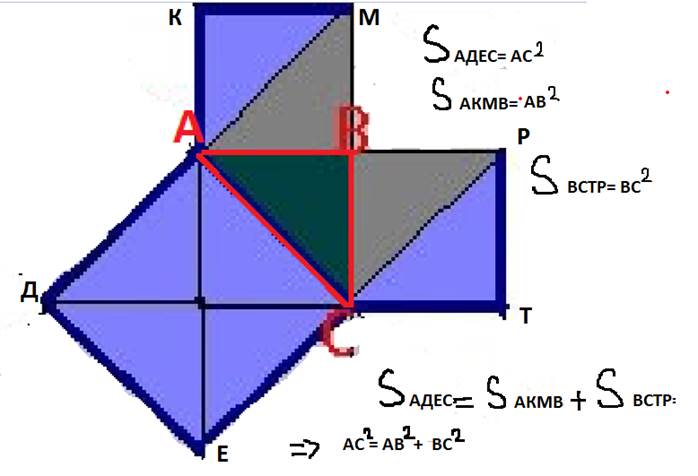
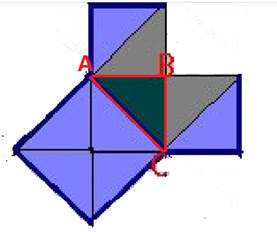
Посмотрите на равнобедренный прямоугольный треугольник ABC.
На гипотенузе АС можно построить квадрат, состоящий из четырех треугольников, равных исходному треугольнику АВС.
А на катетах АВ и ВС построим по квадрату, каждый из которых содержит по два аналогичных треугольника.
То есть «квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на его катетах»
Кстати, этот чертеж лег в основу многочисленных анекдотов и карикатур, посвященных теореме Пифагора. Самый знаменитый, пожалуй, это «Пифагоровы штаны во все стороны равны»:

Пару слов о Пифагоровых тройках
Этот вопрос мало или вообще не изучается в школьной программе. А между тем он является очень интересным и имеет большое значение в геометрии. Пифагоровы тройки применяются для решения многих математических задач. Представление о них может пригодиться вам в дальнейшем.
Так что же такое Пифагоровы тройки? Так называют натуральные числа, собранные по трое, сумма квадратов двух из которых равна третьему числу в квадрате.
Пифагоровы тройки могут быть:
· примитивными (все три числа – взаимно простые);
· не примитивными (если каждое число тройки умножить на одно и то же число, получится новая тройка, которая не является примитивной).
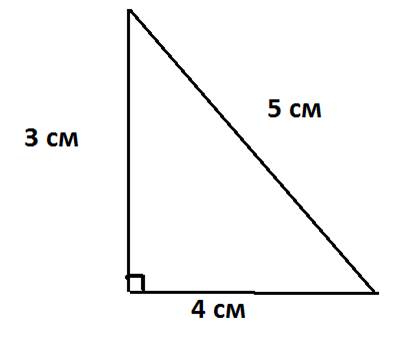
Еще до нашей эры древних египтян завораживала мания чисел Пифагоровых троек: в задачах они рассматривали прямоугольный треугольник со сторонами 3,4 и 5 единиц. К слову, любой треугольник, стороны которого равны числам из пифагоровой тройки, по умолчанию является прямоугольным.
Примеры Пифагоровых троек: (3, 4, 5), (6, 8, 10), (5, 12, 13), (9, 12, 15), (8, 15, 17), (12, 16, 20), (15, 20, 25), (7, 24, 25), (10, 24, 26), (20, 21, 29), (18, 24, 30), (10, 30, 34), (21, 28, 35), (12, 35, 37), (15, 36, 39), (24, 32, 40), (9, 40, 41), (27, 36, 45), (14, 48, 50), (30, 40, 50) и т.д.
Теорема Пифагора находит применение не только в математике, но и в архитектуре и строительстве, астрономии и даже литературе.
С помощью теоремы можно вычислить длину стропила для двускатной крыши. Определить, какой высоты вышка мобильной связи нужна, чтобы сигнал достигал определенного населенного пункта. И даже устойчиво установить новогоднюю елку на городской площади. Как видите, эта теорема живёт не только на страницах учебников, но и часто бывает полезна в реальной жизни.
Что касается литературы, то теорема Пифагора вдохновляла писателей со времен античности и продолжает это делать в наше время. Например, немецкого писателя девятнадцатого века Адельберта фон Шамиссо она вдохновила на написание сонета:
 ….
….

И в заключении хочу добавить:
Пифагор жил в шестом веке до нашей эры, имел красивую внешность, длинную бороду, а на голове золотую диадему.
Пифагор- это не имя, а прозвище, которое философ получил за то, что говорил верно и убедительно, как греческий оракул.
Своими речами приобрёл 2000 учеников, которые образовали свою школу- государство, где действовали законы и правила Пифагора.
Слово “ философ”, как и слово “ космос” достались нам от Пифагора. Он утверждал, что для понимания Бога, человека и природы надо изучить алгебру с геометрией, музыку и астрономию.
Кстати, треугольник- это “ключ” ко всем зашифрованным явлениям нашей жизни. Всё в природе разделено на три части.
“Узрите треугольник - и любая проблема на две трети решена ”.
Когда в задаче просят найти отрезок или угол, я ищу треугольник, в котором они расположены. И именно благодаря этому действию, я научился решать задачи по геометрии. Чего и вам желаю.
Спасибо за внимание))))
Материалы:
1 Цитата на доске
2. Чертежи

Портрет Пифагора
