МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РФ
Федеральное государственное бюджетное образовательное учреждение высшего образования
«ПЕНЗЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
ПЕДАГОГИЧЕСКИЙ ИНСТИТУТ ИМ В.Г.БЕЛИНСКОГО
Факультет физико- математических и естественных наук
Кафедра «Информатика и методика преподавания информатике и математике»
Направление подготовки - 44.03.01 Педагогическое образование
Профиль подготовки - Математика
Исследовательская работа на тему:
«Теорема Менелая и теорема Чевы»
Выполнила студентка группы 16ФПМ1:
Борисова Анна Андреевна
Руководитель: к.п.н, доцент
Марина Елена Владимировна
Пенза, 2020
Содержание
Введение. 2
Глава 1. Теоретические основы по теме «Теорема Менелая и теорема Чевы». 6
1.1. Теорема Менелая. 7
1.2. Теорема Чевы.. 10
Джовани Чева (1648-1734) – итальянский инженер-гидравлик и экономист. Носящая его имя теорема содержится в опубликованной им в 1678г. работе «О прямых линиях». 10
Глава 2. Задачи на применение теорем Менелая и Чевы.. 13
Заключение. 23
Список литературы.. 25
Введение
Геометрия - одна из наиболее древних математических наук.
Первые геометрические факты мы находим в вавилонских клинописных таблицах и египетских папирусах.
Возникновение геометрических знаний связано с практической деятельностью людей. И уже в древности геометрия превратилась в дедуктивную, строго логическую науку, построенную на основе системы аксиом. Постепенно развиваясь, она обогащалась новыми теоремами, идеями, методами. Интересы геометров и направление их научных исследований порою менялись в процессе исторического развития этой науки, поэтому, нелегко дать точное и исчерпывающее определение, что такое геометрия сегодня, каков её предмет, содержание и методы.
В III в. до н. э. древнегреческий учёный Евклид написал книгу под названием «Начала». В этой книге Евклид подытожил накопленные к тому времени геометрические знания и попытался дать законченное аксиоматическое изложение этой науки. Написана она была настолько хорошо, что в течение 2000 лет всюду преподавание геометрии велось либо по переводам, либо по незначительным переработкам книги Евклида.
Например, таким пособием был учебник А. Д. Александрова, затем А.П. Киселёва, по которым советская школа работала до середины 20 столетия.
Но жизнь идёт своим чередом, издаются новые учебники, под редакцией А.В. Погорелова; Л. С. Атанасяна, И.М. Смирнова и др.
В результате различных преобразований со страниц этих учебников как – то незаметно исчезли многие замечательные утверждения, свойства, которые просто необходимо знать при решении многих планиметрических задач.
Обучаясь в Научном Обществе Гимназии и работая с различной дополнительной литературой по геометрии, я столкнулся с тем, что в действительности многие удивительные соотношения и изящные геометрические факты не входят в основной курс геометрии. Многие из них сейчас выглядят малоинтересными, несовершенными и встречаются только в энциклопедиях. Однако некоторые из них продолжают жить, и по сей день. Одни из них теоремы Менелая и Чевы. Это теорема, которая была доказана древнегреческим математиком и астрономом Менелаем Александрийским, жившим в I веке до нашей эры и теорема, опубликованная в 1678 году итальянским математиком и инженером Джованни Чевой. В честь этих учёных теоремы названы их именами.
Эти теоремы просты, интересны и находят применение при решении как простых, так и весьма сложных задач. Несмотря на это Теоремы Менелая и Чевы не изучаются в школе на уроках геометрии и встречаются только в школьном учебнике геометрии под редакцией Атанасяна Л.С. в приложении. Доказательства, предложенные автором сложны. Задачи, помещённые в учебнике на применение обратной теоремы Менелая трудны, а задачи на применение прямой теоремы вовсе не рассматриваются.
Актуальность темы:
v Данная тема является дополнением и углублением изученных в курсе геометрии свойств.
v Применение опыта решения планиметрических задач с использованием теоремы Чевы и Менелая помогает повысить уровень пространственного воображения и уровень логической культуры.
v Изучение данной темы поможет более глубоко подготовиться к вступительным экзаменам и олимпиадам.
v Хорошо известно, что выводы школьной геометрии находят широкое применение при решении самых разнообразных практических задач. Знание геометрии необходимо всем кому приходиться исследовать свойства различных фигур и тел. Геометрия изучает наш реальный мир.
Цель работы:
ü ознакомление с теоремами Чевы и Менелая;
ü исследование способов доказательства теорем;
ü овладение приемами решений планиметрических задач с использованием теоремы Чевы и Менелая;
ü систематизация и обобщение теоретического и практического материалов.
Задачи исследования:
§ изучить состояние проблемы в научной литературе и школьной программе;
§ выявить теоретические положения для доказательства теорем;
§ систематизировать теоретический материал доказательств:
а) Теоремы Чевы,
б) Теоремы Менелая;
§ проверить эффективность и целесообразность применения теорем при решении задач;
§ научиться применять теоремы Чевы и Менелая в задачах разной сложности;
§ сравнить задачи, решенные с использованием теорем Менелая и Чевы с задачами, решенными традиционным способом;
Теоремы Чевы и Менелая можно назвать «двойственными» они, похоже, формулируются и доказываются. В своей работе я предлагаю доказательства теоремы Менелая (прямая и обратная), используя подобия треугольников, а теорему Чевы доказываю с помощью теоремы Менелая.
Однако при решении целого класса задач эти теоремы позволяют легко и изящно получить решение, в то время когда традиционные подходы приводят к громоздким и утомительным преобразованиям.
Глава 1. Теоретические основы по теме «Теорема Менелая и теорема Чевы»
Переходя к основной части работы, я начну с замечательных точек треугольника. К числу таких точек, изучаемых в школьном курсе геометрии, относятся:
а) точка пересечения биссектрис (центр вписанной окружности), которая
находится внутри треугольника;
б) точка пересечения серединных перпендикуляров (центр описанной
окружности), которая может находится внутри (остроугольный треугольник),
вне треугольника (тупоугольный треугольник) или в вершине прямого угла
прямоугольного треугольника;
в) точка пересечения высот (ортоцентр). Для остроугольного треугольника
ортоцентр находится внутри треугольника, а в тупоугольном – вне.
г) точка пересечения медиан (центроид), которая находится внутри треугольника.
Тот факт, что, каждая из троек данных отрезков пересекаются в одной точке, я докажу позже.
Теорема Менелая
Теорема названа в честь древнегреческого учёного Менелая (I в. н.э.), которая была им доказана и опубликована в третей книге «Сферики». Долгое время её называли «теоремой о секущих».
Теорема Менелая. Если прямая пересекает стороныили продолжения сторон BC, CA и AB треугольника ABC соответственно в точках A1 , B1 и C1, не совпадающие с вершинами треугольника, то имеет место равенство
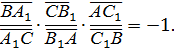
| C |
| A1 |
| C1 |
| B |
| A |
| B1 |
| D |
Пусть прямая пересекает стороны BC и CA треугольника АВС в точках А1 и В1 ,а продолжение стороны АВ в точке С1.
Через вершину С треугольника АВС проведем прямую CD 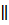 АВ; которая пересечет прямую А1В1 в точке D.
АВ; которая пересечет прямую А1В1 в точке D.
1.  А1ВС1
А1ВС1 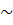
 А1CD по двум углам
А1CD по двум углам
2.  В1АС1
В1АС1 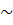
 В1CD по двум углам
В1CD по двум углам
3. из пунктов 2 и 3 следует, что  и
и  .
.
5. Перемножим эти равенства, получим доказываемое соотношение.
Доказательство остается в силе и в том случае, когда все три точки A1, B1 и C1 лежат на продолжениях сторон  АВС.
АВС.
Для пояснения приведённого доказательства сделаем одно уточнение. Пусть 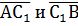 – ненулевые коллинеарные векторы. Если
– ненулевые коллинеарные векторы. Если 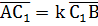 , то будем писать:
, то будем писать: 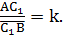 Значит, число k равно отношению длин векторов
Значит, число k равно отношению длин векторов 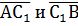 , взятому со знаком «плюс», если векторы сонаправленны, и со знаком «минус», если они направлены противоположно.
, взятому со знаком «плюс», если векторы сонаправленны, и со знаком «минус», если они направлены противоположно.
Легко проверить, что при таком соглашении полученное выше равенство принимает вид:

Обратная теорема. Если выполняется равенство 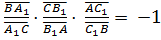 , то точки A1, B1 и C1 лежат на одной прямой.
, то точки A1, B1 и C1 лежат на одной прямой.
Для доказательства обратной теоремы используем вышеуказанное уточнение
Доказательство.
Допустим, что выполнено равенство  , и пусть прямая А1В1 пересекает прямую АВ в точке С2. Согласно прямой теореме,
, и пусть прямая А1В1 пересекает прямую АВ в точке С2. Согласно прямой теореме,

Сравнивая это соотношение с данным, заключаем, что 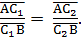
Прибавив к обеим частям равенства 1, получим: 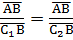 откуда
откуда 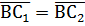 , т. е. точки C1 и C2 совпадают.
, т. е. точки C1 и C2 совпадают.
Объединяя прямую и обратную теоремы, получаем следующий результат.
Если на сторонах ВС, СА, АВ треугольника АВС или на их продолжениях взяты точки A1 , B1 и C1, то эти точки лежат на одной прямой тогда и только тогда, когда

ЗАМЕЧАНИЕ. При решении задач, когда расположение точек A1, B1 и C1 известно равенство используют в скалярном виде, т. е. рассматривают длины отрезков, а правую часть равенства берут равной 1.
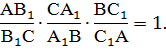
Теорема Чевы
Джовани Чева (1648-1734) – итальянский инженер-гидравлик и экономист. Носящая его имя теорема содержится в опубликованной им в 1678г. работе «О прямых линиях».
Теорема Чевы. Пусть на сторонах ВС, СА, АВ треугольника АВС или их продолжениях взяты соответственно точки А1, В1, С1, не совпадающие с вершинами треугольника. Тогда если прямые АА1, ВВ1, СС1 пересекаются или попарно параллельны, то
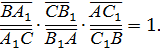
Доказательство.
I) Пусть прямые АА1, ВВ1, СС1 пересекаются в точке О, лежащей внутри или вне треугольника АВС. В том и другом случае, применив теорему Менелая к треугольнику ВСС1 и секущей АА1, Получим:
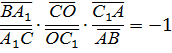
| А |
| С |
| В |
 А1 А1
|
| С1 |
| В1 |
| О |
| О |
| В |
| А |
| С |
 А1 А1
|
| В1 |
| С1 |
| а) |
| б) |
Аналогично из треугольника АСС1, пересеченного прямой ВВ1, находим:
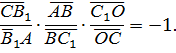
Перемножим последние два равенства
почленно и получим:
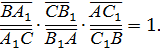
II) Рассмотрим случай, когда прямые АА1, ВВ1, СС1 параллельны. Пусть точка В1 лежит на продолжении стороны АС, точка А1 лежит на стороне ВС, точка С1 лежит на стороне АВ. Тогда достаточно доказать, что
| С1 |
| В1 |
| A |
| С |
| В |
| А |
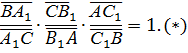
Используя теорему об отрезках, отсекаемых на сторонах угла параллельными прямыми, имеем:

Подставим эти равенства в левую часть формулы (*) имеем:
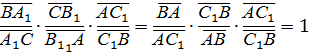
Что и требовалось доказать.
Обратная теорема. Если выполняется равенство  , то прямые AA1, BB1 и CC1 либо пересекаются в одной точке, либо попарно параллельны.
, то прямые AA1, BB1 и CC1 либо пересекаются в одной точке, либо попарно параллельны.
Доказательство.
Предположим теперь, что выполняется равенство (*), и докажем, что тогда прямые АА1, ВВ1, СС1 пересекаются в одной точке. Пусть С2 – Точка пересечения прямой АВ с прямой проходящей через точку С и точку пересечения прямых АА1, ВВ1. Для точки С2 выполняется отношение, как и для точки С1.
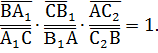
Поэтому,  =
=  . Следовательно, C2 совпадает C1, т. е. прямые AA1, BB1 и CC1 пересекаются в одной точке.
. Следовательно, C2 совпадает C1, т. е. прямые AA1, BB1 и CC1 пересекаются в одной точке.
Замечание. Записывая отношение отрезков, следует двигаться по контуру треугольника от вершины до точки пересечения с прямой и от точки пересечения до следующей вершины.