Как видно из доказательств, они очень похожи, поэтому, при рассмотрении теоретического материала, я рассмотрел сразу обе теоремы. А теперь в практической части попробую доказать свою гипотезу, показав красоту решения некоторых задач с использованием ранее неизвестных мне теорем. И для сравнения покажу решение одной и той же задачи разными способами.
Задача 1. На сторонах АВ и АС  АВС взяты точки M и N так, что
АВС взяты точки M и N так, что  . Отрезки BN и CM пересекаются в точке K. Найдите отношение отрезков
. Отрезки BN и CM пересекаются в точке K. Найдите отношение отрезков 
| A |
| B |
| C |
| M |
| N |
| K |
 и секущей CM. Получим,
и секущей CM. Получим,

| K |



Решение задачи используя подобие треугольников.
1. Проведём прямую BD параллельную стороне АС. Точка D точка пересечения этой прямой с прямой СМ.
2. Рассмотрим треугольники DKB и CKN. Данные треугольники подобны. 

3.  ;
;
4. 


5. 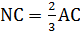 , из условия.
, из условия.
6. 
Ответ: 
Задача разобрана мною двумя способами для сравнения. Краткость решения во втором способе подтверждает моё предположение о необходимости изучения этих теорем в школе. Продолжу:
Теперь докажем известные нам факты о замечательных точках с использованием теоремы Чевы.
| D |
| N |
| A |
| B |
| C |
| M |
| K |
Доказательство:
Пусть АА1, ВВ1, СС1 – биссектрисы треугольника АВС, т.к. биссектриса угла треугольника делит противолежащую сторону на отрезки, длины которых пропорциональны противолежащим сторонам, то
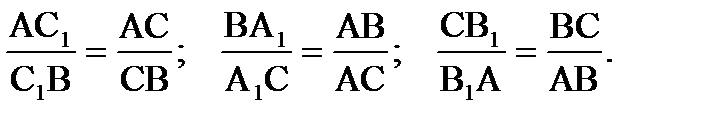 Перемножив полученные равенства, получим:
Перемножив полученные равенства, получим:
 Т.о. по теореме Чевы, биссектрисы пересекаются в одной точке.
Т.о. по теореме Чевы, биссектрисы пересекаются в одной точке.
|
Задача 3: Докажите, что медианы треугольника пересекаются в одной точке.
| А |
| А1 |
| С |
| В |
| С1 |
| В1 |
 Так как ВВ1, СС1, АА1 медианы имеем, что
Так как ВВ1, СС1, АА1 медианы имеем, что Тогда в силу теоремы Чевы прямые ВВ1, СС1, АА1 пересекаются в одной точке. Ч.т.д.
Тогда в силу теоремы Чевы прямые ВВ1, СС1, АА1 пересекаются в одной точке. Ч.т.д.
Школьное доказательство.
Рассмотрим треугольник АВС. Обозначим буквой О точку пересечения медиан АА1 и ВВ1.
Проведём среднюю линию А1В1 этого треугольника.
| А |
| А1 |
| С |
| В |
| С1 |
| В1 |
| О |

Следовательно,  и значит их стороны пропорциональны:
и значит их стороны пропорциональны:

АВ = 2 А1В1, поэтому АО = 2А1О и ВО = 2В1О.
Таким образом, точка О пересечения медиан АА1
и ВВ1делит каждую из них в отношении 2:1,
считая от вершины.
Аналогично доказывается, что точка пересечения
медиан ВВ1 и СС1 делит каждую из них
в отношении 2:1, считая от вершины, и, следовательно, совпадает с точкой О. Итак, все три медианы треугольника АВС пересекаются в одной точке и делятся ею в отношении 2:1, считая с вершины.
Задача 4. Докажите что высоты остроугольного треугольника пересекаются в одной точке.
Доказательство.
Пусть BN,AM,CK высоты треугольника АВС проведённые соответственно к сторонам АС,СВ,АВ.

| N |
| М |
| С |
| В |
| А |
| K |

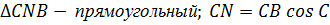



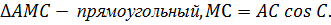

Тогда в силу теоремы Чевы прямые BN, AM, CK пересекаются в одной точке.Ч.т.д.
| О |
| А |
| В |
| С |
| А1 |
| В1 |
| С1 |
| А2 |
| С2 |
| В2 |
Рассмотрим произвольный треугольник АВС и докажем. Что прямые АА1, ВВ1,СС1, содержащие его высоты пересекаются в одной точке.
Проведём через каждую вершину треугольника АВС прямую,параллельную каждой стороне. Получим треугольник А2В2С2.
1. Точки А, В, С середины сторон треугольника АВС. АВ = А2С,
АВ = СВ2как противоположные стороны параллелограмма АВА2С и АВСВ2, поэтому А2С = СВ2.
2. Аналогично С2А = АВ2, С2В = ВА2.
3.  .
.
Таким образом прямые АА1, ВВ1,СС1 являются серединными перпендикулярами к сторонам треугольника А2В2С2.Значит, они пересекаются в одной точке.
Что и требовалось доказать.
Задача 5: Доказать, что прямые, проходящие через вершины треугольника и точки касания вписанной окружности, пересекаются в одной точке, называемой точкой Жергона.
( французский математик Жозеф Диаз Жергон, 1776 – 1831 г.г )
| С |
Доказательство:
Пусть окружность касается сторон треугольника АВС в точках А1, В1, С1, т.к. длины касательных, проведённых из одной точки к окружности, равны, то АВ1=АС1, ВС1=ВА1, СА1=СВ1.
Тогда  Следовательно, по теореме Чевы, данные прямые пересекаются в одной точке.
Следовательно, по теореме Чевы, данные прямые пересекаются в одной точке.
|
| А1 |
| В |
| А |
| В1 |
| С1 |
Задача 6: Докажите, что прямые, проходящие через вершины треугольника и точки касания вневписанных окружностей, пересекаются в одной точке (точке Нагеля).
(немецкий учёный Нагель Христиан Генрих фон (1803-1882 г.г)).
Чтобы доказать данную теорему, необходимо ввести определение вневписанной окружности.
Определение: Окружность называется вневписанной, если она касается одной стороны этого треугольника и продолжений двух других его сторон. Сделаем чертёж. Центр вневписанной окружности, лежит в точке пересечения биссектрис внешних углов треугольника.

Доказательство:
Тогда, из прямоугольных треугольников ОВС1, ОАС1 получим:  ;
;
из прямоугольных треугольников О2В1С, О2АВ1 получим:  ;
;
из прямоугольных треугольников О1ВА1, О1А1С получим: 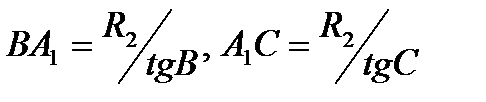 , составим произведение соответствующих отрезков с использованием равенства из теоремы Чева:
, составим произведение соответствующих отрезков с использованием равенства из теоремы Чева:

Т.о. данные прямые пересекаются в одной точке.
Таким образом, мы добавили к замечательным точкам треугольника ещё две: точку Жергонна и точку Нагеля.
Задача 7 (прямая Симпсона). Основания перпендикуляров, проведенных к прямым, содержащим стороны треугольника, из произвольной точки, описанной около него окружности, лежат на одной прямой.
| А |
| В |
| Р |
| С |
| С1 |
| В1 |
| А1 |
Решение. Пусть PA1, PB1, PC1 перпендикуляры, проведённые к прямым, содержащим стороны треугольника АВС. Запишем теорему Менелая для 
 А теперь докажем, что это равенство верно.
А теперь докажем, что это равенство верно.
1) △BBA1- прямоугольный.ВА1=BP ⋅cosPBC 
△PA1C- прямоугольный.CA1=CP⋅cosPCB 
BA1A1C=-PCcosPCAPAcosPAC 
2) △B1PC- прямоугольный.CB1=PCcosPCA 
△ABB1- прямоугольный.AB1=PAcosPAC 
CB1AB1=-APcosPCAPBcosPAC 
3) △AC1P- прямоугольный.AC1=APcosPAB 
△C1BP- прямоугольный.C1B=PBcosPBA 
AC1C1B=-APcosPABPBcosPBA 
4) ∠PAB=∠PCB-т.к.операются на одну дугу 
∠PAC=∠PBC-т.к.операются на одну дугу 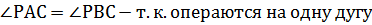
5) ∠PCA+∠PBA=180° 
∠PAC=180°-∠PBA 
cosPBC=cos180°-∠PBA=-cosPBA 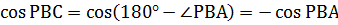
cosPAC=cosPBA=cos180°-∠PCA=-cosPCA 
ВА1А1С⋅СB1B1A⋅AC1C1B=-BPcosPBCCPcosPCB∙-CPcosPCAAPcosPAC∙-APcosPABPBcosPBA=-1 
Следовательно, в силу теоремы Менелая точки А1, В1. С1 лежат на одной прямой.
Задача 8 (Теорема Дезарга). Прямые АА1, ВВ1 , СС1 пересекаются в одной точке О. Докажите, что точки пересечения прямых AB и A1B1, BC и B1C1, AC и A1C1 лежат на одной прямой.
SHAPE \* MERGEFORMAT
| A1 |
| A |
| C1 |
| B2 |
| B1 |
| B |
| A2 |
| C2 |
| С С |
| O |
Решение.
Пусть A2 , B2, C2 – точки пересечения прямых BC и B1C1, AC и A1C1, AB и A1B1. Применим теорему Менелая к следующим треугольникам и секущем:
1) △ОАВ и секщая А1В1: AA1A1O⋅OB1B1B⋅BC2C2A=-1 
2) △ОВСи секщая С1В1: ОС1С1С⋅ВВ1B1О⋅СА2А2В=-1 
3) △ОАС и секщая А1С1: ОА1A1А⋅АB2B2С⋅СC1C1О=-1 
4) Перемножив равенства получим.
AВ2В2С⋅СА2С2А⋅BC2C2A=-1
 Следовательно в силу теоремы Менелая точки А2, В2, С2Лежат на одной прямой.
Следовательно в силу теоремы Менелая точки А2, В2, С2Лежат на одной прямой.
Заключение
Теоремы Чевы и Менелая просты в понимании. Но трудности, связанные с освоением этих теорем, оправданы их применением при решении задач.
Замечательным свойством теорем является то, что они могут служить отправной точкой при повторении основных свойств треугольника в 9 классе. В частности, с их помощью легко доказываются следующие утверждения:
· Медианы треугольника пересекаются в одной точке.
· Высоты треугольника пересекаются в одной точке.
· Биссектрисы внутренних углов треугольника пересекаются в одной точке.
Одним из замечательных свойств геометрических задач является многообразие методов их решения. Поэтому остановимся на том, когда же имеет смысл применять теорему Менелая при решении задач? Возможность применить теоремы Менелая имеет смысл, когда в условии задачи:
1. Идёт речь, об отношении отрезков (иногда завуалированном: доказать равенство отрезков, доказать, что точка является серединой отрезка).
2. Если на чертеже имеются элементы, присутствующие в теореме Менелая (треугольник и прямая, пересекающая его стороны или их продолжения).
3. Иногда полезно применять обратную теорему (если необходимо доказать, что какие-нибудь точки лежат на одной прямой). А также при доказательстве теорем.
В своей работе с помощью теоремы Менелая я доказываю теорему Чевы, Симпсона, Дезарга и многие другие известные соотношения.
Доказательства утверждений приводятся в работе.
Применение опыта решения планиметрических задач с использованием теорем Чевы и Менелая даёт дополнительные возможности при изучении геометрии, помогает повысить уровень пространственного воображения и уровень логической культуры.
Теоремы Чевы и Менелая помогают решить задачи более рационально, чем их решение другими способами, например векторным, которое требует дополнительных действий; быстро и оригинально решить задачи повышенной сложности.
Данная работа содержит геометрический материал достаточный для того, чтобы использовать его на элективных курсах и как дополнительный материал для учащихся интересующихся математикой. Данную работу можно продолжить, изучив применение этих теорем в пространстве.
Список литературы
1. Энциклопедия для детей. Том 11. Математика. М.: Аванта +, 2002.
2. Прасолов В. В. Задачи по планиметрии: Ч.1. М.: Наука, Физматлит, 1995.
3. Сканави М. И. Сборник задач по математике для поступающих во Втузы. М.: Высшая Школа, 1995.
4. Г. С. М. Коксетер, С. Л. Грейтцер. Новые встречи с геометрией. М.: Наука, 1991.
5. Математика. Еженедельное учебно-методическое приложение к газете «Первое сентября», 2004 №13,14.
6. Б.Орач «Теорема Менелая». Квант № 3, 1991.
7. Шарыгин И.Ф. Геометрия. Задачник.9—11 классы. — М.: Дрофа, 1996.
8. К. А. Иванов «О пропорциональных отрезках в треугольнике», журнал «Математика в школе» №8-2004.
9. Е. Качалкина «Применение теорем Чевы и Менелая», журнал «Математика в школе» №13,14 -2004.
10. Г.И.Глейзер. История математики в школе – 1983, - 316с.