| A | B | F |
Логическое умножение КОНЪЮНКЦИЯ - это новое сложное выражение будет истинным только тогда, когда истинны оба исходных простых выражения. Конъюнкция определяет соединение двух логических выражений с помощью союза И.
Обозначается: *, Ù,·,& (читается ampersand ).
| A | B | F |
Логическое сложение – ДИЗЪЮНКЦИЯ - это новое сложное выражение будет истинным тогда и только тогда, когда истинно хотя бы одно из исходных (простых) выражений. Дизъюнкция определяет соединение двух логических выражений с помощью союза ИЛИ
Обозначается: Ú, +, |.
| A | А |
Логическое отрицание: ИНВЕРСИЯ - если исходное выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное выражение ложно, то результат отрицания будет истинным/ Данная операция означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО
Обозначается знаком перед переменной (X), либо чертой сверху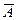 
| A | B | F |
Логическое следование: ИМПЛИКАЦИЯ - связывает два простых логических выражения, из которых первое является условием (А), а второе (В)– следствием из этого условия. Результатом ИМПЛИКАЦИИ является ЛОЖЬ только тогда, когда условие А истинно, а следствие В ложно. Выражается словами ЕСЛИ …, ТО …
Обозначается →
| A | B | F |
Логическая равнозначность: ЭКВИВАЛЕНТНОСТЬ - определяет результат сравнения двух простых логических выражений А и В. Результатом ЭКВИВАЛЕНТНОСТИ является новое логическое выражение, которое будет истинным тогда и только тогда, когда оба исходных выражения одновременно истинны или ложны. Обозначается символом "эквивалентности"
Обозначается <=>
Основные законы логики: А = А – закон тождества
А &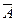 
= 0 – закон непротиворечия
A Ú 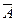= 1 – закон исключенного третьего
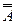= А – закон двойного отрицания
------------------------------------------------------------------------------------------------------------------------------------------------------
Свойства констант: 
= 1 
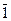= 0
А Ú 0 = А А & 0 = 0
А Ú 1 = 1 А & 1 = 1
------------------------------------------------------------------------------------------------------------------------------------------------------
Законы идемпотентности: А Ú А = А
А & А = A
------------------------------------------------------------------------------------------------------------------------------------------------------
Законы коммутативности: А Ú В = В Ú А
А & В = В & А
------------------------------------------------------------------------------------------------------------------------------------------------------
Законы ассоциативности: А Ú (В Ú С) = (АÚ В) Ú С
А & (В & С) = (А & В) & С
------------------------------------------------------------------------------------------------------------------------------------------------------
Законы дистрибутивности: А Ú (В & С) = (АÚ В) & (А Ú С)
А & (В Ú С) = (А & В) Ú (А& С)
------------------------------------------------------------------------------------------------------------------------------------------------------
Законы поглощения: А Ú (А & В) = А
А & (А Ú В) = А
------------------------------------------------------------------------------------------------------------------------------------------------------
Законы де Моргана: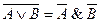 
------------------------------------------------------------------------------------------------------------------------------------------------------
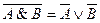
· операцию «импликация» можно выразить через «ИЛИ» и «НЕ»:
A → B = A Ú B или в других обозначениях A → B =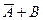 
Порядок выполнения логических операций в сложном логическом выражении:
1. инверсия
2. конъюнкция
3. дизъюнкция
4. импликация
5. эквивалентность
Количество строк = 2n + две строки для заголовка (n - количество переменных)
Количество столбцов = количество переменных + количество логических операций
| n | 2n |
Операции над множествами рассматриваются для получения новых множеств из уже существующих.
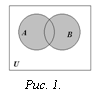Определение. Объединением множеств А и В называется множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множеств А, В (рис. 1):
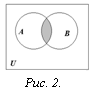
Определение. Пересечением множеств А и В называется множество, состоящее из всех тех и только тех элементов, которые принадлежат одновременно как множеству А, так и множеству В (рис. 2):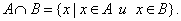 
Определение. Разностью множеств А и В называется множество всех тех и только тех элементов А, которые не содержатся в В (рис. 3): 