1. Приготовьте таблицу для записи результатов измерений и вычислений.
2. Измерьте длину узкой трубки l и выразите объем воздуха в ней в условных единицах объема (пусть каждый миллиметр длины трубки соответствует единице объема). Давление воздуха в трубке равно атмосферному. Определите его по барометру.
3. Погрузите трубку в сосуд с горячей водой. Через 1–2 мин воздух в трубке прогреется до температуры воды. Характерным признаком равенства температур воды и воздуха в трубке будет прекращение выделения воздушных пузырьков из нижнего конца погруженной в воду трубки. Измерьте температуру воды. Результаты измерений объема, давления и температуры, выраженной в единицах абсолютной шкалы, запишите в таблицу.
| Состояние газа | p, мм рт. ст. | V, усл. ед. | Т, °С | Т, К |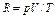 
|
4. Выньте трубку из горячей воды и погрузите в сосуд с холодной водой открытым концом вниз. При погружении температура воздуха в трубке, ее объем и давление изменятся.
5. Спустя 1–2 мин измерьте температуру холодной воды и объем воздуха в трубке. Чтобы определить давление воздуха в этом состоянии, следует к атмосферному давлению прибавить давление столба воды, которое определяется его высотой h от поверхности воды до ее уровня в трубке. Давление следует выразить в миллиметрах ртутного столба. (Давление 1 мм рт. ст. равно давлению 13,6 мм вод. ст.) Поэтому 
, где h выражено в миллиметрах. Температуру выразите в единицах абсолютной шкалы. Результаты измерений запишите в таблицу.
6. Выньте трубку из холодной воды, вытряхните из нее воду. Так как за время проведения эксперимента горячая вода несколько остыла, проведите опыт еще раз для других значений температуры.
7. Для каждого состояния вычислите произведение давления на объем, деленное на температуру.
8. Определите относительную и абсолютную погрешности, последнюю сравните с разностью полученных результатов.
Контрольные вопросы
1. результаты вычислений величины, приведенной в последней графе таблицы, оказались неодинаковыми. При каком условии это не противоречит утверждению о ее постоянстве?
2. Укажите погрешности, ухудшающие результат, которые трудно учесть при выполнении работы.
Лабораторная работа №5-III
Оценка средней скорости
теплового движения молекул газа
Цель работы: оценить среднюю скорость теплового движения молекул газа по реактивному действию газовой струи, принимая, что молекулы газа вылетают из сосуда с этой скоростью.
Оборудование: пластмассовый баллон из-под шампуня, штатив, резиновая пробка со шлангом, весы, гири, насос, манометр, линейка демонстрационная длиной 2,5 м.
Содержание и метод выполнения работы
Одно из основных свойств вещества в газообразном состоянии – это способность неограниченно расширяться и занимать любой предоставленный ему объем. Используя способность газа к неограниченному расширению, можно оценить приблизительно скорость теплового движения его молекул.
Если в сосуде, заполненном газом, имеется отверстие, то молекулы газа будут вылетать из него с теми самыми скоростями, с какими они движутся внутри сосуда. Можно считать, что скорость истечения газовой струи из сосуда в вакууме примерно равна средней скорости теплового движения молекул.
Истечение газовой струи приводит к возникновению реактивной силы. Если сосуд не связан с другими телами, то в результате истечения газа он, как ракета, движется в противоположном направлении. По закону сохранения импульса можно записать:
,
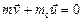где m – масса газа, вышедшего из сосуда, 
– скорость истечения газовой струи, m c – масса баллона,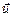 
– скорость движения баллона.
Для оценки скорости v истечения газовой струи нужно измерить начальную скорость u движения сосуда-«ракеты», его массу m c и массу m газа:
. (1)
В качестве сосуда можно взять пластмассовую бутылку из-под шампуня. Бутылку следует насадить на резиновую пробку с отверстием с таким усилием, чтобы она слетала с пробки при избыточном давлении около 105 Па.
Пробку с помощью шлангов соединяют с насосом и манометром, закрепляют пробку в лапке штатива и насаживают на нее пластмассовую бутылку (см. рисунок). Накачивая воздух в бутылку, постепенно повышают давление в ней. Когда бутылка взлетает вертикально вверх, из нее выходит воздух до тех пор, пока давление оставшегося в ней воздуха не понизится до атмосферного. Массу m выходящего из «ракеты» воздуха можно найти из уравнения Клайперона – Менделеева:
, (2)
где 
– избыточное давление воздуха в сосуде, измеренное манометром, V – объем бутылки, M – молярная масса газа, Т – его температура.
Отсюда масса m вышедшего воздуха равна:
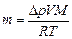. (3)
Начальную скорость u «ракеты» можно найти по высоте ее подъема:
. (4)