1. Определить массы всех образцов.
2. При помощи мензурки налить в калориметр 70 мл холодной воды. Измерить её температуру.
3. Получить у преподавателя нагретый до 100 °С образец №1 (железо), опустить его в калориметр, дождаться установки теплового равновесия, измерить температуру воды.
4. Вычислить значение удельной теплоёмкости образца.
5. Аналогичным образом поступить с образцами №2, 3, 4 (Al, Pb, Ti).
6. Построить график с (М).
7. Рассчитать теплоемкость С каждого образца, сравнить эти значения.
8. По этим данным найти универсальную газовую постоянную R и постоянную Больцмана k.
9. Для образца №5 (Cu) найти молярную массу (массу атома).
Обратите внимание на то, что по определению атомной единицы массы (а.е.м.) масса атома в а.е.м. равна массе моля вещества в граммах, а в системе СИ основной единицей массы является килограмм.
Постоянная Авогадро Na = 6,022×1023 1/моль.
Лабораторная работа №7-IV
Определение модуля Юнга для стальной струны
Цель работы: изучить характер изменения удлинения стальной струны при изменении силы растяжения; определить модуль Юнга.
Оборудование:прибор для изучения деформации растяжения с индикатором малых перемещений, гиря известной массы, стальная струна, микрометр, ученическая линейка.
Содержание и метод выполнения работы
Напряжение. В любом сечении деформированного тела действуют силы упругости, препятствующие разрыву тела на части (рис. 1).
Рис. 1
Состояние деформированного тела характеризуют особой величиной, называемой напряжением или, точнее, механическим напряжением. Напряжение – величина, равная отношению модуля F силы упругости к площади поперечного сечения S тела:
s = F / S. (1)
В СИ за единицу напряжения принимается 1 Па = 1 Н/м2.
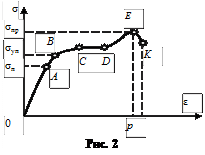Диаграмма растяжения. Для исследования деформации растяжения стержень из исследуемого материала при помощи специальных устройств подвергают растяжению и измеряют удлинение образца и возникающее в нём напряжение. По результатам опытов вычерчивают график зависимости напряжения s от относительного удлинения e, получивший название диаграммы растяжения (рис. 2).
Закон Гука. Опыт показывает, что при малых деформациях напряжение s прямо пропорционально относительному удлинению e (участок ОА диаграммы). Эта зависимость, называемая законом Гука, записывается так:
s = Е |e|. (2)
Относительное удлинение e в формуле (2) взято по модулю, так как закон Гука справедлив как для деформации растяжения, так и для деформации сжатия, когда e < 0.
Коэффициент пропорциональности Е, входящий в закон Гука, называется модулем упругости или модулем Юнга.
Если относительное удлинение e = 1, то e = Е. Следовательно, модуль Юнга равен напряжению, возникающему в стержне при его относительном удлинении, равном 1. Так как e = D l / l 0, то D l = l 0 при e = 1. А это значит, что модуль Юнга равен напряжению, возникающему при удвоении длины образца. Практически любое тело при упругой деформации не может удвоить свою длину. Значительно раньше любой стержень разорвётся. Поэтому модуль Юнга определяют по формуле (2), измеряя напряжение s и относительное удлинение e при малых деформациях.
Для большинства широко распространённых материалов модуль Юнга определён экспериментально. Так, для хромоникелевой стали Е = 2,1×1011 Па, а для алюминия Е = 7×107 Па. Чем больше Е, тем меньше деформируется стержень при прочих равных условиях (одинаковых F, S, l 0). Модуль Юнга характеризует сопротивляемость материала упругой деформации растяжения (сжатия).
Закон Гука, записанный в форме (2), легко привести к виду, известному из курса физики. Действительно, подставив в (2) s = F / S и e = | D l | / l 0, получим
Отсюда
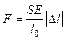. (3)
Обозначим 
, тогда
. (4)
Таким образом, жёсткость k стержня прямо пропорциональна произведению модуля Юнга на площадь поперечного сечения стержня и обратно пропорциональна его длине.
Если увеличивать нагрузку, то деформация становится нелинейной: напряжение перестаёт быть прямо пропорциональным относительному удлинению. Тем не менее, при небольших нелинейных деформациях после снятия нагрузки форма и размеры тела практически восстанавливаются (участок АВ диаграммы). Максимальное напряжение, при котором ещё не возникают заметные остаточные деформации, (относительная остаточная деформация не превышает 0,1%), называют пределом упругости sуп.
Предел прочности. Если внешняя нагрузка такова, что напряжение в материале превышает предел упругости, то после снятия нагрузки образец хотя и укорачивается, но не принимает прежних размеров, а остаётся деформированным.
По мере увеличения нагрузки деформация нарастает всё быстрее и быстрее. При некотором значении напряжения, соответствующем на диаграмме точке С, удлинение нарастает практически без увеличения нагрузки. Это явление называют текучестью материала (участок СD). Кривая на диаграмме идёт при этом почти горизонтально.
Далее с увеличением деформации e кривая напряжений начинает немного возрастать и достигает максимума в точке Е. Затем напряжение быстро спадает и образец разрушается (точка К). Таким образом, разрыв происходит после того, как напряжение достигает максимального значения sпч, называемого пределом прочности (образец растягивается без увеличения внешней нагрузки вплоть до разрушения). Эта величина зависит от материала образца и от метода его обработки.