Подготовительная часть. В часы самоподготовки курсанты повторяют содержание материала лекции. При этом особое внимание уделяется уяснению следующих положений:
1) устройство компьютера и принцип его работы;
2) основные блоки в IBM PC;
5) системы счисления;
6) двоичная арифметика;
7) единицы измерения информации.
В тетради сделать запись темы и целей занятия, кратких теоретических сведений по отрабатываемым учебным вопросам.
Элементы теории
Система счисления – это способ записи чисел с помощью заданного набора специальных знаков (цифр).
Существуют позиционные и непозиционные системы счисления.
В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число. Например, в числе 757,7 первая семерка означает 7 сотен, вторая – 7 единиц, а третья – 7 десятых долей единицы.
Сама же запись числа 757,7 означает сокращенную запись выражения
700 + 50 + 7 + 0,7 = 7•102 + 5•101 + 7•100 + 7•10-1 = 757,7.
Любая позиционная система счисления характеризуется своим основанием.
Основание позиционной системы счисления – это количество различных знаков или символов, используемых для изображения цифр в данной системе.
За основание системы можно принять любое натуральное число – два, три, четыре и т.д. Следовательно, возможно бесчисленное множество позиционных систем: двоичная, троичная, четверичная и т.д. Запись чисел в каждой из систем счисления с основанием q означает сокращенную запись выражения
an-1 qn-1 + an-2 qn-2+... + a1 q1 + a0 q0 + a-1 q-1 +... + a-m q-m,
где ai – цифры системы счисления; n и m – число целых и дробных разрядов, соответственно.
Кроме десятичной широко используются системы с основанием, являющимся целой степенью числа 2, а именно:
· двоичная (используются цифры 0, 1);
· восьмеричная (используются цифры 0, 1,..., 7);
· шестнадцатеричная (для первых целых чисел от нуля до девяти используются цифры 0, 1,..., 9, а для следующих чисел - от десяти до пятнадцати – в качестве цифр используются символы A, B, C, D, E, F).
Пример 1:

Из всех систем счисления особенно проста и поэтому интересна для технической реализации в компьютерах двоичная система счисления. Компьютеры используют двоичную систему потому, что она имеет ряд преимуществ перед другими системами:
· для её реализации нужны технические устройства с двумя устойчивыми состояниями (есть ток – нет тока, намагничен – не намагничен и т.п.), а не, например, с десятью, – как в десятичной;
· представление информации посредством только двух состояний надежно и помехоустойчиво;
· возможно применение аппарата булевой алгебры для выполнения логических преобразований информации;
· двоичная арифметика намного проще десятичной.
Недостаток двоичной системы – быстрый рост числа разрядов, необходимых для записи чисел.
Полезно запомнить запись в представленных системах счисления первых двух десятков целых чисел:
| 10 - я | 2 - я | 8 - я | 16 - я | 10 - я | 2 - я | 8 - я | 16 - я |
| A | |||||||
| B | |||||||
| C | |||||||
| D | |||||||
| E | |||||||
| F | |||||||
Особенности использования восьмеричной и шестнадцатеричной
систем счисления
Двоичная система, удобная для компьютеров, для человека неудобна из-за ее громоздкости и непривычной записи.
Перевод чисел из десятичной системы в двоичную и наоборот выполняет машина. Однако, чтобы профессионально использовать компьютер, следует научиться понимать слово машины. Для этого и разработаны восьмеричная и шестнадцатеричная системы.
Числа в этих системах читаются почти так же легко, как десятичные, требуют соответственно в три (восьмеричная) и в четыре (шестнадцатеричная) раза меньше разрядов, чем в двоичной системе (ведь числа 8 и 16 – соответственно, третья и четвертая степени числа 2).
Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему очень прост: достаточно каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр) или тетрадой (четверкой цифр).
Пример 2:

Чтобы перевести число из двоичной системы в восьмеричную или шестнадцатеричную, его нужно разбить влево и вправо от запятой на триады (для восьмеричной) или тетрады (для шестнадцатеричной) и каждую такую группу заменить соответствующей восьмеричной (шестнадцатеричной) цифрой.
Пример 3:

Перевод целых чисел из десятичной системы в любую другую позиционную систему счисления
При переводе целого десятичного числа в систему с основанием q его необходимо последовательно делить на q до тех пор, пока не останется остаток, меньший или равный q–1. Число в системе с основанием q записывается как последовательность остатков от деления, записанных в обратном порядке, начиная с последнего.
Пример 4: Перевести число 75 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:
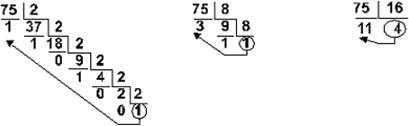
Ответ: 7510 = 1 001 0112 = 1138 = 4B16.
Двоичная арифметика
Правило сложения двух чисел в двоичной системе счисления:
1) сложение чисел производится поразрядно, начиная с младшего разряда, с использованием таблицы сложения для двоичной системы счисления (табл. 1);
2) при сложении цифр в каждом разряде необходимо добавлять к их сумме единицы переноса из младших разрядов.
Для умножения чисел в позиционной системе счисления с любым основанием следует умножить множимое на каждый разряд множителя и просуммировать частные произведения, сдвинутые друг относительно друга на один разряд. Таблица умножения для двоичной системы счисления приведена в табл. 2.
Таблица 1
| Сложение + | 1-ое слагаемое | 2-ое слагаемое | результат |
|
1 11 1
+ 1001, 012
 1101, 112
1101, 112
1 0111, 002
Таблица 2
| Умножение X | множимое | множитель | результат |
Пример 6.
x 10012
11012
|
 1001
1001
 1001
1001
11101012
Вопросы и задания для самопроверки
1. В чём заключается принцип открытой архитектуры.
2. Перечислите и укажите назначение периферийных устройств компьютера.
3. Виды памяти ПК.
4. Двоичная, восьмеричная, десятичная, шестнадцатеричная системы счисления. Правила перевода из одной системы счисления в другую.
5. Поясните порядок сложения и умножения двоичных чисел.
6. Единицы измерения информации. Связь байта с Кб, Мб, Гб.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ