С о к р а т. Говорили мне те из жрецов и жриц, которым не все равно, сумеют ли они или не сумеют дать ответ насчет того, чем они занимаются. О том же говорит и Пиндар, и многие другие божественные поэты. А говорят они вот что (смотри, правда ли это): они утверждают, что душа человека бессмертна, и, хотя она то перестает существовать - это и называют смертью, - то снова рождается, она никогда не гибнет (22). Поэтому и следует прожить жизнь как можно более благочестиво:
Кто Персефоне пеню воздаст
За все, чем встарь он был отягчен,
Души тех на девятый год
К солнцу, горящему в вышине,
Вновь она возвратит.
Из них возрастут великие славой цари
И полные силы кипучей и мудрости вящей мужи, -
Имя чистых героев им люди навек нарекут.
А раз душа бессмертна, часто рождается и видела все и здесь, и в Аиде, то нет ничего такого, чего бы она не познала; поэтому ничего удивительного нет в том, что и насчет добродетели, и насчет всего прочего она способна вспомнить (23) то, что прежде ей было известно. И раз все в природе друг другу родственно, а душа все познала, ничто не мешает тому, кто вспомнил что-нибудь одно, - люди называют это познанием, - самому найти и все остальное, если только он будет мужествен и неутомим в поисках: ведь искать и познавать - это как раз и значит припоминать. Выходит, не стоит следовать твоему доводу, достойному завзятых спорщиков: он сделает всех нас ленивыми, он приятен для слуха людей изнеженных, а та речь заставит нас быть деятельными и пытливыми. И, веря в истинность этой речи, я хочу вместе с тобой поискать, что такое добродетель.
М е н о н. Ладно, Сократ. Только как это ты говоришь, что мы ничего не познаем, а то, что мы называем познанием, есть припоминание? Можешь ты меня убедить в том, что это именно так?
С о к р а т. Я и раньше говорил, что ты, Менон, ловкач. Вот сейчас ты спрашиваешь, могу ли я тебя убедить, хотя я утверждаю, что существует не убеждение, а припоминание; видно, ты желаешь уличить меня в том, что я сам себе противоречу.
М е н о н. Нет, клянусь Зевсом, Сократ, я не ради этого сказал так, а только по привычке. Но если ты можешь показать мне, что это так, как ты говоришь, - покажи.
С о к р а т. Это нелегко, но ради тебя, так и быть, постараюсь. Позови-ка мне из твоей многочисленной челяди кого-нибудь одного, кого хочешь, чтобы я на нем мог тебе все показать.
М е н о н. С удовольствием. Подойди-ка сюда!
С о к р а т. Он грек? И говорит по-гречески?
М е н о н. Конечно: ведь он родился в моем доме.
С о к р а т. А теперь внимательно смотри, что будет: сам ли он станет вспоминать или научится от меня.
М е н о н. Смотрю внимательно.
С о к р а т. Скажи мне, мальчик, знаешь ли ты, что квадрат таков?
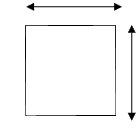
Р а б. Знаю (23а).
С о к р а т. Значит, у этой квадратной фигуры все ее стороны равны, а числом их четыре?
Р а б. Да.
С о к р а т. А не равны ли между собой также линии, проходящие через центр?
Р а б. Равны.
С о к р а т. А не могла бы такая же фигура быть больше или меньше, чем эта?

Р а б. Могла бы.
С о к р а т. Так вот если бы эта сторона была в два фута и та в два фута, то сколько было бы футов во всем квадрате? Заметь только вот что. Если бы эта сторона была в два фута, а та - в один, разве всего в нем было бы не два фута?
Р а б. Два.
С о к р а т. А когда и та сторона будет равна двум футам, разве не получится у нас дважды по два фута?
Р а б. Получится.
С о к р а т. Значит, [в этом квадрате] будет дважды по два фута?
Р а б. Верно.
С о к р а т. А сколько же это будет - дважды два фута? Посчитай и скажи!
Р а б. Четыре, Сократ.
С о к р а т. А может быть фигура вдвое больше этой, но все же такая, чтобы у нее, как и у этой, все стороны были между собою равны?
Р а б. Может.
С о к р а т. Сколько же в ней будет футов?
Р а б. Восемь.
С о к р а т. Ну, а теперь попробуй-ка сказать, какой длины у нее будет каждая сторона. У этой они имеют по два фута, а у той, что будет вдвое больше?
Р а б. Ясно, Сократ, что вдвое длиннее.
С о к р а т. Видишь, Менон, я ничего ему не внушаю, а только спрашиваю. И вот теперь он думает, будто знает, какие стороны образуют восьмифутовыи квадрат. Или, по-твоему, это не так?
М е н о н. Так.
С о к р а т. Что же, знает он это?
М е н о н. Вовсе не знает!
С о к р а т. Но думает, что такой квадрат образуют вдвое увеличенные стороны?
М е н о н. Да.
С о к р а т. Теперь смотри, как он сейчас вспомнит одно за другим все, что следует вспомнить. {К мальчику} А ты скажи мне вот что. По-твоему, выходит, что, если удвоить стороны, получается удвоенный квадрат? Я имею в виду не такую фигуру, у которой одна сторона длинная, а другая короткая, а такую, у которой все четыре стороны равны, как у этой, - но только удвоенную, восьмифутовую. Вот и посмотри: тебе все еще кажется, что ее образуют удвоенные стоны?
Р а б. Да, кажется.
С о к р а т. А разве не выйдет у нас сторона вдвое больше этой, если мы, продолжив ее, добавим еще одну, точно такую же?
Р а б. Выйдет.
С о к р а т. Значит, по-твоему, если этих больших сторон будет четыре, то получится восьмифутовый квадрат?
Р а б. Получится.
С о к р а т. Пририсуем-ка к этой еще три, точно такие же стороны. Неужели, по-твоему, это и есть восьмифутовый квадрат?
Р а б. Ну конечно.
С о к р а т. А разве не будет в нем четырех квадратов, каждый из которых равен этому, четырехфутовому?

Р а б. Будет.
С о к р а т. Выходит, какой же он величины? Не в четыре ли раза он больше первого?
Р а б. Как же иначе?
С о к р а т. Что же он, сразу и в четыре, и в два раза больше первого?
Р а б. Нет, клянусь Зевсом!
С о к р а т. Во сколько же раз он больше?
Р а б. В четыре.
С о к р а т. Значит, благодаря удвоению сторон получается площадь не в два, а в четыре раза большая?
Р а б. Твоя правда.
С о к р а т. А четырежды четыре - шестнадцать, не так ли?
Р а б. Так.
С о к р а т. Из каких же сторон получается восьмифутовый [квадрат]? Ведь из таких вот получился [квадрат], в четыре раза больший?
Р а б. И я так говорю.
С о к р а т. А из сторон вдвое меньших - четырехфутовый [квадрат]?
Р а б. Ну да.
С о к р а т. Ладно. А разве восьмифутовый [квадрат] не равен двум таким вот [маленьким квадратам] или половине этого [большого квадрата]?
Р а б. Конечно, равен.
С о к р а т. Значит, стороны, из которых он получится, будут меньше этой большой стороны, но больше той маленькой.
Р а б. Мне кажется, так.
С о к р а т. Очень хорошо; как тебе покажется, так и отвечай. Но скажи-ка мне: ведь в этой линии - два фута, а в этой - четыре, верно?
Р а б. Верно.
С о к р а т. Значит, сторона восьмифутовой фигуры непременно должна быть больше двух и меньше четырех футов?
Р а б. Непременно.
С о к р а т. А попробуй сказать, сколько в такой стороне, по-твоему, будет футов?
Р а б. Три фута.
С о к р а т. Если она должна иметь три фута, то не надо ли нам прихватить половину вот этой [двухфутовой] стороны, - тогда и выйдет три фута? Здесь - два фута, да отсюда один; и с другой стороны так же: здесь - два фута и один отсюда. Вот и получится фигура, о которой ты говоришь. Не так ли?
Р а б. Так.
С о к р а т. Но если у нее одна сторона в три фута и другая тоже, не будет ли во всей фигуре трижды три фута?
Р а б. Очевидно, так.
С о к р а т. А трижды три фута - это сколько?
Р а б. Девять.
С о к р а т. А наш удвоенный квадрат сколько должен иметь футов, ты знаешь?
Р а б. Восемь.
С о к р а т. Вот и не получился у нас из трехфутовых сторон восьмифутовый квадрат.
Р а б. Не получился.
С о к р а т. Но из каких же получится? Попробуй сказать нам точно. И если не хочешь считать, то покажи.
Р а б. Нет, Сократ, клянусь Зевсом, не знаю.
С о к р а т. Замечаешь, Менон, до каких пор он дошел уже в припоминании? Сперва он, так же как теперь, не знал, как велика сторона восьмифутового квадрата, но думал при этом, что знает, отвечал уверенно, так, словно знает, и ему даже в голову не приходила мысль о каком-нибудь затруднении. А сейчас он понимает, что это ему не под силу, и уж если не знает, то и думает, что не знает.
М е н о н. Твоя правда.
С о к р а т. И разве не лучше теперь обстоит у него дело с тем, чего он не знает?
М е н о н. По-моему, лучше.
С о к р а т. Так разве мы нанесли ему хоть какой-нибудь вред, запутав его и поразив оцепенением, словно скаты?
М е н о н. По-моему, ничуть.
С о к р а т. Значит, судя по всему, мы чем-то ему помогли разобраться, как обстоит дело? Ведь теперь, не зная, он с удовольствием станет искать ответа, а раньше он, беседуя с людьми, нередко мог с легкостью подумать, будто говорит правильно, утверждая, что удвоенный квадрат должен иметь стороны вдвое более длинные.
М е н о н. Да, похоже, что так.
С о к р а т. Что же, по-твоему, он, не зная, но думая, что знает, принялся бы искать или изучать это - до того, как запутался, и, поняв, что не знает, захотел узнать?
М е н о н. По-моему, нет, Сократ.
С о к р а т. Значит, оцепенение ему на пользу?
М е н о н. Я думаю.
С о к р а т. Смотри же, как он выпутается из этого затруднения, ища ответ вместе со мной, причем я буду только задавать вопросы и ничему не стану учить его. Будь начеку и следи, не поймаешь ли меня на том, что я его учу и растолковываю ему что-нибудь, вместо того чтобы спрашивать его мнение. [К мальчику.] А ты скажи мне: не это ли у нас четырехфутовый квадрат? Понимаешь?
Р а б. Это.
С о к р а т. А другой, равный ему квадрат мы можем к нему присоединить?
Р а б. Конечно.
С о к р а т. А еще третий, равный каждому из них?
Р а б. Конечно.
С о к р а т. А вот этот угол мы можем заполнить, добавив точно такой же квадрат?
Р а б. Ну а как же?
С о к р а т. И тогда получатся у нас четыре равные фигуры?

Р а б. Получатся.
С о к р а т. Дальше. Во сколько раз всё вместе будет больше первого квадрата?
Р а б. В четыре.
С о к р а т. А нам нужно было получить квадрат в два раза больший, помнишь?
Р а б. Помню.
С о к р а т. Вот эта линия, проведенная из угла в угол, разве она не делит каждый квадрат пополам?
Р а б. Делит.
С о к р а т. Так разве не получатся у нас четыре равные между собой стороны, образующие вот этот [новый] квадрат?
Р а б. Верно.
С о к р а т. А теперь посмотри, какой величины он будет.
Р а б. Не знаю.
С о к р а т. Но разве каждый из четырех [малых] квадратов не разделен такой линией пополам? Так или нет?
Р а б. Разделен.
С о к р а т. Сколько же таких [треугольных] половинок будет в этом [новом] квадрате?
Р а б. Четыре.
С о к р а т. А в этом [маленьком]?
Р а б. Две.
С о к р а т. А во сколько раз четыре больше двух?
Р а б. Вдвое.
С о к р а т. Во сколько же футов у нас получился квадрат?
Р а б. В восемь футов.
С о к р а т. А из каких сторон?
Р а б. Вот из этих.
С о к р а т. Ведь это - линии, проведенные в [малых] квадратах из угла в угол?
Р а б. Ну да.
С о к р а т. Люди ученые называют такую линию диагональю. Так что если ей имя - диагональ, то ты, Менонов раб, утверждаешь, что эти диагонали образуют наш удвоенный квадрат.
Р а б. Так оно и есть, Сократ (24).
С о к р а т. Ну, как по-твоему, Менон? Сказал он в ответ хоть что-нибудь, что не было бы его собственным мнением?
М е н о н. Нет, все его собственные.
С о к р а т. А ведь он ничего не знал, мы сами говорили об этом только что.
М е н о н. Твоя правда.
С о к р а т. Значит, эти мнения были в нем самом, не так ли?
М е н о н. Так.
С о к р а т. Получается, что в человеке, который не знает чего-нибудь, живут верные мнения насчет того, чего он не знает?
М е н о н. Видимо, так.
С о к р а т. Теперь эти мнения зашевелились в нем, словно сны. А если бы его стали часто и по-разному спрашивать о том же самом, будь уверен, он в конце концов ничуть не хуже других приобрел бы на этот счет точные знания.
М е н о н. Как видно, приобрел бы.
С о к р а т. При этом он все узнает, хотя его будут не учить, а только спрашивать, и знания он найдет в самом себе?
М е н о н. Ну да.
С о к р а т. А ведь найти знания в самом себе - это и значит припомнить, не так ли?
М е н о н. Конечно.
С о к р а т. Значит, то знание, которое у него есть сейчас, он либо когда-то приобрел, либо оно всегда у него было?
М е н о н. Да.
С о к р а т. Если оно всегда у него было, значит, он всегда был знающим, а если он его когда-либо приобрел, то уж никак не в нынешней жизни. Не приобщил же его кто-нибудь к геометрии? Ведь тогда его обучили бы всей геометрии, да и прочим наукам. Но разве его кто-нибудь обучал всему? Тебе это следует знать хотя бы потому, что он родился и воспитывался у тебя в доме.
М е н о н. Да я отлично знаю, что никто его ничему не учил.
С о к р а т. А все-таки есть у него эти мнения или нет?
М е н о н. Само собой, есть, Сократ, ведь это очевидно.
С о к р а т. А если он приобрел их не в нынешней жизни, то разве не ясно, что они появились у него в какие-то иные времена, когда он и выучился [всему]?
М е н о н. И это очевидно.
С о к р а т. Не в те ли времена, когда он не был человеком?
М е н о н. В те самые.
С о к р а т. А поскольку и в то время, когда он уже человек, и тогда, когда он им еще не был, в нем должны жить истинные мнения, которые, если их разбудить вопросами, становятся знаниями, - не все ли время будет сведущей его душа? Ведь ясно, что он все время либо человек, либо не человек.
М е н о н. Разумеется.
С о к р а т. Так если правда обо всем сущем живет у нас в душе, а сама душа бессмертна (25), то не следует ли нам смело пускаться в поиски и припоминать то, чего мы сейчас не знаем, то есть не помним?
М е н о н. Сам не знаю почему, Сократ, но, мне кажется, ты говоришь правильно.
С о к р а т. Мне и самому так кажется, Менон. Впрочем, иные вещи нам особенно отстаивать не придется. А вот за то, что мы, когда стремимся искать неведомое нам, становимся лучше и мужественнее и деятельнее тех, кто полагает, будто неизвестное нельзя найти и незачем искать, - за это я готов воевать, насколько это в моих силах, и словом, и делом.
М е н о н. И это, по-моему, ты очень правильно говоришь, Сократ.