Расчет вала на виброустойчивость по точному методу А. Н. Крылова усложняется, если число сосредоточенных масс (дисков) оказывается больше единицы. В связи с этим в практике химического машиностроения получил распространение так называемый метод приведения, основанный на исследованиях академика Ю. А. Шиманского.
Метод приведения, достаточно точный для инженерных расчетов, позволяет наглядно представить влияние многочисленных факторов на критическую скорость и тем самым способствует рациональному конструированию роторов. Метод базируется на использовании следующих известных формул, которые для удобства вычислений даны в безразмерном виде.
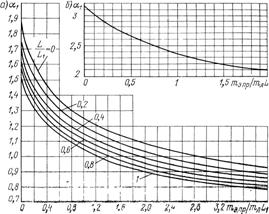
Рисунок 13 - Корни 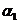 частотного уравнения для вала: а - консольного, б - однопролетного
частотного уравнения для вала: а - консольного, б - однопролетного
Относительный приведенный коэффициент жесткости вала:
консольного (рисунок 14, а, б)
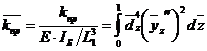 ; (35)
; (35)
однопролетного (рисунок 15, в, г)
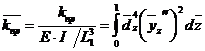 , (36)
, (36)
где 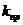 - приведенный коэффициент жесткости вала, Н/м;
- приведенный коэффициент жесткости вала, Н/м;
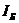 - момент инерции сечения вала на опоре Б, м4;
- момент инерции сечения вала на опоре Б, м4;
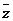 - относительная текущая координата,
- относительная текущая координата, 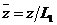 - для консольного вала,
- для консольного вала, 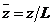 - для однопролетного вала;
- для однопролетного вала;
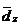 - относительный диаметр вала в точке с координатой z,
- относительный диаметр вала в точке с координатой z, 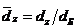 ;
;
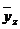 - относительный прогиб вала в точке с координатой z,
- относительный прогиб вала в точке с координатой z, 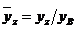 ; (здесь
; (здесь 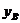 - прогиб вала в точке приведения В, м).
- прогиб вала в точке приведения В, м).
Относительная приведенная масса вала:
консольного
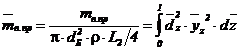 ; (37)
; (37)
однопролетного
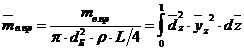 , (38)
, (38)
где  - приведенная масса вала, кг;
- приведенная масса вала, кг;
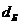 - диаметр вала на опоре Б, м.
- диаметр вала на опоре Б, м.
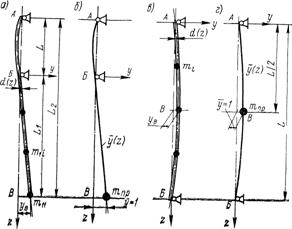
а, в - реальные валы со многими сосредоточенными массами 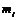 ; б, г - идеализированные расчетные схемы валов с одной приведенной массой
; б, г - идеализированные расчетные схемы валов с одной приведенной массой 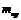 , сосредоточенной в точке приведения В
, сосредоточенной в точке приведения В
Рисунок 14 - К расчету консольного (а, б) и однопролетного (в, г) валов по методу приведения
Относительная приведенная масса i-го конструктивного элемента установленного на валу:
консольном
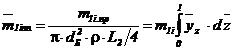 , (39)
, (39)
где т1i пр - приведенная масса элемента (диска, мешалки, барабана и т. п.) массой m1i, установленного на консоли вала, кг;
однопролетном
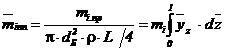 , (40)
, (40)
где тi пр - приведенная масса элемента, имеющего массу mi, кг.
Относительная приведенная масса вала и элемента, установленных на валу:
консольном
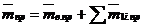 ; (41)
; (41)
однопролетном
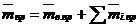 . (42)
. (42)
Относительная критическая скорость вала
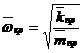 . (43)
. (43)
Переход от безразмерного значения критической скорости к ее размерному значению 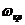 осуществляется для консольных и однопролетных валов сплошного поперечного сечения соответственно по формулам, вытекающим из выражений (35)—(43):
осуществляется для консольных и однопролетных валов сплошного поперечного сечения соответственно по формулам, вытекающим из выражений (35)—(43):
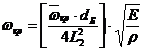 ;
; 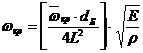 . (44)
. (44)
Таким образом, реальный вал сложной конструкции, нагруженный несколькими массами, в том числе и собственной массой, в рассматриваемом методе заменяется более простой идеализированной моделью вала (рисунок 14, б, г) с одной сосредоточенной приведенной массой 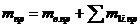 (консольный) или
(консольный) или 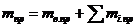 (однопролетный) и приведенными параметрами, вычисляемыми по формулам (35)—(43). За точку В приведения распределенных и сосредоточенных масс принято место крепления массы
(однопролетный) и приведенными параметрами, вычисляемыми по формулам (35)—(43). За точку В приведения распределенных и сосредоточенных масс принято место крепления массы 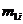 на консоли (рисунок 14, а) и середина пролета для однопролетного вала (см. рисунок 14, г), а форма оси
на консоли (рисунок 14, а) и середина пролета для однопролетного вала (см. рисунок 14, г), а форма оси 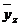 изогнутого вала считается совпадающей с формой оси при статическом изгибе вала поперечной силой, приложенной в точке приведения, и определяется следующими уравнениями:
изогнутого вала считается совпадающей с формой оси при статическом изгибе вала поперечной силой, приложенной в точке приведения, и определяется следующими уравнениями:
консоль БВ консольного ступенчатого вала
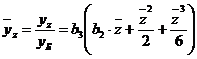 ; (45)
; (45)
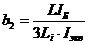 ;
; 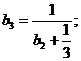 (46)
(46)
где 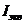 - эквивалентный момент инерции сечения вала в пролете АВ, определяемый по формулам (53) и (54);
- эквивалентный момент инерции сечения вала в пролете АВ, определяемый по формулам (53) и (54);
однопролетный вал постоянного поперечного сечения и пролет АБ консольного вала
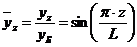 . (47)
. (47)
Как показывают расчеты, однопролетные валы нецелесообразно выполнять с переменным сечением по длине (конструктивные ступени вала, имеющие диаметр, отличающийся на ±10 % от диаметра рала dв в точке приведения В, в расчетах допустимо не учитывать).
Однако консольные валы целесообразно проектировать ступенчатыми, близкими по форме балке равного сопротивления изгибу (см. рисунок 15), что позволяет уменьшить массу ротора и несколько увеличить его  .
.
Диаметр вала dБ в опорном сечении Б рассчитывается по формуле
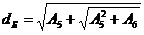 , (48)
, (48)
где для виброустойчивого вала: консольного при 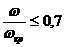 :
:
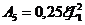 ;
; 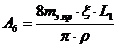 ;
; 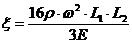 ;
;
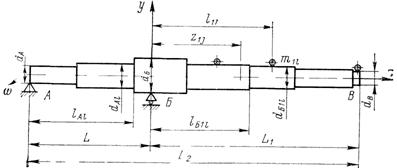
Рисунок 15 - Расчетная схема консольного ступенчатого вала с сосредоточенными массами т1i на консоли вала
консольного при 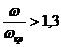 ;
;
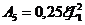 ;
; 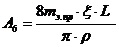 ;
; 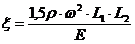 ;
;
однопролетного при 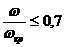 ;
;
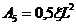 ;
; 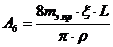 ;
; 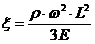 .
.
Приведенная масса элементов определяется по формулам:
для консольного вала
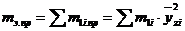 , (49)
, (49)
для однопролетного вала
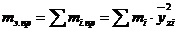 (50)
(50)
Формула (48), позволяющая быстро выполнить проектный расчет виброустойчивого вала, получена на основе условий (35)-(44).
После определения диаметра dБ по формуле (48) необходимо вычислить диаметры dA и dB из условий прочности при кручении, а диаметры ступеней dAl, dA2, dA3 в пролете вала принять из конструктивных соображений dAi 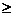 dA сучетом закрепления на валу тех или иных деталей. Диаметры ступеней на консоли необходимо принять в соответствии с формулой
dA сучетом закрепления на валу тех или иных деталей. Диаметры ступеней на консоли необходимо принять в соответствии с формулой
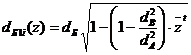 . (51)
. (51)
Условие (51) позволяет замкнуть систему уравнений (35)—(43) и получить расчетную формулу (44) для 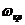 ступенчатого многомассового вала. При этом показатель степени t формулы (51) выбирается согласно рисунку 16 в зависимости от относительной приведенной массы элементов
ступенчатого многомассового вала. При этом показатель степени t формулы (51) выбирается согласно рисунку 16 в зависимости от относительной приведенной массы элементов 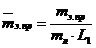 и относительной податливости пролета
и относительной податливости пролета
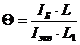 . (52)
. (52)
Эквивалентный момент инерции пролета с двумя ступенями dAl, dA2 (см. рисунок 15) рассчитывается по формуле
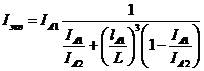 (53)
(53)
и с тремя ступенями dA1, dA2, dA3 - по формуле
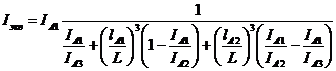 , (54)
, (54)
где 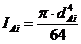 ;
; 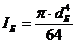 .
.
Тогда 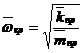 ,
,
где 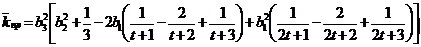
;(55)
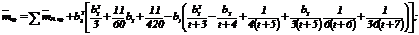 (56)
(56)
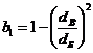 (57)
(57)
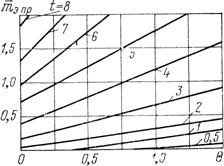
Рисунок 16 - Зависимость показателя степени t от параметров относительной приведенной массы 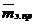 установленных элементов и относительной податливости пролета
установленных элементов и относительной податливости пролета 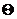 консольного ступенчатого вала
консольного ступенчатого вала
Изложенная выше методика касалась проектного расчета вала. При проверочном же расчете, когда значение dБ задано, необходимо определить 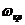 по формуле (44). При dB = dБ = const, т. е. b1 = 0 (консоль постоянного по длине поперечного сечения), что часто встречается на практике, формула для
по формуле (44). При dB = dБ = const, т. е. b1 = 0 (консоль постоянного по длине поперечного сечения), что часто встречается на практике, формула для 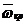 упрощается:
упрощается:
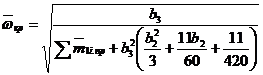 . (58)
. (58)
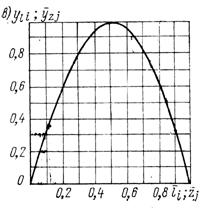
Зависимость (58) приведена на рисунке 17 в виде графика, способствующего ускорению расчетов валов на виброустойчивосгь.
Для консольных валов постоянного поперечного сечения расчет еще более упрощается, так как dБ = dB = dA = d; 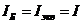 ;
; 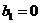 , и формулы (46) принимают вид
, и формулы (46) принимают вид
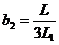 ;
; 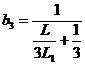 .
.
Это позволило уравнения (45) и (47) представить на рисунке 18 в виде графиков, способствующих также ускорению расчета валов.
Для однопролетного вала постоянного поперечного сечения 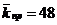 и
и 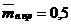 . Вычислив по формулам (41), (42), (49), (50)
. Вычислив по формулам (41), (42), (49), (50) 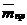 , легко получить далее по формуле (43)
, легко получить далее по формуле (43) 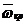 и найти по формуле (44) размерное значение критической скорости однопролетного вали заданного поперечного сечения.
и найти по формуле (44) размерное значение критической скорости однопролетного вали заданного поперечного сечения.
8.2 Расчет валов на жесткость
При расчете динамических прогибов вала необходимо учитывать: радиальные перемещения 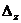 сечений из-за имеющихся зазоров сечений из-за имеющихся зазоров 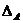 и и 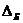 в подшипниках (таблицы 11, 12), начальную изогнутость в подшипниках (таблицы 11, 12), начальную изогнутость 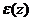 из-за погрешностей его изготовления (таблица 13) и эксцентриситеты e1 и e1i из-за погрешностей его изготовления (таблица 13) и эксцентриситеты e1 и e1i
| 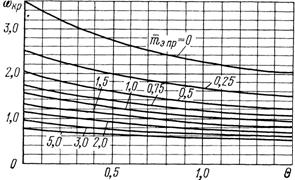 Рисунок 17 - Зависимость критической скорости
Рисунок 17 - Зависимость критической скорости 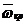 от параметров: относительной приведенной массы от параметров: относительной приведенной массы 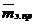 установленных элементов и относительной податливости пролета установленных элементов и относительной податливости пролета 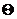 для вала, имеющего на консоли постоянное поперечное сечение и ступенчатое в пролете для вала, имеющего на консоли постоянное поперечное сечение и ступенчатое в пролете
|
сосредоточенных масс 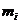 и
и 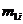 (рисунок 19).
(рисунок 19).
Таблица 11 - Радиальные зазоры (Ад и А б), мкм, по основному ряду в радиальных подшипниках
| Внутренний диаметр подшипников, мм | Подшипники качения | |||
| однорядный шариковый | однорядный роликовый * | двухрядный сферический роликовый ** | ||
| взаимозаменяемый | невзаимозаменяемый | |||
| 30—40 | 12—26 | 20—55 | 30—45 | 25-40 |
| 40—50 | 12—29 | 20—55 | 30—45 | 30-45 |
| 50—65 | 13—33 | 25—65 | 35—55 | 30—50 |
| 65—80 | 14—34 | 30—70 | 40—60 | 40—60 |
| 80—100 | 16—40 | 35-80 | 45—65 | 45—70 |
| 100—120 | 20—46 | 40—90 | 50—75 | 50—80 |
| 120—140 | 23—53 | 45—100 | 60—90 | 60—90 |
| 140—160 | 23—58 | 50—115 | 70—105 | 65-100 |
| 160—180 | 24—65 | 60—125 | 75—115 | 70—110 |
| 180—200 | 29—75 | 65—135 | 80—120 | 80—120 |
| 200—225 | 33—83 | 75—150 | 90—135 | 90-140 |
| 225—250 | 35—90 | 90—165 | 100- 150 | 100—150 |
| 250—280 | 40—100 | 100—180 | 110—165 | 110—170 |
| 280—315 | 45—105 | 110—195 | 120—180 | 120—180 |
| 315—355 | 50—115 | 125—215 | 135—205 | 140—210 |
| 355—400 | 55—125 | 140—235 | 150—225 | 150—230 |
| 400—450 | — | 160—260 | 165—245 | 170—260 |
| 450—500 | — | 180—290 | 185—275 | 190—290 |
| * Короткие цилиндрические ролики и цилиндрическое отверстие. ** Цилиндрическое отверстие. |
На основании развития метода привидения получены важные соотношения:
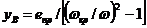 ; (59)
; (59)
Таблица 12 - Радиальные зазоры в подшипнике скольжения
| Таблица 13 - Начальная изогнутость ε (z) вала
| ||||||||||||
| 
| ||||||||||||
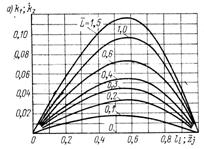
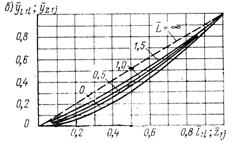
| Рисунок 18 - Графики для определения безразмерных прогибов
а - в пролете консольного вала  ; ; 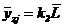 , где , где 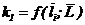 ; ; 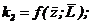 б - на консоли консольного вала б - на консоли консольного вала 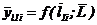 ; ; 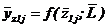 ; в - однопролетного вала ; в - однопролетного вала 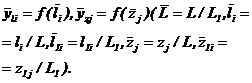
|
для пролета АБ консольного и однопролетного валов:
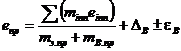 ; (60)
; (60)
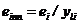 ; (61)
; (61)
для консоли БВ консольного вала:
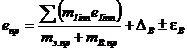 ; (62)
; (62)
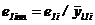 , (63)
, (63)
где епр, еiпр и е1iпр - приведенные эксцентриситеты соответственно системы и сосредоточенных масс mi и m1i. Знак плюс в формуле (61) принимается для докритической, а минус - для закритической областей работы вала. Начальная изогнутость вала в точке приведения εВ задается из соображений технологии изготовления вала. Параметр εВ связан с изогнутостью (таблица 14) в любом сечении вала соотношением
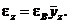 (64)
(64)
Смещение ΔВ вала в точке приведения связано с зазорами в подшипниках соотношениями:
консольный вал
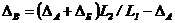 ; (65)
; (65)
однопролетный вал
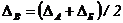 . (66)
. (66)
Формулы (64) и (65) вытекают из следующих более общих зависимостей: для пролета АБ консольного вала
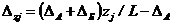 ; (67)
; (67)
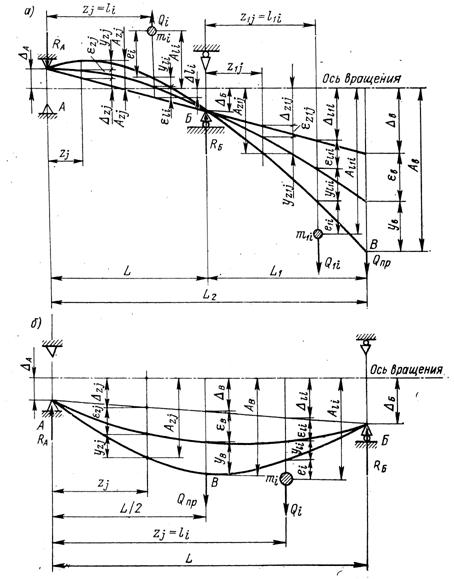
|
| Рисунок 19 - Смещение оси вала и центров сосредоточенных на нем масс а - консольного вала; б - однопролетного вала |
консольного участка БВ
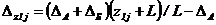 ; (68)
; (68)
однопролетного вала
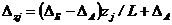 ; (69)
; (69)
Если принять, что начальные смещения вала равны нулю, а единственная масса mi=m1i=m закреплена на идеализированном (без учета массы вала) валу с эксцентриситетом ei=e1i=e, т.е., если mпр=m; εВ=ΔВ=0, тогда епр=е и формула (59) упрощается до уже известного выражения (12)
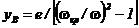 ,
,
которое, следовательно, является частным случаем более общего условия (59), наглядно характеризующего влияние на динамический прогиб ряда важных параметров. Определив прогиб уВ и учитывая форму оси изогнутого вала по формулам (46), (48), можно найти прогибы уz, и перемещения Аz других точек вала (см. рисунок 19):
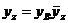 ; (70)
; (70)
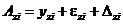 ;
; 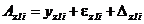 ; (71)
; (71)
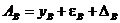 , (72)
, (72)
а также найти динамические смещения центров масс:
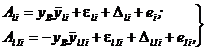 (73)
(73)
где 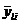 ,
, 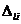 , εli,
, εli, 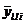 ,
, 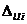 вычисляются по формулам (64) - (70) при z=li и z=l1i. Соотношения (71) позволяют перейти к проверке условий жесткости:
вычисляются по формулам (64) - (70) при z=li и z=l1i. Соотношения (71) позволяют перейти к проверке условий жесткости:
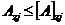 ;
; 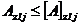 , (74)
, (74)
где 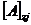 и
и 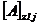 - допускаемые перемещения вала соответственно в пролете и на консоли.
- допускаемые перемещения вала соответственно в пролете и на консоли.
В ряде случаев валы подвергаются воздействию постояннодействующей поперечной к оси вала силы Q (силы тяжести горизонтальных роторов, несбалансированные гидродинамические поперечные силы вертикальных валов мешалок и т.п.). И в этом случае метод приведения позволяет достаточно точно учесть ее влияние на прогибы и перемещения вала.
Для пролета АБ валов (см. рисунок 19), нагруженных поперечными силами Q1, приведенная поперечная сила вычисляется по формуле
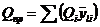 , (75)
, (75)
а для консоли БВ вала (см. рисунок 19, а) - по формуле
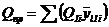 . (76)
. (76)
Тогда динамический прогиб в точке приведения В
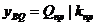 . (77)
. (77)
Это позволяет получить максимальные значения динамических перемещений сечений вала АzjQ, Az1jQ и центров масс деталей АljQ, Al1jQ с учетом силы Q:
в пролете АБ однопролетного и консольного валов:
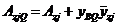 ; (78)
; (78)
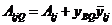 ;
;
на консоли БВ консольного вала:
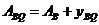 ; (79)
; (79)
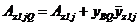 ;
; 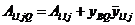 .
.
Полученные соотношения (70) - (79) позволяют перейти к проверке условий жесткости ротора, если заданы допускаемые перемещения рассматриваемой конструкции ротора:
для пролета АБ
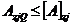 ; (80)
; (80)
для консоли БВ
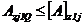 . (81)
. (81)
Например, для уплотнения валов аппаратов с мешалками значения 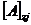 и
и 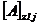 приведены в таблице14.
приведены в таблице14.
Таблица 14 - Допускаемые динамические перемещения вала (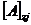 и
и 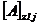 , мм) в месте установки уплотнения
, мм) в месте установки уплотнения
| Частота вращения вала перемешивающего устройства, об/мин | Уплотнение | |||
| торцовое | сальниковое | манжетное | гидравлический затвор | |
| До 100 100-500 500-750 750-2900 | 0,25 0,25 0,15 0,10 | 0,10 - - - | 0,15 0,15 0,10 - | 0,25 0,25 0,25 - |
Прочность. Для составления условий прочности вначале необходимо вычислить сосредоточенные силы (см. рисунок 19):
в пролете АБ
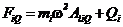 ; (82)
; (82)
на консоли БВ
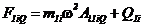 , (83)
, (83)
и приведенную центробежную силу собственной массы вала в точке приведения
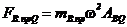 .
.
| Далее вал рассматривается как обычная двухопорная статически определимая балка, нагруженная сосредоточенными поперечными силами. Для этого строятся эпюры изгибающих и крутящих моментов, выясняются координаты опасных | 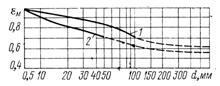 1 - углеродистая сталь; 2 - легированная сталь
Рисунок 20 - Зависимость масштабного фактора εМ от диаметра d и материала вала
1 - углеродистая сталь; 2 - легированная сталь
Рисунок 20 - Зависимость масштабного фактора εМ от диаметра d и материала вала
|
сечений вала и проводится расчет на усталостную или статическую прочность по следующему условию:
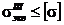 , (84)
, (84)
где 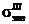 - эквивалентное напряжение по третьей теории прочности. При нагружении вала поперечными силами Qi значение допускаемого напряжения [σ] необходимо рассчитывать по формуле
- эквивалентное напряжение по третьей теории прочности. При нагружении вала поперечными силами Qi значение допускаемого напряжения [σ] необходимо рассчитывать по формуле
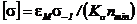 , (85)
, (85)
где Кσ - эффективный коэффициент концентрации напряжений (см. таблицу 14); nmin - минимальный запас прочности вала; εM - масштабный фактор (коэффициент влияния абсолютных размеров вала, см. рисунок 20); σ-1 - предел выносливости материала вала, 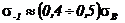 .
.
Если же к валу не приложены постоянно действующие поперечные силы Qi, то величину [σ] можно рассчитать по формуле
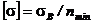 , (86)
, (86)
где σВ - предел прочности материала вала (таблица 16).
Таблица 15 - Эффективный коэффициент Кσ концентрации напряжений
| Предел прочности материала σВ, МПа | 
| 
| 
| |||||||||||
| Кσ | ||||||||||||||
| для валов со шпоночной канавкой, выполненной фрезой | для валов с метрической резьбой | |||||||||||||
| торцовой | дисковой | |||||||||||||
| 1,30 1,38 1,46 1,54 1,62 1,69 1,77 1,92 | 1,51 1,64 1,76 1,89 2,01 2,14 2,26 2,50 | 1,45 1,78 1,96 2,20 2,32 2,47 2,61 2,90 | ||||||||||||
| Предел прочности материала σВ, МПа | 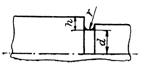
| |||||||||||||
| Кσ | ||||||||||||||
| для валов с выточкой при h/r | ||||||||||||||
| 0,5 | 0,1 | |||||||||||||
| при r/d | ||||||||||||||
| 0,01 | 0,02 | 0,03 | 0,05 | 0,10 | 0,01 | 0,02 | ||||||||
| 1,88 1,93 1,98 2,04 2,09 2,15 2,20 2,31 | 1,79 1,84 1,82 1,95 2,00 2,06 2,11 2,22 | 1,72 1,77 1,82 1,87 1,92 1,97 2,02 2,12 | 1,61 1,66 1,71 1,77 1,82 1,88 1,93 2,04 | 1,44 1,48 1,52 1,55 1,59 1,62 1,66 1,73 | 2,09 2,15 2,21 2,27 2,37 2,39 2,45 2,57 | 1,99 2,05 2,11 2,17 2,20 2,28 2,35 2,49 | ||||||||
| Предел прочности материала σВ, МПа | Кσ | |||||||||||||
| для валов с выточкой при h/r | ||||||||||||||
| при r/d | ||||||||||||||
| 0,03 | 0,05 | 0,01 | 0,02 | 0,03 | 0,01 | 0,02 | ||||||||
| 1,91 1,97 2,03 2,08 | 1,79 1,85 1,91 1,97 | 2,29 2,36 2,43 2,50 | 2,18 2,25 2,32 2,38 | 2,10 2,16 2,22 2,28 | 2,38 2,47 2,56 2,64 | 2,28 2,35 2,42 2,49 | ||||||||
Продолжение таблицы 15
| 2,14 2,19 2,25 2,36 | 2,03 2,09 2,15 2,27 | 2,56 2,63 2,70 2,84 | 2,45 2,51 2,58 2,71 | 2,35 2,41 2,47 2,59 | 2,73 2,81 2,90 3,07 | 2,56 2,63 2,70 2,84 |
Таблица 16 - Предел прочности материала валов при поставке
| Марка стали | σВ, МПа | Марка стали | σВ, МПа |
| Ст5 20Х 40Х 40ХН 12ХН3А | 12Х2Н4А 18ХГТ 15ХМ 12Х18Н10Т 30ХГТ 25Х2ГТН |
Приложение 1
Таблица 1.1 - Плотность твердых материалов [7]
| Материал | Плотность, кг/м3 | Материал | Плотность, кг/м3 |
| Алебастр Антрацит Апатит Асбест Бетон Винипласт Гипс кристаллический Глина сухая Гранит Зола Земля сухая Известняк Каолин Каучук Кварц Керамика кислотоупорная Кирпич обыкновенный Кокс Колчедан серый Кожа сухая Литьё каменное Мел кусковой Мрамор Парафин Паронит | - | Песок сухой Поташ Пробка Резина Селитра натриевая Сода кристаллическая Соль каменная Сосна Стекло Текстолит Уголь древесный Уголь каменный Фаолит Цемент Эмаль Металлы Сталь чугун серый Медь катанная Латунь Алюминий Свинец |
Таблица 1.2 - Плотность жидких веществ и водных растворов в зависимости от температуры [7]
| Вещество | Плотность, кг/м3 | |||||
| 0 С° | 20 С° | 40 С° | 60 С° | 80 С° | 100 С° | |
| Азотная кислота, 100% » » 50% Аммиак жидкий Аммиачная вода, 25% Анилин Ацетон Бензол Бутиловый спирт Вода Гексан Глицерин, 50% Диоксид серы (жидк.) Дихлорэтан Диэтиловый эфир Изопропиловый спирт Кальций хлористый, 25% раствор | ||||||
Продолжение таблицы 1.2
| μ-Ксилол Метиловый спирт, 100% » » 40% Муравьиная кислота Натр едкий, 50% раствор » » 40% » » » 30% » » » 20% » » » 10% » Натрий хлористый, 20% раствор Нитробензол Октан Олеум, 20% Пропиловый спирт Серная кислота, 98% » » 92% » » 75% » » 60% Сероуглерод Соляная кислота, 30% Толуол Уксусная кислота, 100% » » 50% Фенол (расплавленный) Хлорбензол Хлороформ Четыреххлористый углерод Этилацетат Этиловый спирт, 100% » » 80% » » 60% » » 40% » » 20% | ― |
Таблица 1.3 - Динамические коэффициенты вязкости воды [7]
| Температура, С° | Динамический коэффициент вязкости, мПа·с (сП) | Температура, С° | Динамический коэффициент вязкости, мПа·с (сП) | Температура, С° | Динамический коэффициент вязкости, мПа·с (сП) |
| 1,792 1,731 1,73 1,619 1,567 1,519 1,473 1,428 | 0,7523 0,7371 0,7225 0,7085 0,6947 0,6814 0,6685 0,6560 | 0,4233 0,4174 0,4117 0,4061 0,4006 0,3952 0,3900 0,3849 | |||
Продолжение таблицы 1.3
| 20,2 | 1,386 1,846 1,308 1,271 1,236 1,203 1,171 1,140 1,111 1,083 1,056 1,030 1,005 1,000 0,9810 0,9579 0,9358 0,9142 0,8937 0,8737 0,8545 0,8360 0,8180 0,8007 0,7840 0,7679 | 0,6439 0,6321 0,6207 0,6097 0,5988 0,5883 0,5782 0,5683 0,5588 0,5494 0,5404 0,5315 0,5229 0,5146 0,5064 0,4985 0,4907 0,4832 0,4759 0,4688 0,4618 0,4550 0,4483 0,4418 0,4355 0,4293 | 0,3799 0,3750 0,3702 0,3655 0,3610 0,3565 0,3521 0,3478 0,3436 0,3395 0,3355 0,3315 0,3276 0,3239 0,3202 0,3165 0,3130 0,3095 0,3060 0,3027 0,2994 0,2962 0,2930 0,2899 0,2868 0,2838 | |||||||
Приложение 2
Пример 1
На центрифуге типа ФГН-180 проводится разделение водного раствора гипса в количестве 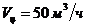 . Массовое соотношение твердой и жидкой фаз в исходной суспензии Т:Ж=1:3. Влажность образующегося осадка не должна превышать 20% масс (
. Массовое соотношение твердой и жидкой фаз в исходной суспензии Т:Ж=1:3. Влажность образующегося осадка не должна превышать 20% масс (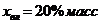 ). Экспериментально установлено, что продолжительность центрифугирования
). Экспериментально установлено, что продолжительность центрифугирования 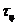 =2 мин; выгрузки (среза) осадка
=2 мин; выгрузки (среза) осадка 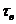 =1 мин; объем фильтрата, полученного за один цикл,
=1 мин; объем фильтрата, полученного за один цикл, 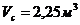 . Определить коэффициент заполнения ротора осадком и количество центрифуг. Плотность фильтрата пронять равной 1000 кг/м3 (
. Определить коэффициент заполнения ротора осадком и количество центрифуг. Плотность фильтрата пронять равной 1000 кг/м3 (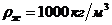 ).
).
1 Техническая характеристика центрифуги ФГН-180 (см. таблицу 8)
внутренний диаметр ротора D=1800 мм
частота вращения n=720 об/мин
фактор разделения Ф=520
рабочий объем ротора Vр=0,85м3
2 Продолжительность питания для достижения максимальной средней производительности
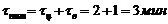 .
.
3 Продолжительность полного цикла центрифугирования
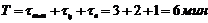 .
.
4 производительность центрифуги по фильтрату
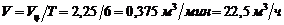 .
.
5 Масса осадка, полученного за один цикл:
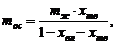 кг,
кг,
здесь 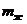 - масса фильтрата, полученного за один цикл.
- масса фильтрата, полученного за один цикл.
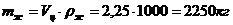 ,
,
где 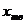 - концентрация твердой фазы в суспензии (массовые доли).
- концентрация твердой фазы в суспензии (массовые доли).
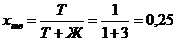 ;
;
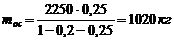 .
.
6 Объем осадка, полученного за один цикл:
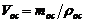 , м3,
, м3,
где 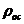 - плотность влажного осадка
- плотность влажного осадка
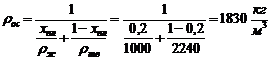 ,
,
где 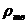 = 2240
= 2240 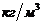 - плотность гипса (таблица 1, приложение 1)
- плотность гипса (таблица 1, приложение 1)
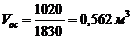 .
.
7 Коэффициент заполнения барабана центрифуги осадком составит
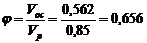 .
.
8 Средняя производительность центрифуги по суспензии
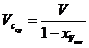 ,
,
где 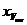 - концентрация твердой фазы в суспензии (объемные доли).
- концентрация твердой фазы в суспензии (объемные доли).
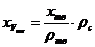 ,
,
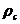 - плотность суспензии, кг/м3:
- плотность суспензии, кг/м3:
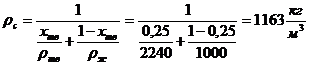 ;
;
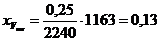 ;
;
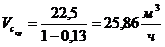 .
.
9 Количество центрифуг
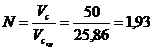 .
.
Принимаем две центрифуги.
Пример 2
Отстойная центрифуга типа ОГН-1800 должна работать на водной суспензии мела. Определить производительность центрифуги по питанию. Температура суспензии 40°С. Размер наименьших частиц мела d = 2 мкм. Цикл работы центрифуги составляет 20 мин; из них 18 мин - подача суспензии, 2 мин - разгрузка осадка
Техническая характеристика центрифуги ОГН-1800(см. таблицу 8)
внутренний диаметр ротора Dвн=1800 мм
длина ротора L=700 мм
внутренний диаметр кольцевого слоя (диаметр борта) D0=1300 мм
частота вращения n=720 об/мин
Производительность определяем по уравнению (7)
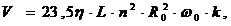 м3/ч.
м3/ч.
Скорость осаждения частиц находим по выражению Стокса
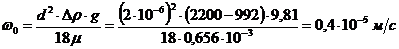 .
.
Плотность мела 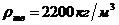 (таблица 1, приложение 1), воды при 40°
(таблица 1, приложение 1), воды при 40° 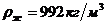 (таблица 2, приложение 1), коэффициент динамической вязкости воды при 40°
(таблица 2, приложение 1), коэффициент динамической вязкости воды при 40° 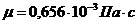 (таблица 3, приложение 1).
(таблица 3, приложение 1).
Скорость осаждения под действием центробежной силы
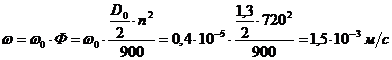
Проверяем режим осаждения
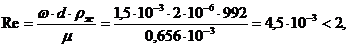
т.е. режим ламинарный.
Находим
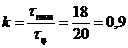 .
.
Принимаем 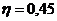 .
.
Тогда производительность центрифуги
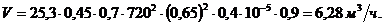
Пример 3
Выбрать центрифугу для разделения суспензии по следующим данным: требуемая производительность по суспензии 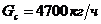 ; по сухому осадку
; по сухому осадку 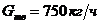 ; массовая концентрация твердой фазы в суспензии
; массовая концентрация твердой фазы в суспензии 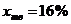 ; плотность твердой фазы -
; плотность твердой фазы - 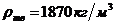 , жидкой
, жидкой 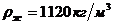 . Целевой продукт - твердая фаза, размеры частиц ее лежат в пределах 10…100 мкм. Осадок рыхлый, требуется промывка его в центрифуге; измельчение осадка допустимо. Влажность осадка не должна превышать 20% (
. Целевой продукт - твердая фаза, размеры частиц ее лежат в пределах 10…100 мкм. Осадок рыхлый, требуется промывка его в центрифуге; измельчение осадка допустимо. Влажность осадка не должна превышать 20% (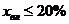 массовых)
массовых)
Принять время полного цикла обработки суспензии 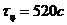 .
.
1 Предварительный выбор центрифуги проводится на основе анализа свойств суспензии, указанных в исходных данных, и технических требований. Для этого необходимо рассчитать объемную концентрацию твердой фазы и объемную производительность центрифуги по суспензии.
Плотность суспензии
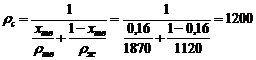 кг/м3.
кг/м3.
Объемная концентрация суспензии
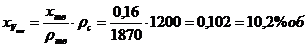 .
.
Объемная производительность по суспензии
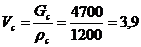 м3/ч.
м3/ч.
Необходимость хорошей промывки осадка и низкая его влажность указывает на возможность применения