ТЮМЕНСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЕГАЗОВЫЙ УНИВЕРСИТЕТ
ИНСТИТУТ НЕФТИ И ГАЗА
Кафедра Кибернетических систем
Методические указания
к лабораторной работе № 4
по дисциплине «Теория автоматического управления»
на тему «Синтез линейных систем»
Тюмень 2008
1 Цель работы: для заданной динамической системы управления с помощью частотного метода ЛАЧХ определить непрерывное корректирующее устройство, добавление которого в систему позволяет получить необходимые показатели качества процесса управления.
Теоретические сведения
При синтезе систем автоматического управления (САУ) могут быть выделены следующие частные задачи:
- обеспечение устойчивости;
- повышение запаса устойчивости;
- повышение точности регулирования в типовых режимах;
- улучшение качества переходных процессов.
Если при решении задачи повышения запаса устойчивости и качества САУ невозможно добиться положительных результатов простым изменением параметров системы (коэффициентов передачи отдельных звеньев, постоянных времени и т.п.), в таком случае возникает необходимость введения в САУ дополнительных устройств. Обеспечение устойчивости и качественной работы САУ с помощью дополнительных устройств называется коррекцией, а сами устройства – корректирующими.
Благодаря своей простоте метод логарифмических частотных характеристик оказывается наиболее простым методом синтеза стационарных линейных систем. Так как для минимально-фазовых систем существует однозначная зависимость между ЛАЧХ и ЛФЧХ, при синтезе системы достаточно построить желаемую ЛАЧХ.
В инженерной практике синтез корректирующих устройств с помощью логарифмических частотных характеристик осуществляется в следующем порядке:
1) по виду передаточной функции WН (р) строится ЛАХ исходной разомкнутой нескорректированной САУ 
;
2) с учетом всей совокупности требований, предъявляемых к качеству процесса регулирования САУ, строится желаемая логарифмическая амплитудная частотная характеристика 
разомкнутой системы;
3) на основании сравнения ЛАХ нескорректированной системы с желаемой определяется ЛАХ корректирующего звена 
. Так как у минимально-фазовых систем ЛАХ однозначно определяет весь характер переходного процесса, то для осуществления синтеза достаточно рассмотрения одних ЛАХ;
4) по виду определяются передаточная функция корректирующего звена WКЗ (р), ее параметры и техническая реализация;
5) производится проверочный расчет переходного процесса с учетом реальной структуры и места включения корректирующего звена, оценка запасов устойчивости и показателей качества скорректированной САУ.
Если скорректированная САУ удовлетворяет заданным показателям качества, то синтез на этом заканчивается. В противном случае уточняется структура и параметры корректирующего звена; далее снова производится проверочный расчет.
Схемы включения корректирующих звеньев
Корректирующие звенья включаются в структурную схему системы последовательно либо в цепь обратной связи (параллельно).
2.1.1 Последовательная коррекция это коррекция САУ с помощью корректирующего устройства, последовательно включенного в прямую цепь системы (непосредственно в контур регулирования).
Рисунок 1 – последовательная коррекция
Wнск (s) – передаточная функция нескорректированной системы;
Wк (s) – передаточная функция корректирующего звена;
Wск (s) – передаточная функция скорректированной системы.
Суть методики синтеза заключается в определении Wск (s), обеспечивающей заданные показатели качества управления и в расчете по ней Wк (s).
Wск (s) = Wк (s) · Wнск (s),
Wск (jω) = Wк (jω) · Wнск (jω),
|Wск (jω)| = |Wк (jω)| · |Wнск (jω)|,
Lск (ω) = Lк (ω) + Lнск (ω),
Lк (ω) = Lск (ω) - Lнск (ω).
По полученному графику Lк (ω) восстанавливают соответствующую передаточную функцию (ПФ) корректирующего устройства Wк (s).
Корректирующие звенья последовательного типа могут составляться из различной по своей физической природе элементов – электрических, механических, гидравлических и т.д. Наиболее просто такие звенья могут быть составлены из электрических R-, C- и L-элементов. Последовательное корректирующее устройство часто включают или непосредственно после датчика рассогласования, или после предварительного усилителя.
Последовательные корректирующие звенья.
- пассивные интегрирующие звенья, подавляют усиление на высоких частотах (ВЧ) и вносят в некотором интервале частот отрицательный фазовый сдвиг;
- пассивные дифференцирующие звенья, подавляют низкие частоты (НЧ) и вносят положительный фазовый сдвиг;
- интегро-дифференцирующие звенья, подавляют усиление в некотором интервале средних частот (СЧ), вносимый фазовый сдвиг вначале отрицателен, затем нулевой, а при дальнейшем росте становится положительным.
2.1.2 Параллельная коррекция это коррекция САУ с помощью корректирующего устройства, включенного в цепь специальной обратной связи. Обратные связи имеют наиболее широкое применение вследствие простоты технической реализации. К тому же, корректирующие устройства различного типа оказывают различное влияние на содержащиеся в системе нелинейности. Отрицательные же обратные связи имеют свойство уменьшать влияние нелинейностей тех участков цепи регулирования, которые ими охватываются.
Рисунок 2 – параллельная коррекция
Wнск (s) = W1 (s) · Wохв (s) · W2 (s),
,
,
.
1 рассмотрим диапазон частот, где 
<< 1, это область низких частот. 
, 
.
2 рассмотрим диапазон частот, где >> 1. В этом случае 
,
,
.
Таким образом, для нахождения ЛАЧХ корректирующего звена необходимо построить 5 графиков:
1. Lнск (ω);
2. Lск (ω);
3. Lп (ω) = Lнск (ω) - Lск (ω);
4. Lохв (ω);
5. Lос (ω) = Lп (ω) - Lохв (ω).
В качестве корректирующего звена при параллельной коррекции обычно используется дифференцирующее звено с замедлением: 
, 
может быть больше и меньше 1.
Выбор желаемой ЛАЧХ
Построение желаемой ЛАХ удобно первоначально осуществлять раздельно в низкочастотном (I), среднечастотном (II) и высокочастотном (III) диапазонах.
2.2.1 Построение ЛАХ в низкочастотном диапазоне
На низкочастотном участке, где вид 
определяется в основном требованиями к точности регулирования, а следовательно, величиной коэффициента усиления системы, порядком ее астатизма, значением коэффициента ошибки и т.д.
Если в системе, отрабатывающей ступенчатый входной сигнал 
, допустимая статическая ошибка не должна превышать значения 
, то величина коэффициента усиления разомкнутой скорректированной системы:
.
При этом на участке низких частот желаемая ЛАХ проводится параллельно оси абсцисс с ординатой 
. В случае, когда статическая ошибка недопустима ( = 0), то скорректированная система должна быть астатической.
Если в астатической системе с астатизмом первого порядка требуется обеспечить слежение за сигналом 
, то ее коэффициент усиления определяется величиной максимально допустимой ошибки по скорости 
:
.
При этом уравнение низкочастотного участка желаемой ЛАХ:
.
При синтезе следящих систем, входной сигнал которых заранее неизвестная функция времени, обычно указываются только максимально возможные значения скорости 
и ускорения 
входного сигнала и задаются требованием к величине максимально допустимой динамической ошибке регулирования . В этом случае подбирается эквивалентное гармоническое воздействие 
, амплитуда a и частота 
которого определяется значениями и :
, и 
. (2.1)
При воспроизведении линейной следящей системой эквивалентного гармонического воздействия ошибка регулирования также будет гармонической с той же частотой. Следовательно:
Полагая 
, имеем
,
откуда с учетом выражения (2.1):
,
или, логарифмируя последнее выражение получаем окончательно
. (2.2)
Из выражения (2.2) следует, что эквивалентное входное воздействие будет воспроизводиться следящей системой с ошибкой, не превышающей , если при 
ордината желаемой ЛАХ будет не менее
.
Точку К с координатами (
; 
) называют контрольной точкой (рис. 3).
На этом рисунке указаны две прямые, пересекающиеся в точке К, имеющие наклон -20 дБ/дек при 
и -40 дБ/дек при 
. Уравнения этих прямых получены на основании выражения (2.2) при уменьшении скорости и ускорения входного сигнала по отношению к их максимально возможным значениям. Данные прямые представляют собой границы запретной зоны для желаемой ЛАХ следящей системы с астатизмом первого порядка.
2.2.2 Построение ЛАХ в среднечастотном диапазоне
На среднечастотном участке желаемая ЛАХ в наибольшей степени зависит от требования к динамическим показателям качества регулирования, например, частотному показателю колебательности, времени регулирования и перерегулированию. На этом участке находится частота среза 
и определяется запас устойчивости по фазе.
Если качество регулирования системы оценивается по величине перерегулирования 
и времени регулирования 
, то, задавшись максимально допустимыми значения указанных показателей и , следует воспользоваться номограммой (рис. 4). По заданной величине перерегулирования (например, = 30 %), определяется величина :
,
где – частота среза желаемой ЛАХ. (Значению = 30 % на номограмме соответствует Pмакс = 1,28.) Поскольку допустимое значение задано, то можно вычислить необходимую частоту среза:
.
Рисунок 4 Номограмма для определения частоты среза желаемой ЛАХ
Вид желаемой ЛАХ в среднечастотном диапазоне должен гарантировать необходимый запас устойчивости системы по фазе, что в максимальной степени обеспечивается, когда 
в районе частоты среза имеет достаточно протяженный участок с наклоном -20 дБ/дек. Типы четырех возможных ЛАХ, удовлетворяющих этому условию, приведены в таблице 1. ЛАХ типа А и С соответствуют статическим системам, а ЛАХ типа B и D - астатическим системам с астатизмом первого порядка.
Таблица 1. Типовые ЛАХ.
| Тип ЛАХ | Наклоны асимптот, дБ/дек | |||
| Низкочастотный участок | Сопряженный участок | Среднечастотный участок | Высокочастотный участок | |
| А | - 40 | - 20 | - 40 | |
| B | - 20 | - 40 | - 20 | - 40 |
| C | - 40 | - 20 | - 60 | |
| D | - 20 | - 40 | - 20 | - 60 |
Для ЛАХ (рис. 5) примем следующие обозначения: 
– протяженность среднечастотного участка ; 
– протяженность участка желаемой ЛАХ, по которому сопрягаются низкочастотный и среднечастотный участки .
Имеется несколько рекомендаций по выбору частот 
и 
. Например, выбирают 
и 
. Наиболее простой является рекомендация, согласно которой интервалы частот (
– 
) и (
– 
) принимают равными 0,5…0,9 декады.
Еще один подход к выбору протяженности среднечастотного участка накладывает ограничение на абсолютную величину 
и 
, которые должны быть не ниже значений, определенных по специальной номограмме (рис. 6), обычно эти значения находятся в пределах от 12 до 16 дБ.
Для заданного Pмакс по номограмме находятся необходимые значения запасов устойчивости по модулю h + и по фазе 
. При этом вначале вычисляется Pмин по формуле
Pмин = 1 – Pмакс.
Проводятся горизонтальные касательные к кривым с индексами Pмакс и Pмин, по которым определяются значения h + и h - в дБ. На рис. 6 для значений Pмакс = 1,28 и Pмин = 0,28 найдены значения h + = 14 дБ и
h - = - 14 дБ. Вертикальная касательная к кривым определяет необходимый запас устойчивости по фазе
= 400.
Значения h + и h - определяют протяженность среднечастотного участка желаемой ЛАХ
= h +, 
= h -.
На указанном интервале частот фазо-частотная характеристика скорректированной системы не должна заходить в запретную область
.
Рисунок 6 Номограмма для определения запасов устойчивости по модулю h + и по фазе 
.
Если качество регулирования системы оценивается по величине частотного показателя колебательности M, то для определения протяженности участков l и l 1 можно воспользоваться данными, приведенными в таблице 2.
Таблица 2. Зависимость колебательности M от значений l и l 1.
| M | l | l 1 | |||
| ЛАХ типа А | ЛАХ типа B | ЛАХ типа C | ЛАХ типа D | ||
| 1,1 | 21,00 | 5,5 | 2,05 | 5,5 | 1,9 |
| 1,3 | 7,70 | 8,9 | 3,85 | 8,9 | 2,8 |
| 1,5 | 7,00 | 12,75 | 4,8 | 12,5 | 3,6 |
| 2,0 | 3,00 | 28,0 | 10,0 | 26,6 | 6,1 |
| 2,.5 | 2,33 | 42,0 | 14,1 | 40,0 | 7,2 |
Выбор граничных частот среднечастотного участка согласно приведенным рекомендациям дает несколько различные результаты. При окончательном их выборе следует исходить из того, что чем шире интервал частот (
; 
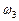), тем лучше будет переходный процесс. Однако практическая реализация желаемой ЛАХ при этом усложняется и, кроме того, излишняя протяженность среднечастотного участка снижает динамичность системы.
2.2.3 Построение ЛАХ в высокочастотном диапазоне
Вид желаемой ЛАХ в высокочастотном диапазоне определяет, например, такой показатель, как помехоустойчивость системы, но на качество регулирования поведение 
в этой частотной области влияет в незначительной степени. Поэтому на участке высоких частот с целью упрощения корректирующего звена допустимо совпадение наклонов асимптот желаемой ЛАХ и ЛАХ исходной нескорректированной системы.