В лотерее 1000 билетов. На один билет выпадает выигрыш 5000 рублей, на десять билетов – выигрыши по 1000 рублей, на пятьдесят билетов – выигрыши по 200 рублей, на сто билетов – выигрыши по 50 рублей; остальные билеты проигрышные. Покупается один билет. Тогда вероятность выигрыша равна 0,161
В урне находятся 1 белый и 2 черных шара. Из урны поочередно вынимают два шара, но после первого вынимания шар возвращается в урну, и шары в урне перемешиваются. Тогда вероятность того, что оба шара белые, равна 1/9
В лотерее 1000 билетов. На один билет выпадает выигрыш 5000 рублей, на десять билетов – выигрыши по 1000 рублей, на пятьдесят билетов – выигрыши по 200 рублей, на сто билетов – выигрыши по 50 рублей; остальные билеты проигрышные. Покупается один билет. Тогда вероятность выигрыша не менее 200 рублей равна 0,061
В урне лежит 2 белых и 4 черных шара. Последовательно, без возвращения и наудачу извлекают 3 шара. Тогда вероятность того, что все они будут черными, равна 1/5
В урне находятся 2 белых и 3 черных шара. Из урны поочередно вынимают два шара, но после первого вынимания шар возвращается в урну, и шары в урне перемешиваются. Тогда вероятность того, что оба шара черные, равна 9/25
В урне находятся 2 белых и 3 черных шара. Из урны поочередно вынимают два шара, но после первого вынимания шар возвращается в урну, и шары в урне перемешиваются. Тогда вероятность того, что оба шара белые, равна … 
В первом ящике 13 черных и 7 белых шаров, во втором – 8 черных и 7 белых. Из произвольного ящика достают один шар. Вероятность того, что он белый, равна 1/2*(7/20+7/15)
В первом ящике 7 красных и 9 синих шаров, во втором – 4 красных и 11 синих. Из произвольного ящика достают один шар. Вероятность того, что он красный, равна 1/2*(7/16+4/15)
В первом ящике 7 красных и 11 синих шаров, во втором – 5 красных и 9 синих. Из произвольного ящика достают один шар. Вероятность того, что он красный, равна 1/2*(7/18+5/14)
В первой урне 3 белых и 7 черных шаров. Во второй урне 5 белых и 5 черных шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар окажется белым, равна 0,4
В первом ящике 11 черных и 9 белых шаров, во втором – 8 черных и 7 белых. Из произвольного ящика достают один шар. Вероятность того, что он белый, равна 1/2*(9/20+7/15)
В первой урне 1 черный и 9 белых шаров. Во второй урне 4 белых и 6 черных шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар окажется белым, равна 0,65
В первой урне 2 белых и 8 черных шаров. Во второй урне 5 белых и 5 черных шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар окажется белым, равна 0,35
В первом ящике 12 черных и 5 белых шаров, во втором – 10 черных и 7 белых. Из произвольного ящика достают один шар. Вероятность того, что он белый, равна 1/2*(5/17+7/17)
В первом ящике 14 красных и 11 синих шаров, во втором – 5 красных и 12 синих. Из произвольного ящика достают один шар. Вероятность того, что он синий, равна 1/2*(11/25+12/17)
В первой урне 2 черных и 8 белых шаров. Во второй урне 3 белых и 7 черных шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар окажется белым, равна 0,55
В первой урне 3 белых и 7 черных шаров. Во второй урне 4 белых и 6 черных шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар окажется белым, равна 0,35
В первой урне 3 белых и 7 черных шаров. Во второй урне 6 белых и 4 черных шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар окажется белым, равна 0,45
В первой урне 2 белых и 8 черных шаров. Во второй урне 4 белых и 6 черных шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар окажется белым, равна 0,3
Вероятность появления события А в 20 независимых испытаниях, проводимых по схеме Бернулли, равна 0,95. Тогда математическое ожидание числа появлений этого события равно 19
Вероятность того, что дом может сгореть в течение года, равна 0,008. Застраховано 500 домов. Для вычисления вероятности того, что сгорит не более 6 домов, следует использовать Формулу Пуассона
Вероятность того, что дом может сгореть в течение года, равна 0,01. Застраховано 300 домов. Для вычисления вероятности того, что сгорит не более 4 домов, следует использовать Формулу Пуассона
Вероятность того, что дом может сгореть в течение года, равна 0,005. Застраховано 600 домов. Для вычисления вероятности того, что сгорит больше 2 домов, следует использовать Формулу Пуассона
Вероятность того, что дом может сгореть в течение года, равна 0,008. Застраховано 600 домов. Для вычисления вероятности того, что сгорит не более 5 домов, следует использовать Формулу Пуассона
| Выборочное уравнение парной регрессии имеет вид: y=4,4-2,2x, Тогда выборочный коэффициент корреляции может быть равен -0,9 |
Выборочное уравнение парной регрессии имеет вид: y=2,8+0,8х  , ,  . Тогда выборочный коэффициент корреляции равен 0,5 . Тогда выборочный коэффициент корреляции равен 0,5
|
Выборочное уравнение парной регрессии имеет вид: y=-3,2 +2,4x,  , ,  . Тогда выборочный коэффициент корреляции равен 0,8 . Тогда выборочный коэффициент корреляции равен 0,8
|
Выборочное уравнение парной регрессии имеет вид: y=1,2-0,8x,  , ,  . Тогда выборочный коэффициент корреляции равен -0,75 . Тогда выборочный коэффициент корреляции равен -0,75
|
Выборочное уравнение парной регрессии имеет вид: y=1,2-0,8x,  , ,  . Тогда выборочный коэффициент корреляции равен -0,75 . Тогда выборочный коэффициент корреляции равен -0,75
|
| Выборочное уравнение парной регрессии имеет вид: y=-2,8+1,4. Тогда выборочный коэффициент корреляции может быть равен 0,6 |
График плотности распределения вероятностей непрерывной случайной величины Х, распределённой равномерно в интервале  , имеет вид:
, имеет вид:  Тогда значение a равно 1/8
Тогда значение a равно 1/8
График плотности распределения вероятностей непрерывной случайной величины Х, распределённой равномерно в интервале  , имеет вид:
, имеет вид:  Тогда значение a равно 1/7
Тогда значение a равно 1/7
График плотности распределения вероятностей непрерывной случайной величины Х, распределённой равномерно в интервале 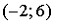 , имеет вид:
, имеет вид:  Тогда значение a равно 1/8
Тогда значение a равно 1/8
График плотности распределения вероятностей непрерывной случайной величины Х, распределённой равномерно в интервале  , имеет вид:
, имеет вид:  Тогда значение a равно 1/8
Тогда значение a равно 1/8
График плотности распределения вероятностей непрерывной случайной величины Х, распределённой равномерно в интервале 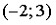 , имеет вид: , имеет вид:  Тогда значение а равно 0,2 Тогда значение а равно 0,2
|
График плотности распределения вероятностей непрерывной случайной величины Х, распределённой равномерно в интервале  , имеет вид:
, имеет вид:  Тогда значение a равно 1/7
Тогда значение a равно 1/7
График плотности распределения вероятностей непрерывной случайной величины Х, распределённой равномерно в интервале  , имеет вид:
, имеет вид:  Тогда значение а равно 0,25
Тогда значение а равно 0,25
График плотности распределения вероятностей  случайной величины приведен на рисунке.
случайной величины приведен на рисунке.  Тогда значение
Тогда значение  равно 1
равно 1
Два стрелка производят по одному выстрелу. Вероятности попадания в цель для первого и второго стрелков равны 0,9 и 0,3 соответственно. Тогда вероятность того, что в цель попадут оба стрелка, равна 0,27
Два стрелка производят по одному выстрелу. Вероятности попадания в цель для первого и второго стрелков равны 0,6 и 0,3 соответственно. Тогда вероятность того, что в цель попадут оба стрелка, равна 0,18
Два стрелка производят по одному выстрелу. Вероятности попадания в цель для первого и второго стрелков равны 0,8 и 0,3 соответственно. Тогда вероятность того, что в цель попадут оба стрелка, равна 0,24
Дан закон распределения вероятностей дискретной случайной величины Х:  Тогда значение a равно 0,1
Тогда значение a равно 0,1
Дискретная случайная величина задана законом распределения вероятностей:  Тогда её математическое ожидание равно 2,9 если a=0,3 b=0,6
Тогда её математическое ожидание равно 2,9 если a=0,3 b=0,6
Дан закон распределения вероятностей дискретной случайной величины Х: 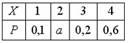 Тогда значение a равно 0,1
Тогда значение a равно 0,1
Дискретная случайная величина Х задана законом распределения вероятностей:  Тогда математическое ожидание случайной величины
Тогда математическое ожидание случайной величины  равно 13,8
равно 13,8
Дан закон распределения вероятностей дискретной случайной величины Х:  Тогда значение а равно 0,3
Тогда значение а равно 0,3
Дискретная случайная величина задана законом распределения вероятностей:  Тогда её математическое ожидание равно 1,9 если a=0,3 b=0,6
Тогда её математическое ожидание равно 1,9 если a=0,3 b=0,6
Дискретная случайная величина Х задана законом распределения вероятностей  Если математическое ожидание
Если математическое ожидание  , то значение х2 равно -1
, то значение х2 равно -1
Дискретная случайная величина Х задана законом распределения вероятностей:  Тогда математическое ожидание случайной величины
Тогда математическое ожидание случайной величины  равно 11,5
равно 11,5
Дан закон распределения вероятностей дискретной случайной величины Х:  Тогда значение а равно 0,1
Тогда значение а равно 0,1
Дискретная случайная величина Х задана законом распределения вероятностей  Тогда значение интегральной функции распределения вероятностей
Тогда значение интегральной функции распределения вероятностей  равно 0,2
равно 0,2
Дан закон распределения вероятностей дискретной случайной величины Х:  Тогда значение а равно 0,3
Тогда значение а равно 0,3
Дан закон распределения вероятностей дискретной случайной величины Х:  Тогда значение а равно 0,2
Тогда значение а равно 0,2
Дан закон распределения вероятностей дискретной случайной величины Х:  Тогда значение а равно 0,2
Тогда значение а равно 0,2
Дискретная случайная величина Х задана законом распределения вероятностей:  Тогда математическое ожидание случайной величины
Тогда математическое ожидание случайной величины  равно 6,6
равно 6,6
Дискретная случайная величина Х задана законом распределения вероятностей  Если математическое ожидание
Если математическое ожидание  , то значение х3 равно 5
, то значение х3 равно 5
Для выборки объема  вычислена выборочная дисперсия вычислена выборочная дисперсия  . Тогда исправленная дисперсия . Тогда исправленная дисперсия  для этой выборки равна 484 для этой выборки равна 484
| ||
Дана выборка объема n. Если каждый элемент выборки увеличится в 2 раза, то дисперсия 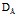 Увеличится в 4 раза Увеличится в 4 раза
| ||
Дана выборка объема n. Если каждый элемент выборки уменьшится на 8 единиц, то выборочное среднее  Уменьшится на 8 единиц Уменьшится на 8 единиц
| ||
Для выборки объема  вычислена выборочная дисперсия вычислена выборочная дисперсия  . Тогда исправленная дисперсия . Тогда исправленная дисперсия  для этой выборки равна 144 для этой выборки равна 144
| ||
Дана выборка объема n. Если каждый элемент выборки увеличить на 3 единицы, то дисперсия 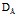 Не изменится
Не изменится
Дана выборка объема n. Если каждый элемент выборки уменьшить на 4 единицы, то выборочное среднее  Уменьшится на 4 единицы Уменьшится на 4 единицы
| |||
Если основная гипотеза имеет вид  , то конкурирующей может быть гипотеза H1: a≠20 , то конкурирующей может быть гипотеза H1: a≠20
| |||
Если основная гипотеза имеет вид  , то конкурирующей может быть гипотеза H1: a>14 , то конкурирующей может быть гипотеза H1: a>14
| |||
Если основная гипотеза имеет вид  , то конкурирующей может быть гипотеза H1: Ϭ2<2 , то конкурирующей может быть гипотеза H1: Ϭ2<2
| |||
Если основная гипотеза имеет вид 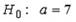 , то конкурирующей может быть гипотеза H1: a≠7 , то конкурирующей может быть гипотеза H1: a≠7
| |||
Если основная гипотеза имеет вид  , то конкурирующей может быть гипотеза H1: a≠13 , то конкурирующей может быть гипотеза H1: a≠13
| |||
Если основная гипотеза имеет вид  , то конкурирующей может быть гипотеза H1: Ϭ2≠3 , то конкурирующей может быть гипотеза H1: Ϭ2≠3
| |||
Если основная гипотеза имеет вид  , то конкурирующей может быть гипотеза H1: a≠19 , то конкурирующей может быть гипотеза H1: a≠19
| |||
Если основная гипотеза имеет вид  , то конкурирующей может быть гипотеза H1: a≠12 , то конкурирующей может быть гипотеза H1: a≠12
| |||
Если основная гипотеза имеет вид  , то конкурирующей может быть гипотеза H1: Ϭ2 >5 , то конкурирующей может быть гипотеза H1: Ϭ2 >5
| |||
Если основная гипотеза имеет вид  , то конкурирующей может быть гипотеза H1: a≠17 , то конкурирующей может быть гипотеза H1: a≠17
| |||
Если основная гипотеза имеет вид  , то конкурирующей может быть гипотеза H1: a≠18 , то конкурирующей может быть гипотеза H1: a≠18
| |||
Если основная гипотеза имеет вид  , то конкурирующей может быть гипотеза H1:p>0,4 , то конкурирующей может быть гипотеза H1:p>0,4
| |||
Если основная гипотеза имеет вид 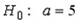 , то конкурирующей может быть гипотеза H1: a>5 , то конкурирующей может быть гипотеза H1: a>5
| |||
Если основная гипотеза имеет вид  , то конкурирующей может быть гипотеза H1:p≠0,2 , то конкурирующей может быть гипотеза H1:p≠0,2
| |||