Из урны, в которой находятся 5 белых и 7 черных шаров, вынимают наудачу один шар. Тогда вероятность того, что этот шар будет белым, равна 5/12
Игральная кость бросается один раз. Тогда вероятность того, что на верхней грани выпадет менее трех очков, равна 1/3
Из урны, в которой находятся 5 белых и 9 черных шаров, вынимают наудачу один шар. Тогда вероятность того, что этот шар будет белым, равна 5/14
Игральная кость бросается один раз. Тогда вероятность того, что на верхней грани выпадет 4 очка, равна 1/6
Игральная кость бросается один раз. Тогда вероятность того, что на верхней грани выпадет не более трех очков, равна 1/2
Игральная кость бросается один раз. Тогда вероятность того, что на верхней грани выпадет 3 очка, равна 1/6
Из урны, в которой находятся 4 белых и 9 черных шаров, вынимают наудачу один шар. Тогда вероятность того, что этот шар будет белым, равна 4/13
Из каждой из двух колод вынимают по одной карте. События А – «карта из первой колоды – красной масти» и В – «карта из второй колоды – бубновой масти» являются: независимыми, совместными
Игральная кость бросается один раз. Тогда вероятность того, что на верхней грани выпадет более двух очков, равна 2/3
Из урны, в которой находятся 5 белых и 7 черных шаров, вынимают наудачу один шар. Тогда вероятность того, что этот шар будет белым, равна 5/12
Имеются две одинаковые на вид урны. В первой урне находятся два зеленых и два черных шара. Во второй урне - четыре красных и один черный шар. Из наудачу взятой урны взяли один шар. Тогда вероятность того, что этот шар черный равна 7/20
Из генеральной совокупности извлечена выборка объема 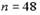 , полигон частот которой имеет вид:  Тогда число вариант  в выборке равно 9
| |
Из генеральной совокупности извлечена выборка объема n=50, полигон частот которой имеет вид  Тогда число вариант xi=4 в выборке равно 15
|
Из генеральной совокупности извлечена выборка объема 
, полигон частот которой имеет вид: 
Тогда число вариант 
в выборке равно 13
|
|
Из генеральной совокупности извлечена выборка объема  , полигон частот которой имеет вид: 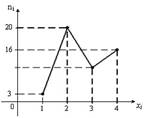 Тогда число вариант в выборке равно 11
|
Из генеральной совокупности извлечена выборка объема n=40, полигон частот которой имеет вид 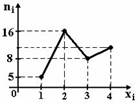 Тогда число вариант xi=4 в выборке равно 11
|
Из генеральной совокупности извлечена выборка объема n=60, полигон частот которой имеет вид 
Тогда число вариант xi=2 в выборке равно 34
Из генеральной совокупности извлечена выборка объема 
, полигон частот которой имеет вид: 
Тогда число вариант в выборке равно 14
Из генеральной совокупности извлечена выборка объема n=50:  Тогда n4 равен 23
|
Из генеральной совокупности извлечена выборка объема n=70, полигон частот которой имеет вид  Тогда число вариант xi=1 в выборке равно 7
|
Из генеральной совокупности извлечена выборка объема n=50:  Тогда n1 равен 26
|
Из генеральной совокупности извлечена выборка объема n=50:  Тогда n2 равен 19
|
Мода вариационного ряда 
равна 4
Мода вариационного ряда равна 5
Мода вариационного ряда 5, 8, 8, 9, 10, 11, 13 равна 8
Мода вариационного ряда 2, 3, 4, 8, 9, 9, 10 равна 9
Мода вариационного ряда равна 2