Мода вариационного ряда равна 3
Мода вариационного ряда 2, 5, 5, 6, 7, 9, 10 равна 5
Мода вариационного ряда равна 6
Мода вариационного ряда 1, 2, 3, 4, 5, 5, 7 равна 5
Мода вариационного ряда 2, 5, 5, 6, 7, 9, 10 равна 5
Мода вариационного ряда равна 1
Мода вариационного ряда 1, 2, 5, 6, 7, 7, 10 равна 7
Мода вариационного ряда равна 3
Мода вариационного ряда 2, 3, 4, 7, 8, 8, 9 равна 8
Мода вариационного ряда равна 1
Мода вариационного ряда равна 2
Мода вариационного ряда 1, 2, 5, 6, 7, 7, 10 равна 7
Мода вариационного ряда 3, 4, 5, 6, 10, 10, 12 равна 10
Мода вариационного ряда 4, 7, 7, 8, 9, 11, 12 равна 7
Мода вариационного ряда равна 4
Несовместные события  ,
,  ,
,  не образуют полную группу, если их вероятности равны
не образуют полную группу, если их вероятности равны
P(A)=1/7, P(B)=2/7, P(C)=5/7
P(A)=1/12, P(B)=3/4, P(C)=1/4
Несовместные события  ,
,  ,
,  не образуют полную группу, если их вероятности равны
не образуют полную группу, если их вероятности равны
P(A)=3/7, P(B)=1/7, P(C)=5/7 P(A)=5/12, P(B)=1/4, P(C)=1/4
Несовместные события  ,
,  ,
,  не образуют полную группу, если их вероятности равны
не образуют полную группу, если их вероятности равны
P(A)=1/6, P(B)=2/5, P(C)=1/7 P(A)=1/7, P(B)=1/3, P(C)=1/3
Несовместные события  ,
,  ,
,  не образуют полную группу, если их вероятности равны
не образуют полную группу, если их вероятности равны
P(A)=1/3, P(B)=1/4, P(C)=1/4 P(A)=3/8, P(B)=1/8, P(C)=2/7
Несовместные события  ,
,  ,
,  не образуют полную группу, если их вероятности равны
не образуют полную группу, если их вероятности равны
P(A)=1/3, P(B)=1/4, P(C)=1/2
Непрерывная случайная величина X задана плотностью распределения вероятностей  .Тогда математическое ожидание этой нормально распределённой случайной величины равно 12 .Тогда математическое ожидание этой нормально распределённой случайной величины равно 12
|
Непрерывная случайная величина Х задана интегральной функцией распределения вероятностей  Тогда значение С равно 0 Тогда значение С равно 0
|
Непрерывная случайная величина Х задана интегральной функцией распределения вероятностей  Тогда значение С равно 0 Тогда значение С равно 0
|
Непрерывная случайная величина X задана плотностью распределения вероятностей  .Тогда математическое ожидание этой нормально распределённой случайной величины равно 6
.Тогда математическое ожидание этой нормально распределённой случайной величины равно 6
Непрерывная случайная величина Х задана интегральной функцией распределения вероятностей  Тогда значение дифференциальной функции распределения вероятностей этой случайной величины в точке Тогда значение дифференциальной функции распределения вероятностей этой случайной величины в точке  равно 1/2 равно 1/2
| ||||
Непрерывная случайная величина Х задана интегральной функцией распределения вероятностей  Тогда значение дифференциальной функции распределения вероятностей этой случайной величины в точке Тогда значение дифференциальной функции распределения вероятностей этой случайной величины в точке  равно 2,2 равно 2,2
|
По мишени производится четыре выстрела. Значение вероятности промаха при первом выстреле 0,4; при втором - 0,5; при третьем – 0,5; при четвертом – 0,2. Тогда вероятность того, что мишень не будет поражена ни разу равна 0,02
По мишени производится четыре выстрела. Значение вероятности промаха при первом выстреле 0,3; при втором – 0,8; при третьем – 0,5; при четвертом – 0,8. Тогда вероятность того, что мишень будет поражена все четыре раза, равна 0,014
При бросании точки на плоскость достоверно ее попадание в круг площади S; попадание в любую точку круга равновероятно. Вероятность ее попадания в концентрический круг площади s равна P(A)=s/S
По мишени производится три выстрела. Значение вероятности ни одного попадания при всех трех выстрелах равно 0,5; значение вероятности ровно одного попадания - 0,3; значение вероятности ровно двух попаданий – 0,15. Тогда значение вероятности того, что мишень будет поражена не менее двух раз будет равно 0,45
По мишени производится четыре выстрела. Значение вероятности промаха при первом выстреле 0,3; при втором - 0,3; при третьем – 0,5; при четвертом – 0,4. Тогда вероятность того, что мишень не будет поражена ни разу равна 0,018
Пусть X – дискретная случайная величина, заданная законом распределения вероятностей:  Тогда математическое ожидание этой случайной величины равно 1,6
Тогда математическое ожидание этой случайной величины равно 1,6
Пусть X – дискретная случайная величина, заданная законом распределения вероятностей:  Тогда математическое ожидание этой случайной величины равно 0,8
Тогда математическое ожидание этой случайной величины равно 0,8
Пусть X – дискретная случайная величина, заданная законом распределения вероятностей:  Тогда математическое ожидание этой случайной величины равно 3,8
Тогда математическое ожидание этой случайной величины равно 3,8
Пусть X – дискретная случайная величина, заданная законом распределения вероятностей:  Тогда математическое ожидание этой случайной величины равно 2
Тогда математическое ожидание этой случайной величины равно 2
Пусть X – дискретная случайная величина, заданная законом распределения вероятностей:  Тогда математическое ожидание этой случайной величины равно 3,2
Тогда математическое ожидание этой случайной величины равно 3,2
По выборке объема n=100 построена гистограмма частот:  Тогда значение а равно 5
Тогда значение а равно 5
По выборке объема n=100 построена гистограмма частот:  Тогда значение а равно 4 Тогда значение а равно 4
|
По выборке объема n=100 построена гистограмма частот:  Тогда значение а равно 12 Тогда значение а равно 12
|
По выборке объема n=100 построена гистограмма частот:  Тогда значение а равно 6
Тогда значение а равно 6
Проведено четыре измерения (без систематических ошибок) некоторой случайной величины (в мм): 3, 8, 9, 16. Тогда несмещенная оценка математического ожидания равна 9
| Проведено 5 измерений (без систематических ошибок) некоторой случайной величины (в мм): 6, 7, 8, 10, 11. Тогда несмещенная оценка математического ожидания равна 8,4 | ||
| Проведено четыре измерения (без систематических ошибок) некоторой случайной величины (в мм): 4, 5, 6, 9. Тогда несмещенная оценка математического ожидания равна 6 | ||
| Проведено четыре измерения (без систематических ошибок) некоторой случайной величины (в мм): 2, 3, 6, 9. Тогда несмещенная оценка математического ожидания равна 5 | ||
| Проведено четыре измерения (без систематических ошибок) некоторой случайной величины (в мм): 4, 7, 8, 9. Тогда несмещенная оценка математического ожидания равна 7 Проведено четыре измерения (без систематических ошибок) некоторой случайной величины (в мм): 3, 5, 8, 9. Тогда несмещенная оценка математического ожидания равна 6,25 | ||
Проведено 5 измерений (без систематических ошибок) некоторой случайной величины (в мм): 9, 10, 13, 14, 15. Тогда несмещенная оценка математического ожидания равна 12,2
| Проведено четыре измерения (без систематических ошибок) некоторой случайной величины (в мм): 2, 3, 7, 9. Тогда несмещенная оценка математического ожидания равна 5,25 |
| Проведено четыре измерения (без систематических ошибок) некоторой случайной величины (в мм): 8, 9, 10, 13. Тогда несмещенная оценка математического ожидания равна 10 |
Событие А может наступить лишь при условии появления одного из двух несовместных событий B1 и B2, образующих полную группу событий. Известны вероятность  и условные вероятности
и условные вероятности 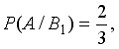
 . Тогда вероятность
. Тогда вероятность  равна 7/18
равна 7/18
Событие А может наступить лишь при условии появления одного из двух несовместных событий B1 и B2, образующих полную группу событий. Известны вероятность  и условные вероятности
и условные вероятности 
 . Тогда вероятность
. Тогда вероятность  равна 3/7
равна 3/7
Событие А может наступить лишь при условии появления одного из двух несовместных событий B1 и B2, образующих полную группу событий. Известны вероятность  и условные вероятности
и условные вероятности 
 . Тогда вероятность
. Тогда вероятность  равна 2/5
равна 2/5
Событие А может наступить лишь при условии появления одного из двух несовместных событий B1 и B2, образующих полную группу событий. Известны вероятность  и условные вероятности
и условные вероятности 
 . Тогда вероятность
. Тогда вероятность  равна 5/8
равна 5/8
Страхуется 1200 автомобилей; считается, что каждый из них может попасть в аварию с вероятностью 0.08. Для вычисления вероятности того, что количество аварий среди всех застрахованных автомобилей не превзойдет 100, следует использовать Интегральную формулу Муавра-Лапласа
Случайная величина  распределена равномерно на отрезке
распределена равномерно на отрезке  . Случайная величина
. Случайная величина  имеет Равномерное распределение на отрезке [7;19]
имеет Равномерное распределение на отрезке [7;19]
Случайная величина  задана плотностью распределения вероятностей:
задана плотностью распределения вероятностей:  Тогда соответствующая функция распределения вероятностей равна
Тогда соответствующая функция распределения вероятностей равна 
Случайная величина  распределена равномерно на отрезке распределена равномерно на отрезке  . Распределение случайной величины . Распределение случайной величины  имеет Равномерное распределение на отрезке [-1;9] имеет Равномерное распределение на отрезке [-1;9]
| ||
Случайная величина  распределена равномерно на отрезке распределена равномерно на отрезке  . Случайная величина . Случайная величина  имеет Равномерное распределение на отрезке [-10;5] имеет Равномерное распределение на отрезке [-10;5]
| ||
Случайная величина  распределена равномерно на отрезке распределена равномерно на отрезке 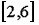 . Случайная величина . Случайная величина 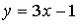 имеет Равномерное распределение на отрезке [5;17] имеет Равномерное распределение на отрезке [5;17]
| ||
Случайная величина  распределена равномерно на отрезке
распределена равномерно на отрезке  . Тогда случайная величина
. Тогда случайная величина  имеет Равномерное распределение на отрезке [8;18]
имеет Равномерное распределение на отрезке [8;18]
Случайная величина  распределена равномерно на отрезке
распределена равномерно на отрезке  .. Распределение случайной величины
.. Распределение случайной величины 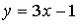 имеет Равномерное распределение на отрезке [-10;17]
имеет Равномерное распределение на отрезке [-10;17]
Статистическое распределение выборки имеет вид  Тогда относительная частота варианты
Тогда относительная частота варианты  , равна 0,2
, равна 0,2
Статистическое распределение выборки имеет вид  Тогда относительная частота варианты
Тогда относительная частота варианты  , равна 0,3
, равна 0,3
Статистическое распределение выборки имеет вид  Тогда относительная частота варианты Тогда относительная частота варианты  , равна 0,3 , равна 0,3
|
Статистическое распределение выборки имеет вид 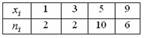 Тогда относительная частота варианты Тогда относительная частота варианты  , равна 0,5 , равна 0,5
|
Статистическое распределение выборки имеет вид  Тогда относительная частота варианты
Тогда относительная частота варианты  , равна 0,2
, равна 0,2
 .Тогда математическое ожидание этой нормально распределённой случайной величины равно 10
.Тогда математическое ожидание этой нормально распределённой случайной величины равно 10
 .Тогда математическое ожидание этой нормально распределённой случайной величины равно 13
.Тогда математическое ожидание этой нормально распределённой случайной величины равно 13
 Тогда значение С равно 0
Тогда значение С равно 0
 Тогда значение дифференциальной функции распределения вероятностей этой случайной величины в точке
Тогда значение дифференциальной функции распределения вероятностей этой случайной величины в точке  равно 2/3
равно 2/3