Лекция №17.Магнитные цепи.
Образовательные результаты по ФГОС:
Знать: классификацию электронных приборов, их устройство и область применения;
методы расчета и измерения основных параметров электрических цепей; основные законы электротехники; основные правила эксплуатации электрооборудования и методы измерения электрических величин; основы теории электрических машин, принцип работы типовых электрических устройств; параметры электрических схем и единицы их измерения;
принцип выбора электрических и электронных приборов; принципы составления простых электрических и электронных цепей; способы получения, передачи и использования электрической энергии; устройство, принцип действия и основные характеристики электротехнических приборов;
основы физических процессов в проводниках, полупроводниках и диэлектриках; характеристики и параметры электрических и магнитных полей, параметры различных электрических цепей.
Уметь: выбирать электрические, электронные приборы и электрооборудованиеправильно эксплуатировать электрооборудование и механизмы передачи движения технологических машин и аппаратов; производить расчеты простых электрических цепей; рассчитывать параметры различных электрических цепей и схем; снимать показания и пользоваться электроизмерительными приборами и приспособлениями.
Задание: составить конспект лекции, выделить главное, ответить на контрольные вопросы.
План.
Тема:1. Методы расчёта магнитных цепей постоянного и переменного тока.
2.Пример расчета магнитных цепей.
Методы расчёта магнитных цепей постоянного и переменного тока.
Суть рассчёта сводится к определению основных параметров магнитных цепей: Н, Ф, В, I, S. При этом пользуются понятиями магнитодвижущей силы, закона полного тока, магнитного напряжения 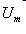 и магнитного сопротивления
и магнитного сопротивления 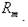 .
.
|
|
Если по намагничивающей обмотке протекает ток I, то магнитодвижущей силой обмотки F называют произведение величины тока на число витков:

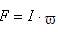 (1)
(1)
Связь между магнитодвижущей силой F и напряженностью магнитного поля Н устанавливает закон полного тока:
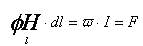 (2)
(2)
При анализе магнитных цепей пользуются значением средней линии магнитопровода, поэтому
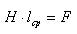 (3)
(3)
Произведение
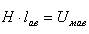 (4)
(4)
называют магнитным напряжением участка цепи длиной ав.
Если магнитная цепь содержит два неоднородных участка длиной 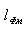 и
и 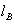 , то
, то
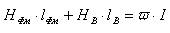
или
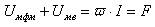 (5)
(5)
Таким образом алгебраическая сумма магнитных напряжений на участках цепи равна магнитодвижущей силе обмотки. Выражение (5) представляет собой второй закон Кирхгофа для магнитной цепи.
Аналогично первого закона Кирхгофа является теорема Гауса: поток вектора магнитной индукции через любую замкнутую поверхность равен нулю:

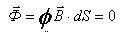 (6)
(6)
Рассмотрим выражение для магнитногонапряжения
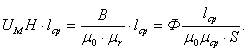
Обозначим выражение
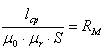
 называется магнитным сопротивлением.
называется магнитным сопротивлением.
Тогда
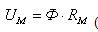 (7)
(7)
Равенство (7) представляет собой закон Ома для магнитной цепи.
Если основной характеристикой электрической цепи является вольт-амперная характеристика, то для магнитной цепи - это ампер-веберная характеристика - зависимость между магнитным потоком и намагничивающим током 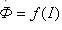 (рисунок 1).
(рисунок 1).
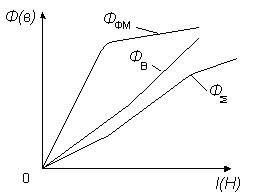
Рисунок 1 - Ампер-веберная характеристика - зависимость между магнитным потоком и намагничивающим током
На рисунке 1 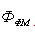 - поток в ферромагнитном материале,
- поток в ферромагнитном материале, 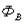 - поток в воздушном зазоре,
- поток в воздушном зазоре, 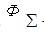 - результирующий поток.
- результирующий поток.
|
|
На практике используется зависимость 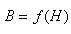 , так как Н пропорциональна намагничивающему току I, а В пропорциональна магнитному потоку Ф.
, так как Н пропорциональна намагничивающему току I, а В пропорциональна магнитному потоку Ф.
При анализе магнитных цепей переменного тока вводят следующие допущения:
- магнитное поле рассеяния отсутствует;
- активное сопротивление обмотки равно нулю.
При таких допущениях можно записать
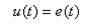
где 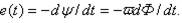
Отсюда следует, что магнитный поток в магнитопроводе переменный и определяется напряжением (воздействием)
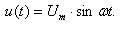
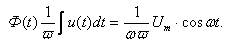 (8)
(8)
Таким образом, закон изменения магнитного потока Ф(t) не зависит от параметров цепи. Это первая особенность магнитных цепей переменного тока. Чтобы определить вторую особенность обратимся к известному выражению
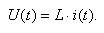
Из него следует, что
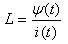 (9)
(9)
Но для простейшей магнитной цепи справедливы уравнения:
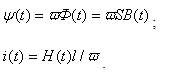
Переменные В(t) и Н(t) связаны по закону динамической петли гистерезиса. Эта связь нелинейна. Значит зависимость (9) тоже нелинейна, а индуктивность
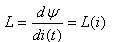
переменна. Это вторая особенность.
Индуктивность обмотки магнитопровода непостоянна и зависит от тока цепи, а уравнение
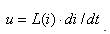
нелинейно. Отсюда третья особенность: магнитные цепи являются нелинейными цепями, поэтому при синусоидальном напряжении на обмотке ток в ней оказывается несинусоидальным.
Изменение магнитного потока Ф(t) c частотой w приводит к нагреву магнитопровода из-за гистерезиса. Следовательно, в магнитопроводе возникают потери электроэнергии. Их называют магнитными потерями. Это четвертая особенность.