Данные операции также определены только для квадратных матриц. Чтобы возвести квадратную матрицу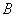 
в куб, нужно вычислить произведение:
Фактически это частный случай умножения трёх матриц, по свойству ассоциативности матричного умножения: 
. А матрица, умноженная сама на себя – это квадрат матрицы: 
Таким образом, получаем рабочую формулу: 
То есть задание выполняется в два шага: сначала матрицу необходимо возвести в квадрат, а затем полученную матрицу 
умножить на матрицу .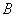
Пример 8
Возвести матрицу 
в куб.
Это небольшая задачка для самостоятельного решения.
Возведение матрицы в четвёртую степень проводится закономерным образом:
Используя ассоциативность матричного умножения, выведем две рабочие формулы. Во-первых: 
– это произведение трёх матриц.
1) 
. Иными словами, сначала находим 
, затем домножаем его на «бэ» – получаем куб, и, наконец, выполняем умножение ещё раз – будет четвёртая степень.
2) Но существует решение на шаг короче: 
. То есть, на первом шаге находим квадрат и, минуя куб, выполняем умножение 
Дополнительное задание к Примеру 8:
Возвести матрицу в четвёртую степень.
Как только что отмечалось, сделать это можно двумя способами:
1) Коль скоро известен куб, то выполняем умножение 
.
2) Однако, если по условию задачи требуется возвести матрицу только в четвёртую степень, то путь выгодно сократить – найти квадрат матрицы и воспользоваться формулой 
.
Оба варианта решения и ответ – в конце урока.
Аналогично матрица возводится в пятую и более высокие степени. Из практического опыта могу сказать, что иногда попадаются примеры на возведение в 4-ю степень, а вот уже пятой степени что-то не припомню. Но на всякий случай приведу оптимальный алгоритм:
1) находим ;
2) находим ;
3) возводим матрицу в пятую степень: 
.
Вот, пожалуй, и все основные свойства матричных операций, которые могут пригодиться в практических задачах.
Во втором разделе урока ожидается не менее пёстрая тусовка.
Матричные выражения
Повторим обычные школьные выражения с числами. Числовое выражение состоит из чисел, знаков математических действий и скобок, например: 
. При расчётах справедлив знакомый алгебраический приоритет: сначала учитываются скобки, затем выполняется возведение в степень / извлечение корней, потом умножение / делениеи в последнюю очередь – сложение /вычитание.
Если числовое выражение имеет смысл, то результат его вычисления является числом, например:
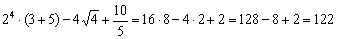
Матричные выражения устроены практически так же! С тем отличием, что главными действующими лицами выступают матрицы. Плюс некоторые специфические матричные операции, такие, как транспонирование и нахождение обратной матрицы.
Рассмотрим матричное выражение 
, где 
– некоторые матрицы. В данном матричном выражении три слагаемых и операции сложения/вычитания выполняются в последнюю очередь.
В первом слагаемом 
сначала нужно транспонировать матрицу «бэ»: 
, потом выполнить умножение 
и внести «двойку» в полученную матрицу. Обратите внимание, что операция транспонирования имеет более высокий приоритет, чем умножение. Скобки, как и в числовых выражениях, меняют порядок действий: 
– тут сначала выполняется умножение 
, потом полученная матрица транспонируется и умножается на 2.
Во втором слагаемом 
в первую очередь выполняется матричное умножение 
, и обратная матрица находится уже от произведения. Если скобки убрать: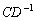 
, то сначала необходимо найти обратную матрицу 
, а затем перемножить матрицы: 
. Нахождение обратной матрицы также имеет приоритет перед умножением.
С третьим слагаемым 
всё очевидно: возводим матрицу в куб и вносим «пятёрку» в полученную матрицу.