I блок
1. Теорема Больцано-Вейерштрасса и критерий Коши для числовых последовательностей.
2. Числовые последовательности и свойствасходящихся числовых последовательностей.
3. Понятие функций. Предел и непрерывность функций.
4. Свойства непрерывных функции на отрезке.
5. Теоремы Ролля, Лагранжа, Коши.
6. Формула Тейлора для функции одной переменной.
7. Понятие определенного интеграла.
8. Теорема о среднем для определенного интеграла.
9. Числовые ряды. Сходимость числовых рядов их свойства.
10. Фунциональные и степенные ряды.
11. Необходимое усовие сходимости функциональных рядов.
12. Криволинейные и поверхностные интегралы. Формула Грина.
13. Метрическое пространство. Непрерывные отображения в метрическом пространстве.
14. Изометрия. Компактность в метрическом пространстве.
15. Пополнение метрического пространства. Принцип сжимающих отображений в метрическом пространстве.
16. Линейное нормированное пространство. Примеры.
17. Линейные функционалы.
18. Банаховы и гильбертовы пространства. Примеры.
19. Линейные операторы. Обратные операторы и их свойства.
20. Векторные функций со скалярными аргументами.
21. Огибающая семейства кривых, зависящих от параметра.
22. Длина дуги кривой. Кривизна кривой. Кручение кривой.
23. Элементарная поверхность. Общая поверхность. Регулярная поверхность. Особые точки на регулярной поверхности.
24. Касательная плоскость поверхности.
25. Длина кривой на поверхности. Угол между кривыми на поверхности. Площадь поверхности.
26. Кривизна кривой, лежащей на поверхности. Асимтотические направления. Асимптотические линии. Сопряженные напрвления.
II блок
27. Прямые методы решения СЛАУ. Метод Гаусса. Существование и устойчивость решении. Метод квадратичных корней. Метод Холецкого. LU-разложение.
28. Общая схема решения СЛАУ итерационным методом. Метод простой итерации. Метод Зейделя. Метод сопряжённых градиентов.
29. Интерполяционные формулы Ньютона, Гаусса, Стирлинга-Бесселя, Лагранжа. Оценки погрешности интерполяционных формул.
30. Разностные уравнения и их решения. Разностные сетки и сеточные функции.
31. Конечно-разностные схемы. Аппроксимация, сходимость и устойчивость. Сходимость как следствие аппроксимации и устойчивости.
32. Существование решения краевых задач трехточечных разностных уравнении. Метод прогонки.
33. Задача Коши для уравнений теплопроводности. Численные методы решения начально-краевых задач для уравнений теплопроводности.
34. Матрицы. Основные операции над матрицами и их свойства.
35. Опредители и их свойства.
36. Определитель суммы и произведения матриц. Понятие обратной матрицы.
37. Алгебраическое дополнение, ранг и миноры матрицы. Теорема о базисном миноре матрицы.
38. Общие методы решения систем линейных алгебраических уравнений. Теорема Кронекера-Капелли.
39. Пониятие линейного пространства. Базис. Размерность подпространства.
40. Вешественное и комплексное Евклидово пространство, Неравенство Коши-Буняковского.
41. Линейный оператор и его свойства. Собственые значения и собственые векторы линейных операторов.
42. Сопряженные операторы и их свойства.
43. Унитарные и нормальные операторы.
44. Билинейные и квадратичные формы. Приведение квадратичной формы к каноническому виду.
45. Понятие вектора и линейных операции над векторами. Линейно независимыем, линейные зависимые системы векторов, базис, система аффинных координат, координата точки.
46. Скалярное, векторное, смешанное произведения двух векторов.
47. Уравнения линии на плоскости, расстояние от точки до прямой, взаиморасположение прямых на плоскости.
48. Уравнение линии в пространстве и их взаимные расположения порядка в пространстве.
49. Уравнение плоскостей на трехмерных пространства и их взаимные расположения.
50. Поверхности второго порядка в пространстве, их общее уравнение и простое уравнение, классификация поверхносей второго порядка в пространстве.
51. Поверхности второго порядка в пространстве, классификация поверхностей второго порядка, классификация центральных поверхностей.
52. Теорема о полярном разложении линейных операторов.
III блок
53. Теорема о спектральном разложении самосопряженных операторов.
54. Приведение матрицы к Жордановой форме.
55. Основные понятия дифференциальных уравнений. Дифференциальные уранения с разделяющимися переменнными.
56. Однородные дифференциальные уранения. Линейные дифференциальные уранения первого порядка.
57. Теорема существования и единственности задачи Коши для дифференциального уравнения.
58. Полные дифференциальные уравнения, интегральный множитель.
59. Фундаментальная система решений однородного дифференцального уравнения n-го порядка с постоянными коэффициентами.
60. Неоднородное линейное дифференцальное уравнение n-го порядка с постоянными коэффициентами.
61. Общие свойства линейных дифференциальных уравнений, линейная зависимость и линейная независимость системы функций.
62. Системы однородных линейных дифференциальных уравнений, свойства решении.
63. Формула Лиувилля-Остроградского.
64. Неоднородые линейные системы дифференциальных уравнении. Метод вариациипостоянных.
65. Классификация уравнений в частных производных II порядка и их канонические формы.
66. Постановка задачи Коши и начально-краевых задач для гиперболических уравнений второго порядка.
67. Общий вид решения для уравнения колебаний струны.
68. Задача Коши для волнового уравнения на пространстве R³, формула Кирхгофа.
69. Метод разделения переменных для волнового уравнения.
70. Постановка задачи Коши и начально-краевых задач для параболических уравнений второго порядка.
71. Принцип максимума для параболических уравнений.
72. Неоднородное уравнение теплопроводности, решение методом Фурье.
73. Граничные задачи для уравнений Лапласа. Принцип максимума.
74. Общие свойства гармонических функций. Формулы Грина.
75. Пусть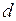 
метрика. Покажите, что функция 
определенная равенством 
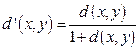также является метрикой.
76. Показать, что пространство непрерывных функций на отрезке 
не является Евклидовым (указание: положим 
.)
77. Пусть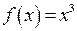 
определена на промежутке 
. Применяя теорему о среднем значении для интеграла определить среднее значение данной функций в этом промежутке.
78. Показать, что 
функциональная последовательность не является фундаментальной в метрическом пространтсве 
.
79. Доказать, что любое нормированное пространство является метрическим пространством.
80. Оператор 
задаваемый формулой 
переводит пространство непрерывных на отрезке 
функции в себя, а также является в 
сжимающим отображением. Доказать.
81. Множество непрерывных функции на отрезке 
образует нормированное пространство, обозначим его через 
. Показать, что это пространство является полным пространством.
82. Последовательность {xn} такова, что ее подпоследовательности {x2n+1}, {x2n} сходятся. Верно ли, что сходится и сама последовательность {xn}?
83. Последовательность {xn} такова, что ее подпоследовательности {x2n+1}, {x2n}, {x3n} сходятся. Доказать, что тогда сходится и сама последовательность {xn}.
84. Пусть последовательность {xn} сходится, а последовательность {yn} получается из нее перестановкой. Доказать, что {yn} тоже сходится, причем к тому же пределу, что и исходная последовательность.
85. Функция f непрерывна на всей оси и удовлетворяет равенству 2f(x)=f(x/2) при всех x. Доказать, что f - тождественно нулевая функция.
86. Найти все α, модуль которых меньше двух, при которых найдется ненулевая непрерывно дифференцируемая на оси функция, удовлетворяющая равенству f(x)=αf(x/2) при всех x.
87. Функция f выпукла на всей оси и неположительна. Доказать, что она постоянна на оси.
88. Функции f и g дифференцируемы на оси и монотонны. Какие из следующих функций гарантированно будут монотонными: сумма, произведение, композиция этих функций.
89. Может ли сумма двух периодических функций быть непериодической.
90. Привести пример функции, отличной от постоянной, для которой каждое рациональное число является периодом.
91. Доказать, что на интервале (0;1) функцию sin(1/x) нельзя представить в виде разности двух неубывающих ограниченных функций, но можно на любом интервале (e;1) при положительном e.
92. Пусть fнепрерывна на отрезке [a;b], который разбит на конечное число отрезков точками a=x0<x1<…<xn=b. Доказать, что можно выбрать точки xiÎ(xi-1; xi-1) так, что интеграл функции f по отрезку [a;b] равен интегральной сумме f(x1)Dx1+ f(x2)Dx2+… f(xn)Dxn. Доказать, что это верно и для функций f, имеющих первообразную на [a;b].
93. Привести пример функции, модуль которой интегрируем по Риману, но сама функция – нет.
94. Доказать, что функция f, принимающая нулевое значение в иррациональных точках и значение равное 1/q, в точках x=p/q, если эта дробь несократима, является интегрируемой по Риману на отрезке [0;1].
95. Разложить функцию f(x)=sin2x в ряд Фурье по стандартной тригонометрической системе на отрезке [-π;π].
96. Разложить в ряд Тэйлора по степеням x функцию arctgx. Определить радиус сходимости полученного ряда.
97. Функция f непрерывна на всей оси и для каждого положительного e существует такой полином P, что модуль разности f-P принимает значения, меньшие e. Доказать, что f – полином.
98. Полином P таков, что на его графике можно отметит четыре точки, являющиеся вершинами квадрата. Доказать, что его степень не меньше трех.