Импульсная функция и интегралы Дюамеля
Пусть задан некоторый линейный дифференциальный оператор Ly с правой частью х (t)
 .
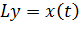| (13.2.1) |
В случае колебаний линейного одностепенного осциллятора
| (13.2.2) |
Импульсной функцией этого оператора является реакция системы h (t-t) на внешнее воздействие в момент времени t в виде дельта функции d(t-t)
 .
| (13.2.3) |
Решение уравнения (13.2.1) выражается через импульсную функцию h (t) из (13.2.3) в виде интегралов Дюамеля (13.2.4) и (13.2.5):
| (13.2.4) |
| (13.2.5) |
Нетрудно убедиться, что обе записи интегралов Дюамеля эквивалентны.
Сделав замену в (13.2.4) (4а) t-t=x и dt=- dx и, поменяв пределы интегрирования, приходим к выражению (13.2.5).
Проверим, что функции (13.2.4) и(13.2.5) являются решениями уравнения (13.2.1). Подставляя y (t) из (13.2.4) в уравнение (13.2.1) и учитывая равенство (13.2.3) и свойства дельта функции d(t), получим
| (13.2.6) |
Таким образом, дополнительно убеждаемся в представимости частного решения уравнения (13.2.1) в виде интегралов Дюамеля (13.2.4) и (13.2.5).
Для определения импульсной функции линейного осциллятора удобнее задачу, представленную в форме (13.2.3), несколько трансформировать.
Воздействие силы в виде d (t)–функции в правой части уравнения (13.2.3) заменяется импульсным воздействием 
на единичную массу (m =1),
где
При этом единичная масса приобретает начальную скорость, равную 1 в момент времени t, так как 
В результате исходная задача (13.2.3) трансформируется в следующую:
решается однородное уравнение
 
| (13.2.7) |
с начальными условиями
| (13.2.8) |
Нетрудно убедиться, что решение этой задачи (импульсная функция) имеет вид
| (13.2.9) |
здесь
Передаточная функция
По определению передаточной функцией линейного оператора (13.2.1) называется отношение амплитуды выходного процесса к амплитуде входа при внешнем гармоническом воздействии 
.
|
|
| (13.3.1) |
Очевидно, что решение y (t) в случае линейного оператора L будет иметь вид
| (13.3.2) |
Подставляя в уравнение (13.2.1) выражение для y в форме (13.3.2), будем иметь
| (13.3.3) |
В случае одностепенного осциллятора (13.2.2)
| (13.3.4) |
Таким образом, передаточная функция оператора L (13.2.2) запишется так
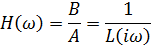
| (13.3.5) |
Связь между импульсной и передаточной функциями
Для установления связи между импульсной функцией d (t) уравнения (13.2.3) и передаточной функцией H (w) (13.3.5) применим преобразование Фурье к правой и левой частям уравнения (13.2.3)
| (13.4.1) |
Правая часть равенства (13.4.1) с учетом свойства d-функции преобразуется так:
| (13.4.2) |
В левую часть под знак интеграла входит выражение
| (13.4.3) |
Проиллюстрируем применение преобразования Фурье к первой и второй производным импульсной функции 
.
Проведем замену переменной t, по которой ведется интегрирование при применении преобразования Фурье к первой производной 
, на 
.
Тогда
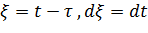
| (13.4.4) |
и, соответственно,
| (13.4.5) |
Затем проинтегрируем по частям интеграл в правой части (13.4.5)
| (13.4.6) |
Особенность импульсной функции h (x) в физике и, в частности, в механике заключается в том, что она затухает на бесконечности (функция и ее производная стремятся на бесконечности к нулю). Поэтому внеинтегральные члены в (13.4.6) равны нулю.
Окончательно преобразование Фурье от первой производной импульсной функции принимает вид
| (13.4.7) |
Нетрудно убедиться, проведя двукратное интегрирование по частям, что преобразование Фурье второй производной импульсной функции приведет к равенству
|
|
| (13.4.8) |
Преобразование Фурье импульсной функции h (t-t) последнего слагаемого в (13.4.3) с учетом замены переменных (13.4.4) примет вид
| (13.4.9) |
Таким образом, преобразование Фурье левой части равенства (13.4.1) с учетом (13.4.7), (13.4.8) и (13.4.9) примет вид
| (13.4.10) |
или с учетом нижеприведенных обозначений запишется так:
| (13.4.11) |
Здесь
|
| (13.4.12) |
| (13.4.13) |
Отметим, что 
в (13.4.13) является преобразованием Фурье импульсной функции h (x).
Теперь подставим преобразования Фурье левой (13.4.11) и правой (13.4.2) частей в равенство (13.4.1)
 .
| (13.4.14) |
Отсюда следует, что преобразование Фурье импульсной функции h (x) равно
| (13.4.15) |
Из сравнения выражения для передаточной функции H (w) (13.3.5) и равенства (13.4.15) следует, что 
и преобразование Фурье импульсной функции h (x) равно передаточной функции
| (13.4.16) |
Необходимо отметить, что импульсная функция h (x) может быть получена путем применения обратного преобразования Фурье к передаточной функции H (w) (13.3.5)
| (13.4.17) |
Проиллюстрируем это на примере одностепенного осциллятора.
Передаточную функцию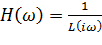 
представим в виде простых дробей
| (13.4.18) |
Здесь w1 и w2 корни выражения L (i w) (13.4.12)
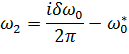
| (13.4.19) |
Подставим (13.4.18) в (13.4.17)
| (13.4.20) |
Интеграл, входящий в (13.4.20), берется с использованием теории вычетов.
Напомним, что если некоторая функция комплексного переменного f (z) регулярна (аналитическая) в области, ограниченной контуром С, кроме конечного числа полюсов в точках а 1, а 1, ¼, аn, то интеграл по контуру С равен сумме всех вычетов в указанных полюсах, умноженной на 2p i
|
|
| (13.4.21) |
Если при этом в окрестности каждой точки 
представима в виде
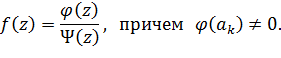
| (13.4.22) |
а 
имеет нуль первого порядка в точках (простые полюса), то есть
то для определения вычетов в таких полюсах существует простая формула
| (13.4.23) |
Поэтому вычет в точках 
или 
функции 
будет иметь вид
| (13.4.24) |
так как 
.
В качестве контура интегрирования С задается действительная ось, на которой как на диаметре строится в верхней полуплоскости полуокружность большого радиуса R (рисунок 1).
| R |
| -R |
| контур С |
| w2 |
| w1 |
Рисунок 1
При устремлении радиуса полуокружности R®∞ интеграл по верхней полуокружности стремится к нулю, в соответствии с леммой Жордана [6]
В область, указанную на рисунке 1, попадают два простых полюса w1 и w2. Следовательно, интеграл, входящий в (13.4.20), будет вычисляться так:
| (13.4.25) |
или по правилу определения вычетов в простых полюсах
| (13.4.26) |
После подстановки в (13.4.26) значений корней w1 и w2 из (13.4.19) интеграл J (x) в (13.4.26) примет вид:
| (13.4.27) |
После подстановки значения интеграла J (x) из (13.4.27) в (13.4.20) получаем следующее выражение для импульсной функции h (x)
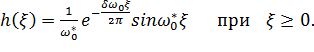
| (13.4.28) |
Сравнение выражений (13.4.28) при 
и (13.2.5) показывает, что путем применения обратного преобразования Фурье к передаточной функции H (w) (см. формулу (13.4.17)) была получена импульсная функция 
.