Определим спектральную плотность и корреляционную функцию выходного процесса y (t) для линейного осциллятора через спектральную плотность и корреляционную функцию входного центрированного случайного процесса х (t). Перепишем для удобства уравнение (13.2.1) для одностепенного осциллятора
 
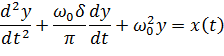
| (13.6.1) |
Корреляционная функция выходного процесса y (t) по определению имеет вид
или с использованием интеграла Дюамеля для  будем иметь
| (13.6.2) |
Запишем выражение для спектральной плотности Sy (w) выходного процесса y, как преобразование Фурье корреляционной функции Ky (t) (13.6.2)
| (13.6.3) |
Введем два сомножителя в (13.6.3), произведение которых равно 1,
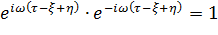
| (13.6.4) |
(13.6.5)
|
Проведем замену переменных t=t – x+h Þ t =t+ x – h и, соответственно, dt=dt.
Тогда (13.6.5) преобразуется к следующему виду
| (13.6.6) |
В (13.6.6) входят передаточная функция H (w) и сопряженная с ней функция H* (w).
| (13.6.7) |
Окончательно связь между спектральными плотностями выходного Sy (w) и входного Sх (w) процессов для одностепенного осциллятора запишется так
| (13.6.8) |
Отметим, что корреляционную функцию Ky (t) можно получить путем применения обратного преобразования Фурье к спектральной плотности Sy (w)
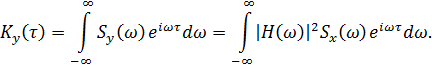
| (13.6.9) |
Известно, что 
связана с дисперсией 
и среднеквадратичным значением 
простым соотношением
| (13.6.10) |
Тогда с учетом (13.6.9) и (13.6.10) среднеквадратичное значение выходной величины будет связано со спектральной плотностью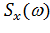 
входной величины 
следующим равенством
| (13.6.11) |
Типовой задачей для осциллятора является следующая задача.
Задан осциллятор с массой m, жесткостью k и логарифмическим декрементом d. На массу осциллятора действует внешняя случайная сила 
со спектральной плотностью 
. Определить среднеквадратичное усилие в пружине осциллятора (собственная частота осциллятора 
)
|
|
Правая часть уравнений (13.6.1) будет выглядеть так
| (13.6.12) |
усилие в пружине осциллятора
| (13.6.13) |
Если в уравнение (13.6.1) подставить значение 
из (13.6.13), а в правую часть 
из (13.6.12), тогда уравнение для усилия в пружине N приобретет вид
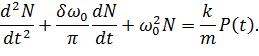
| (13.6.14) |
Структура уравнения для усилия в пружине (13.6.14) очевидно аналогична структуре уравнений (13.6.1) для перемещения 
. При соотношении между правыми частями уравнений (13.6.1) и (13.6.14)
| (13.6.15) |
спектральная плотность 
будет связана со спектральной плотностью 
равенством
| (13.6.16) |
Передаточная функция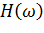 
будет иметь вид (13.3.5).
Поэтому далее для определения среднеквадратичного значения усилия в пружине 
будем пользоваться формулами (13.6.11) и (13.6.16).
| (13.6.16а) |
Остановимся на оценке дисперсии 
(13.6.10) в случае постоянной спектральной плотности входного воздействия 
с использованием теории вычетов.
С учетом представления для передаточных функций в виде простых дробей (13.4.18) выражение для дисперсии выходной величины (13.6.10) запишется так
| (13.6.17) |
Комплексно сопряженная величина передаточной функции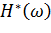 
в (13.6.17) используется без разложения на простые дроби, так как у нее нет полюсов в верхней полуплоскости.
Интеграл в (13.6.17) будем также вычислять путем интегрирования по контуру С, расположенному в верхней полуплоскости (см. рисунок 1), с использованием теории вычетов.
При ограниченной спектральной плотности Sx (w) интеграл по верхней полуокружности равен нулю, так как модуль подынтегральной функции z (w) на полуокружности большого радиуса R мажорируется выражением
|
|
| (13.6.18) |
В области, ограниченной контуром С, имеется два простых полюса w 1 и w 2. Поэтому с использованием теории вычетов для интеграла (13.6.17) получим следующее значение
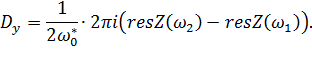
| (13.6.19) |
На основе формулы для вычетов в простых полюсах (13.4.23) в случае белого шума при постоянной плотности 
будем иметь
| (13.6.20) |
После выполнения алгебраических выкладок в скобках формулы (13.6.20) с учетом значений для 
и 
из (13.4.19) получим следующее выражение для дисперсии при постоянном значении спектральной плотности входного воздействия
| (13.6.21) |
С учетом связи между обобщенной спектральной плотностью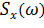 
и спектральной плотностью внешней случайной силы (13.6.16) получаем окончательное выражение для дисперсии усилия в пружине осциллятора в зависимости от постоянной спектральной плотности внешней силы 
| (13.6.22) |
Отметим, что в случае плавно меняющейся спектральной плотности 
в окрестности резонансной частоты w 0 формула (13.6.22) позволяет получить приближенную оценку дисперсии. При этом в формуле (13.6.22) постоянная спектральная плотность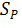 
заменяется на спектральную плотность 
.