Рассмотрим решение задачи об определении внутренних силовых факторов в линейной механической системе при случайном внешнем воздействии.
Пусть конструкция, занимающая область 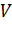 , подвержена системе случайных силовых воздействий или внешних давлений, заданных в некоторых подобластях конструкции
, подвержена системе случайных силовых воздействий или внешних давлений, заданных в некоторых подобластях конструкции 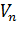 (n = 1, 2,..., N) в виде произведения случайных функций времени
(n = 1, 2,..., N) в виде произведения случайных функций времени  и детерминированных функций координат
и детерминированных функций координат 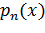
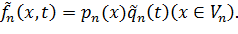
| (13.7.1) |
Конструкция может, например, представлять собой оболочку, на отдельных участках которой (подобластях 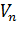 ) заданы случайные акустические воздействия (13.7.1). Требуется определить среднеквадратичные значения виброускорений или напряжений в элементах конструкции.
) заданы случайные акустические воздействия (13.7.1). Требуется определить среднеквадратичные значения виброускорений или напряжений в элементах конструкции.
Запишем уравнение движения конструкции и граничные условия в общей форме
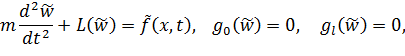
| (13.7.2) |
здесь m – погонная масса или матрица масс;
w – перемещения или кинематический подвектор системы;
L – в общем случае матрица жесткости или дифференциальный оператор, характеризующий упругие свойства системы;
 - граничные условия, записанные в обобщенном виде.
- граничные условия, записанные в обобщенном виде.
Правая часть  – случайная функция имеет следующий вид:
– случайная функция имеет следующий вид:
 . .
| (13.7.3) |
Предварительно с учетом стационарности случайных временных функций  определяются их математические ожидания, которые для стационарных процессов являются константами
определяются их математические ожидания, которые для стационарных процессов являются константами  . В случае если математические ожидания внешних сил
. В случае если математические ожидания внешних сил 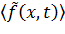 статически уравновешены, математические ожидания всех кинематических и силовых факторов в конструкции определяются путем решения статической задачи
статически уравновешены, математические ожидания всех кинематических и силовых факторов в конструкции определяются путем решения статической задачи
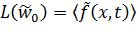
| (13.7.4) |
(в уравнении (13.7.2) отброшены инерционные члены).
Правая часть уравнения (13.7.4) получается из правой части общей задачи (13.7.3) путем замены случайных функций  их математическими ожиданиями
их математическими ожиданиями  .
.
В случае, если математическое ожидание внешних сил 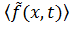 статически неуравновешены, в правую часть уравнения (13.7.4) добавляются инерционные силы от движения изделия как твердого целого. После чего в связанной системе координат решается статическая задача от взаимно уравновешенных внешних и инерционных сил.
статически неуравновешены, в правую часть уравнения (13.7.4) добавляются инерционные силы от движения изделия как твердого целого. После чего в связанной системе координат решается статическая задача от взаимно уравновешенных внешних и инерционных сил.
После определения нагрузок в конструкции от внешних сил, представляющих собой математическое ожидание правой части уравнения (13.7.2) 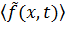 , случайные функции характеризующие изменение внешних сил во времени в (13.7.3)
, случайные функции характеризующие изменение внешних сил во времени в (13.7.3) 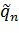 (t), центрируются
(t), центрируются
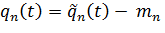
| (13.7.5) |
Затем правая и левая части уравнения (13.7.2) центрируются
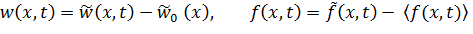
| (13.7.6) |
и с использованием аппарата спектрально-коррекционных представлений решается задача о нагрузках при случайных воздействиях. При этом в уравнении (13.7.2) функция 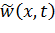 и правая часть
и правая часть  заменяются на центрированные функции
заменяются на центрированные функции 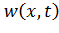 и
и 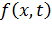 (13.7.6).
(13.7.6).
Отыскивая решение задачи (13.7.2) относительно центрированной функции 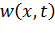
 в виде разложения по собственным формам колебаний
в виде разложения по собственным формам колебаний 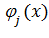
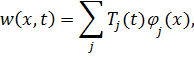
| (13.7.7) |
получим следующие уравнения для обобщенных координат Tj:
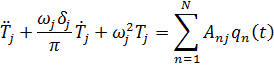
| (13.7.8) |
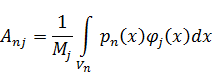
| (13.7.9) |
Здесь 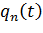 – центрированные случайные функции, характеризующие изменение внешних сил или давлений в каждой подобласти Vn.
– центрированные случайные функции, характеризующие изменение внешних сил или давлений в каждой подобласти Vn.
Решение уравнения (13.7.8)с использованием интеграла Дюамеля (13.2.5) следующим образом выразится через импульсную функцию 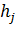 (t) уравнения (13.7.8)
(t) уравнения (13.7.8)
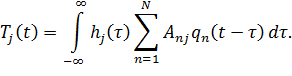
| (13.7.10) |
Любая силовая или кинематическая компонента конструкции x (x,t) на основе метода разложения решения по тонам колебаний представится в виде
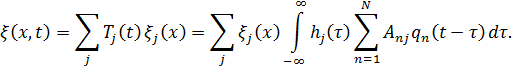
| (13.7.11) |
Здесь  – силовая или кинематическая компонента j -то тона колебаний конструкции.
– силовая или кинематическая компонента j -то тона колебаний конструкции.
Выражение для корреляционных функций выходного процесса Kx (x,t) по параметру x (x,t) запишется так (на основе операции осреднения  )
)
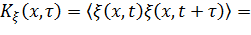
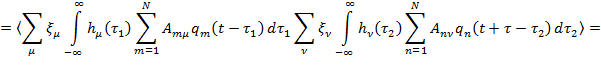
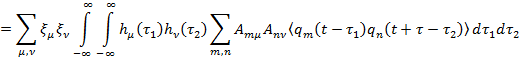
|
| (13.7.12) |
В равенство (13.7.12) входят взаимные корреляционные функции входных силовых воздействий qm(t)

| (13.7.13) |
Таким образом, корреляционная функция выходного процесса  свяжется с корреляционными функциями входных силовых воздействий
свяжется с корреляционными функциями входных силовых воздействий 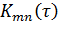 следующим образом
следующим образом

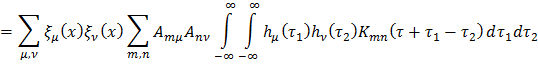
| (13.7.14) |
После определения корреляционных функций выходных параметров  переходим к построению спектральных плотностей с использованием преобразования Фурье
переходим к построению спектральных плотностей с использованием преобразования Фурье

| (13.7.15) |
Подставив в (13.7.15) выражение для корреляционной функции (13.7.14), придем к следующему равенству



|
| (13.7.16) |
(В формулах (13.7.12), (13.7.14), (13.6.16) формы колебаний соответствующего силового или кинематического фактора 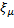 и
и 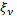 являются функциями координат.)
являются функциями координат.)
В (13.7.16) также как и при получении спектральной плотности одностепенного осциллятора введены два сомножителя типа (13.6.4), произведение которых равно единице.
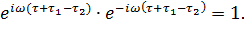
|
Нетрудно видеть, что первые два интеграла, входящие в (13.7.16), являются передаточными функциями уравнений для обобщенных координат (13.7.8) m-го и n-го тонов колебаний (звездочкой * обозначено комплексное сопряжение)


| (13.7.17) |
Введем замену переменных в последнем интеграле, входящем в (13.7.16),
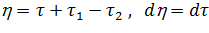 .
.
В итоге получим соотношения для взаимных спектральных 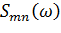 входных случайных силовых воздействий qn (t)
входных случайных силовых воздействий qn (t)
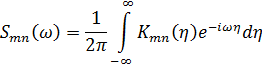
| (13.7.18) |
и спектральную плотность для любой силовой или кинематической компоненты конструкции 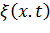
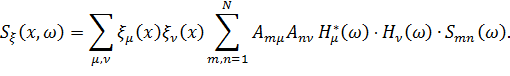
| (13.7.19) |
В связи с тем, что левая часть уравнения (13.7.8) для обобщенных координат совпадает по структуре с уравнением для одностепенного осциллятора, передаточные функции, входящие в (13.7.19) примут вид
 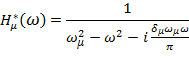
| (13.7.20) |
Проанализируем структуру формулы (13.7.19). Для этого построим передаточные функции системы отдельно для каждого варианта случайного воздействия 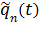 , то есть для каждого варианта внешнего давления, заданного в подобластях конструкции
, то есть для каждого варианта внешнего давления, заданного в подобластях конструкции 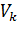 (13.7.3).
(13.7.3).
Это означает необходимость решения уравнения (13.7.2) с правыми частями
 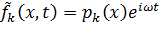 k= 1, 2, ¼, N k= 1, 2, ¼, N
| (13.7.21) |
Будем строить решение для передаточных функций также в виде разложения по тонам колебаний (13.7.7).
Тогда уравнения (13.7.8) для обобщенных координат трансформируются следующим образом:

| (13.7.22) |
Коэффициенты Akj будут иметь структуру, аналогичную (13.7.9).
Решение уравнения (13.7.22) имеет вид

| (13.7.23) |
Таким образом, передаточная функция любой силовой или кинематической компоненты 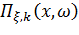 от гармонического воздействия в k -ой области Vk будет иметь вид
от гармонического воздействия в k -ой области Vk будет иметь вид
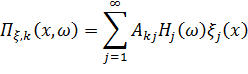
| (13.7.24) |
 k= 1, 2, ¼, N. k= 1, 2, ¼, N.
|
теперь перепишем равенство (13.7.19) в следующей форме
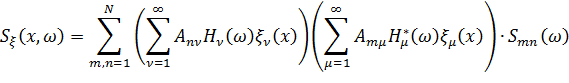
| (13.7.25) |
С учетом формулы для передаточных функций (13.7.24) спектральная плотность любого силового или кинематического параметра 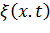 будет связана с матрицей спектральных плотностей
будет связана с матрицей спектральных плотностей 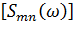 входных случайных воздействий (акустических давлений) следующим равенством
входных случайных воздействий (акустических давлений) следующим равенством

| (13.7.26) |
Отметим, что спектральные плотности выходных параметров в программном комплексе MSC.NASTRAN определяются по формуле, имеющей структуру (13.7.26). При этом передаточные функции 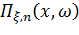 могут определяться как с использованием модального анализа (как это проиллюстрировано в данном разделе), так и прямым методом, с использованием алгебры комплексных чисел (комплексных жесткостей).
могут определяться как с использованием модального анализа (как это проиллюстрировано в данном разделе), так и прямым методом, с использованием алгебры комплексных чисел (комплексных жесткостей).
Дисперсия 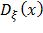 и, соответственно, среднеквадратичное значение
и, соответственно, среднеквадратичное значение  любого силового и кинематического параметра
любого силового и кинематического параметра 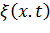 вычисляются по следующей формуле
вычисляются по следующей формуле
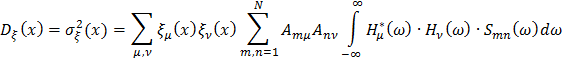
| (13.7.27) |
если внешние случайные воздействия qn, заданные в различных подобластях конструкции (13.7.3), нескоррелированы, внедиагональные элементы матрицы взаимных спектральных плотностей 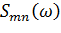 равны нулю. В этом случае формула (13.7.27) преобразуется к следующему виду:
равны нулю. В этом случае формула (13.7.27) преобразуется к следующему виду:
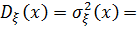
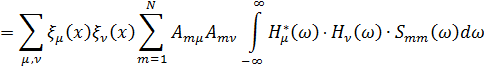
| (13.7.28) |
После нахождения математического ожидания  и среднеквадратичного значения
и среднеквадратичного значения 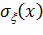 некоторого силового или кинематического фактора
некоторого силового или кинематического фактора 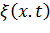 определяется его эксплуатационное значение, соответствующее заданному уровню вероятности непревышения. Так, в предположении нормального закона распределения эксплуатационное значение,
определяется его эксплуатационное значение, соответствующее заданному уровню вероятности непревышения. Так, в предположении нормального закона распределения эксплуатационное значение, 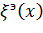 будет иметь вид
будет иметь вид
 ,
,
где k – число квантилей, отвечающее заданному уровню вероятности непревышения Р 0.
Таким образом определяются основные статистические характеристики кинематических и силовых компонент вектора состояния в сечениях конструкции через характеристики стационарного случайного внешнего силового воздействия.