Классы.
1) Сумма двух двузначных чисел равна 147. Оба числа записали в обратном порядке и сложили. Какая сумма могла получиться? Приведите все возможные ответы.
Ответ:84,183.
Решение: Если при сложении не происходило переноса единицы в следующий разряд, то сумма десятков исходных чисел равна 14, а единиц — 7.Значит, получится число 7 •10 + 14 = 84. Если же перенос был, то сумма единиц равна 17,десятков-13,и получится сумма 17•10+13=183.
2) Вдоль забора растут 8 кустов малины, Число ягод на соседних кустах отличается на 1. Может ли на всех кустах вместе быть 225 ягод?
Ответ: не может.
Решение. Число ягод на двух соседних кустах отличается на 1, поэтому на двух соседних кустах вместе нечетное число ягод. Тогда количество ягод на восьми кустах равно сумме четырех нечетных чисел, т. е. числу четному. Значит, значит на всех кустах вместе не может быть 225 ягод.
3)На диагонали ВD квадрата ABCD взяты точки E и F так, что прямая AE пересекает сторону BC в точке М, прямая AF пересекает сторону CD в точке N и CM=CN.Найдите длину диагонали квадрата, если BE=3, EF=4. 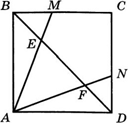
Решение: Из условия следует равенство треугольников АВМ и ADN (ВМ = DN, АВ = АD,угол АВМ равен углу ADN), откуда угол BAE равен углу DAF. Кроме того, АВ = АD и угол АВЕ равен углу ADF. Поэтому треугольники АВЕ и ADF равны, и, значит, DF = ВЕ = 3.
4)Разрежьте фигуру, получаемую из квадрата 7 х 7 вырезанием четырех угловых клеток 1 х 1 (рис. 1), на уголки вида  (уголки состоят из квадратиков размера 1×1)так, чтобы квадратики, отмеченные на рисунке точками, оказались только в больших уголках.
(уголки состоят из квадратиков размера 1×1)так, чтобы квадратики, отмеченные на рисунке точками, оказались только в больших уголках.
Рис 1.  Рис 2.
Рис 2.
Решение: Пример разрезания приведен на рисунке 2.
Классы.
1)Докажите, что  ×
×  ×…×
×…×  <
<  .
.
Решение: Заметим, что  <
<  ,
,  <
<  ,, …,
,, …,  <
<  .Поэтому квадрат рассматриваемого произведения меньше
.Поэтому квадрат рассматриваемого произведения меньше  ×
×  ×…×
×…×  ×
×  =
= 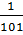 .Значит само произведение меньше
.Значит само произведение меньше  <
<  .
.
2) В некоторой компании 100 акционеров, и любые 66 из них владеют не менее, чем 50 % акций компании. Каким наибольшим процентом всех акций может владеть один акционер?
Ответ:25%
Решение: Решение. Пусть М — акционер, владеющий наибольшим процентом х акций. Разобьем остальных 99 акционеров на три группы А, В и С по 33 акционера. Пусть они владеют соответственно а, b и с процентами акций. Тогда 100-х = а + b + с. Откуда 2 (100-х) = 2 (а + b + с) = (а + b) + (b + с) + (с + а) ≥50 + 50 + 50,т. е. х≤25.Если каждый из 99 акционеров, кроме M, владеет 75/99=25/33% акций, то любые 66 из них владеют ровно 50%, а у М ровно 25% акций.
3) В окружность вписан прямоугольный треугольник АВС с гипотенузой АВ. На большем катете ВС взята точка D так, что АС = ВD, а точка Е — середина дуги АВ, содержащей точку С. Найдите угол DEC.
Ответ:90°.
Решение: Точка Е — середина дуги АВ (рис. 3), поэтому АЕ = ВЕ. Кроме того, вписанные углы САЕ и ЕВС, опирающиеся на одну дугу, равны. Также по условию АС = ВD. Значит, треугольники АСЕ и ВDЕ равны, откуда угол CEA равен углу BED.Но тогда угол DEC равен углу BEA и они равны 90°,т.к. угол BEA равен углу BCA.
| B |
 Рис 3.
Рис 3.
4)На столе донышками вниз стоит 1001 пустой стакан.2 игрока по очереди переворачивают стаканы, в том числе и перевернутые ранее, по следующим правилам:за первый ход можно перевернуть не более 1 стакана, за 2-ой ─не более двух и т.д. При этом за каждый ход необходимо перевернуть хотя бы 1 стакан. Выигрывает тот,после хода которого все стаканы расположены донышками вверх.Кто может выиграть в этой игре независимо от ходов соперника.
Ответ: выигрывает второй игрок.
Решение: Опишем стратегию второго игрока. Пусть второй игрок переворачивает обратно те стаканы, которые перевернул первый, до тех пор, пока первый не сделает свой 500-й ход. Тогда перед ходом первого игрока каждый раз все 1001 стакан стоят донышками вниз. И первый игрок имеет право перевернуть каждым своим ходом не более 999 стаканов (ровно 999 ему можно будет перевернуть только при своем 500-м ходе). Тогда пусть первый игрок при своем 500-м ходе перевернул несколько (не более 999) стаканов. Остались неперевернутыми не более 1000 стаканов. А так как второму игроку своим ходом можно перевернуть1000 стаканов или меньше, то он просто переворачивает оставшиеся стаканы и выигрывает.
Классы.
1)Пусть А — множество таких натуральных чисел, которые записываются только с помощью цифр 1, 5 и 9, причем каждая цифра используется не менее одного раза. Может ли сумма 1001 различного числа из множества А быть полным квадратом?
Ответ: не может.
Решение: Заметим, что числа 1,5,9 имеют вид: 4k+1.Тогда каждое число из A представимо в виде 100a+(4b+1)10+(4c+1)=4m+3(например,1959=19×100+5×10+9).То есть каждое число из A имеет остаток 3 при делении на 4.Тогда и сумма 1001 числа из А также будет иметь остаток 3 при делении на 4,так как 1001=4×250+1.Однако квадраты чётных чисел делятся на 4,а квадраты нечетных чисел имеют остаток 1 при делении на 4,так как (2t+1)2 =4(t2+t)+1.Поэтому сумма 1001 различного числа из A не может быть полным квадратом.
2) Известно, что для некоторых х, у, z выполняется sin у =z  и
и  =z2
=z2  . Докажите, что
. Докажите, что  =z4
=z4  .
.
Решение: Если z=0,то sin y=0,y=πn и все равенства выполнены при любых х. Если  =0,то
=0,то 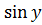 =0,
=0,  =
=  =
=  =
=  =0 и при любом z все равенства выполнены. Если z≠0,sin x≠0, то получаем
=0 и при любом z все равенства выполнены. Если z≠0,sin x≠0, то получаем  =z
=z  , откуда 1=
, откуда 1= 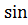 2
2 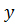 +
+  2
2 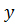 =z2(
=z2(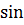 2
2  +
+ 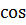 2
2  ),т.е. z2 =1= z4.Тогда
),т.е. z2 =1= z4.Тогда  =
= 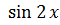 ,sin у =
,sin у =  ,следовательно,
,следовательно,  =1-2
=1-2 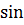 2
2 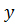 =
=  ,следовательно,
,следовательно,  =sin 4x= z4
=sin 4x= z4  .
.
3) Дан выпуклый четырехугольник ABCD. Известно, что радиусы окружностей, вписанных в треугольники АВС, BCD, CDA и DAB, равны. Докажите, что АС = BD.
Решение: Пусть r-радиусы указанных в условии окружностей. Тогда (рис.4)
SABCD= SABC+ SCDA=  r× (AB+BC+CA) +
r× (AB+BC+CA) +  r× (CD+DA+AC) =
r× (CD+DA+AC) =  r× P+r×AC, где SABCD и Р-площадь и периметр 4-угольника ABCD. Аналогично SABCD= SBCD+ SDAB=
r× P+r×AC, где SABCD и Р-площадь и периметр 4-угольника ABCD. Аналогично SABCD= SBCD+ SDAB=  r× P+r×BD,откуда следует AC=BD.
r× P+r×BD,откуда следует AC=BD.
| B |
| D |
 Рис 4.
Рис 4.
4) Все боковые грани четырехугольной пирамиды — прямоугольные треугольники с вершиной прямого угла на основании пирамиды. Может ли основание высоты пирамиды быть внутренней точкой ее основания?
Ответ: нет, не может.
Решение: Пусть SABCD — данная пирамида (рис. 5). Предположим, что вершины прямых углов боковых граней пирамиды являются четырьмя различными точками. Без ограничения общности можно считать, что углы SAB,SВС,SCD,SDA равны между собой и равны  .Тогда SB > SA,
.Тогда SB > SA,
SC > SB, SD > SC и SA > SD. Отсюда SA > SA — противоречие. Значит, хотя бы одна из вершин основания пирамиды является вершиной прямого угла для двух боковых граней. Пусть, например, это вершина А, тогда ребро SA перпендикулярно двум пересекающимся прямым АВ и АD основания пирамиды, следовательно, SA — высота пирамиды.
| D |
 Рис 5.
Рис 5.
Заключение.
Подводя итог, я рассмотрел все компоненты связанные с математической олимпиадой и пришёл к выводу, что математические олимпиады имеют огромное значение для учащихся школ.
Иногда может случится так, что сильное увлечение математикой начинается с решения какой-либо задачи,не похожей на другие. Такая задача может встретиться на занятии в школе, на математическом кружке, в журнале или книге. Хорошим источником таких задач служат различные олимпиады – от школьных, районных и городских до международных. Решение олимпиадных задач обычно не требует знаний, выходящих за рамки школьной программы. Такие задачи, как правило сформулированы так, что они не принадлежат ни к одному из обычных типов задач школьного математического курса. Поэтому решение каждой такой задачи требует особого подхода, внимания, наличие способности к творческому труду. Умение решать нестандартные задачи свидетельствует о глубоком владение математическим аппаратом и развитой культуре математического мышления, а владение предметом гораздо важнее, чем просто «чистые знания», которые всегда можно пополнить с помощью хороших справочников.
Математические олимпиады помогают распространить знания среди учащейся молодёжи и играют большую роль в повышении уровня преподавания математики в средней школе. Благодаря проведению математических олимпиад повышается интерес учащихся к математике; активизируются все форы внеклассной и внешкольной работы; они оказывают помощь выпускникам в выборе будущей профессии.
Список использованной литературы.
1) https://www.scienceforum.ru
2) https://ru.wikipedia.org
3) Агаханов Н.Х., И.И.Богданов, П.А.Кожевников: “Математика. Всероссийские олимпиады “(вып.1),2008г.
4) Агаханов Н.Х., О.К.Подлипский: “Математика. Всероссийские олимпиады “(вып.2),2009г.
5) https://rmomatematik.jimdo.com.