КУРСОВАЯ РАБОТА
Выполнила:
студентка 3 курса очной формы обучения
Шадрина Ирина Викторовна
Руководитель:
дфмн, проф. Хэкало С.П.
Итоговая оценка - ______________
Подпись______________________
Коломна – 2017 г.
Содержание
Интеграл эйлер бета гамма
Введение........................................................ 3
1.Интеграл Эйлера первого рода (бета-функция Эйлера)................ 4
2. Интеграл Эйлера второго рода (гамма-функция Эйлера).............. 7
Определение Эйлерова интеграла второго рода....................7
Свойства гамма-функции Эйлера............................... 8
Непрерывность гамма-функции Эйлера.......................8
Основное функциональное уравнение........................ 9
Поведение гамма-функции и её график....................... 10
Связь между бета- и гамма-функциями....................... 13
Формула дополнения...................................... 15
Формула Эйлера.......................................... 15
Примеры вычисления интегралов с использованием эйлеровых
Интегралов....................................................... 18
Заключение...................................................... 19
Список литературы................................................ 20
Введение.
Во многих случаях невозможно выразить первообразную от заданной элементарной функции никакими конечными комбинациями основных элементарных функций. О таких функциях говорят, что они не интегрируемы в конечном виде. В некоторых случаях, для вычисления используют так называемые эйлеровы интегралы, которые являются особым классом функций, они представляются в виде собственного либо несобственного интеграла, который зависит не только от формальной переменной, но и от параметра. К эйлеровым интегралам относятся так называемые бета- и гамма-функции Эйлера.
Гамма-функция относится к числу самых простых и значимых специальных функций, применение её свойств поможет при изучении многих других специальных функций, например, цилиндрических, гипергеометрических и других.
Благодаря её введению значительно расширяются возможности при вычислении интегралов. Даже в случаях, когда конечная формула не содержит никаких функций, кроме элементарных, получение её всё же часто облегчает использование гамма-функции, хотя бы при промежуточных преобразованиях.
Эйлеровы интегралы являются хорошо изученными неэлементарными функциями. Задача считается решённой, когда она приводится к вычислению эйлеровых интегралов.
Цель данной работы заключается в следующем: изучить бета- и гамма-функции, их свойства, установить связь между ними и научиться применять их для вычисления интегралов.
1.Интеграл Эйлера первого рода (бета-функция Эйлера).
Бета – функцией или интегралом Эйлера первого рода называют интеграл:
Данный интеграл представляет собой функцию от двух переменных параметров a и b. Когда эти параметры удовлетворяют условиям 
>1, 
<1, то интеграл (1.1) будет несобственным интегралом, зависящим от параметров и 
,причём особыми точками этого интеграла будут точки 
и 
.
Данный интеграл (1.1) сходятся при 
.Полагая 
получим:
т.е. данная функция симметрична относительно параметров и .
Учитывая, что
используя формулу интегрирования по частям и выполняя тождественные преобразования получим:
Откуда
При целом = n последовательно применяя (1.2) получим:
при целых = m, = n, имеем
но B(1,1) = 1,поэтому:
Считаем, что в (1.1) 
. Так как график функции 
симметричен относительно прямой 
,то
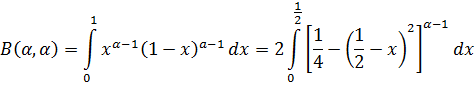
и после подстановки 
, имеем:
Заменяя в (1.1) 
, откуда получим
Бета-функция очень просто выражается через другую функцию, которую мы рассмотрим в следующем разделе.
2. Интеграл Эйлера второго рода (гамма-функция Эйлера)
2.1 Определение Эйлерова интеграла второго рода
Название гамма-функция Эйлера данному интегралу дал Лежандр:
Этот интеграл сходится при любом 
> 0, так как особые точки ¥ и 0 (при 
< 0). 
существует лишь при > 0 (бесконечно малая порядка 
– 1 по отношению к 
).
существует, каково бы ни было а, так как, взяв 
> 1, имеем:
Значит, 
существует при > 0.
Интеграл 
определяет гамма-функцию.
Гамма-функция, наравне с элементарными, является одной из важнейших функций для математического анализа и его приложений. Глубокое изучение свойств гамма-функции, исходя из ее интегрального определения (2.1), служит примером применения теории интегралов, зависящих от параметра. Положим в формуле (2.1) 
найдем:
Как известно, 
, причем выражение 
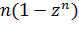при возрастании n стремится к своему пределу, возрастая. В таком случае, на основании предельного перехода под знаком интеграла, оправдано равенство: Г () = 
.
Если сделать подстановку z = yn, получим:
Но, согласно формуле (1.3):
Итак, мы пришли к знаменитой формуле Эйлера-Гаусса:
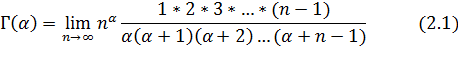
Cвойства гамма-функции будут получены из ее интегрального представления (2.1).
2.2 Свойства гамма-функции Эйлера
Непрерывность гамма-функции Эйлера
Функция Г () при всех значениях > 0 непрерывна и имеет непрерывные производные всех порядков. Поэтому стоит доказать лишь существование производных. Находя производную интеграла (2.1) под знаком интеграла, получим:
применение правила Лейбница объясняется тем, что оба интеграла
сходятся равномерно относительно : первый при х = 0 для 
> 0 (мажоранта 
), а второй сходится при х = 
для 
А < (мажоранта хА е-х).
Таким же образом можно убедиться и в существовании второй производной
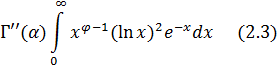
и всех следующих.