Для установления связи между бета- и гамма -функциями, мы сделаем подстановку 
в формуле (2.1) и получим:
Умножим обе части этого равенства на 
, получим:
Заменяя здесь 
на 
и одновременно t на 
, получим:
Умножим обе части этого равенства на 
и проинтегрируем по t от 0 до 
:
=
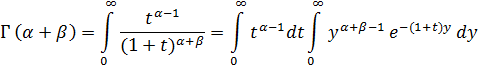
В интеграле слева стоит функция 
справа же переставим интегралы. Получим:
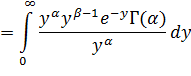
Итак, получаем:
, откуда,
Вывод этого соотношения Эйлера принадлежит Дирихле. Но для его обоснования надо еще оправдать перестановку интегралов. Ограничимся поначалу предположением, что 
> 1, 
> 1. Тогда для функции 
оказываются выполнимыми все условия следствий интегрирования интеграла по параметру.
А именно: эта функция непрерывна и притом положительна для 
, а интегралы
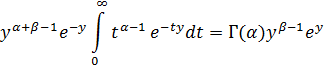
в свою очередь представляют собой непрерывные функции: первый – от t для t 
0, второй – от у для у 0. Ссылка на упомянутое следствие оправдывает перестановку интегралов, а с нею и формулу (2.8) – для 
Если же известно лишь, 
то – по доказанному – имеем
А отсюда, используя формулы (1.2), (1.3) приведения для функции 
и (2.5) для функции Г, легко вновь получить формулу (2.10) уже без ненужных ограничений.
Формула дополнения
Если в формуле (2.10) положить 
, то, используя формулы (1.6) и (2.7), получим соотношение:
Эта формула называется формулой дополнения. При 
находим (так как 
).
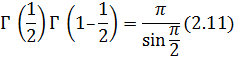
Формула Эйлера
В качестве применения формулы дополнения определим величину произведения (где n – любое натуральное число)
Запишем это произведение в обратном порядке:
перемножим оба выражения:
и к каждой паре множителей применим формулу дополнения. Мы получим:
|
|
Теперь для вычисления произведения синусов рассмотрим тождество:
и устремим в нем 
, получим:
или, приравнивая модули:
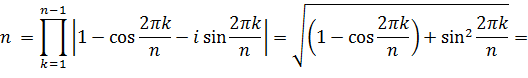
получили
Подставляя это выражение для Е 2, окончательно получаем:
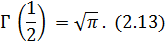
Если в интеграле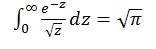 
сделать подстановку 
, то получим значение интеграла Эйлера-Пуассона:
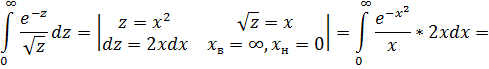
Примеры вычисления интегралов с использованием эйлеровых интегралов.
Вычислить интегралы:
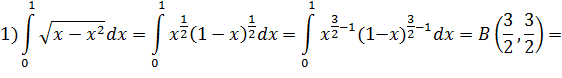
Заключение.
Гамма и бета-функции являются удобным средством для вычисления некоторых интегралов в частности многих из тех интегралов, которые нельзя представить в элементарных функциях.
Для гамма-функции составлены подробные таблицы, и при вычислениях она может использоваться наравне с простейшими элементарными функциями.
Определенные интегралы различных типов могут быть выражены через гамма-функцию. В частности, к таким интегралам нередко приводят задачи, связанные с вычислением площадей и объемов.
Благодаря этому эйлеровы интегралы широко применяются в математике и ее приложениях, в механике, термодинамике и в других отраслях современной науки.
Список литературы.
1. Аксенов А.П. Математический анализ (Определенный интеграл. Несобственные интегралы. Приложения определенного интеграла). – СПб.: Нестор, 1999
2. Бермант А.Ф., Араманович И.Г. Краткий курс математического анализа. – М.: Наука, 1966. – 735 с.
3. Виленкин Н.Я., Куницкая Е.С, Мордкович А.Г., Математический анализ: интегральное исчисление. – М.: Наука, 1979. – 435 с.
|
|
4. Виленкин Н.Я. Специальные функции. – М.: Наука, 1976. – 412 с.
5. Лебедев И.И. Специальные функции и их приложения: М., гостехтериоиздат,1953-234 с.
6. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Т. 1, 2. – М.: Физматгиз, 1962. – 807 с.