Примеры конструктивных теорем

Оглавление

1.Введение……………………………………………………………………………3.

2.Примеры конструктивных теорем.

2.1. Теорема о существовании максимума и минимума на отрезке у дифференцированной функции……………………………………………………...3.

2.2. Условия независимости криволинейного интеграла 2-го рода от пути интегрирования……………………………………………………………………….4.

2.3. Теорема о существовании непрерывной функции всюду не дифференцируемой…………………………………………………………………..5.

2.4. Теорема о существовании четной и нечетной функции одновременно….7.

2.5. Если функция удовлетворяет условию симметрии, то ее можно представить в виде суммы двух функций - четной и нечетной : области определения которых те же, что у функций , причем такое представление единственно…………………………………………………………………………..8.

3. Примеры неконструктивных теорем.

3.1. Теорема Ферма…………………………………………………………………8.

3.2. Теорема Ролля………………………………………………………………….9.

3.3. Теорема Лагранжа……………….....................................................................10.

3.4. Теорема об интегральном среднем…………………………………………..11.

3.5. Теорема о существовании точных верхней и нижней граней у ограниченного множества………………………………………………………….12.

4. Применение теорем для решения задач………………………………………...13.

5. Заключение………………………………………………………………………..14.

6. Литература………………………………………………………………………...15.

 

Введение

Если посмотреть вокруг, то роль математики в жизни человека становится очевидной. Телефоны, компьютеры и прочая электронная техника сопровождают нас каждый день, а их создание было бы невозможно без использования законов и расчетов этой величайшей науки

В данной работе, будет встречаться довольно-таки часто такое понятие как «функция». Оно прошло долгую и довольно-таки сложную эволюцию. Термин «функция» впервые появился в 1692г. у Г. Лейбница, в некотором более узком смысле. В смысле, близком к современному, этот термин употребил в письме к Лейбницу в 1698г. швейцарский учёный И. Бернулли.

В формировании современного понимания функциональной зависимости приняли участие многие крупные математики, такие как: Ферма, Ролль, Лагранж, Вейерштрасс, о теоремах которых я сейчас и расскажу.

В своей курсовой работе буду рассматривать два вида теорем о существовании: конструктивные и неконструктивные.

Первые, конструктивные, в процессе доказательства приводят к построению нужного объекта, то есть предъявляют объект с нужными свойствами явно, например формулой заданную функцию и тому подобное.

Вторые, неконструктивные, доказывают существование, например точки, но не отвечают на вопрос как её найти.

Примеры конструктивных теорем

2.1. Теорема. Если дифференцируемая функция имеет экстремум в точке , то ее производная в этой точке равна нулю, .

Доказательство. Пусть – точка максимума. Следовательно, в окрестности точки выполняется неравенство .

Тогда если и ,

Если . По условию теоремы производная функции

существует. Переходя к пределу при , получим , если и , если . Это возможно лишь в случае .

Аналогично можно показать утверждение теоремы если – точка минимума.

Замечание. Геометрически утверждение теоремы означает, что в точках экстремума касательные к графику функции параллельны оси (рис.65). Обратная теорема не верна. Если , то это не всегда означает, что точка – точка экстремума. Действительно, для функции в точке 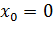производная , , но точка 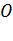не является ни минимумом, ни максимумом (рис.66). Существуют так же функции, которые в точках экстремума не имеют производных. Так функция в точке 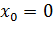не имеет производной, но эта точка является ее минимумом (рис.67).

 

2.2. Условия независимости криволинейного интеграла 2-го рода от пути интегрирования.

Теорема. Пусть - односвязная область в , ограниченная и замкнутая (односвязный компакт) и пусть на заданы функции и -непрерывные на вместе со своими частными производными и , тогда следующие условия равносильны:

1) при любом замкнутом контуре , целиком лежащим в .

2) не зависит от пути, соединяющего две фиксированные точки в .

3) 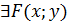, определённая на и дифференцируема на , такая что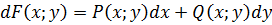

4) 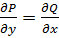– условие Коши-Римана-Даламбера

Докажем равносильный переход от условия 2 к условию 3:

Доказательство.

Пусть не зависит от пути, соединяющего две фиксированные точки в .

Пусть , ; -путь, проведенный из в

Рассмотрим функцию и заметим, что хотя мы выбирали произвольно, в силу условия 2 интеграл не зависит от выбора конкретного пути , а следовательно и функция при условии фиксированной начальной точки зависит только от координат конечной точки

Покажем, что данная функция удовлетворяет условию 3. Для этого рассмотрим частное приращение (по теореме Лагранжа получаем)= , где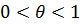

Перейдем к пределам:

Последнее равенство получено из условия, что -непрерывная функция.

Таким образом, данный предел существует и по определению он равен частной производной по

Аналогично

Напомним, что если - дифференцируема, то

В нашем случае, если - дифференцируема, то

Заметим, что правая часть выражения (*) может существовать, но не являться дифференциалом. Однако, можно воспользоваться достаточным условием дифференцируемости, а именно, - дифференцируема, если частная производная непрерывна. Так как и равны и и также равны соответственно, а они по условиям теоремы непрерывны, то следовательно - дифференцируема. Значит выражение (**) является ее дифференциалом. Что и требовалось доказать

 

2.3. Небольшая историческая справка, касательно происхождения данной теоремы:

В 1806 году Ампер предпринял попытку доказать аналитически, что всякая «произвольная» функция дифференцируема всюду, за исключением «исключительных и изолированных» значений аргумента. При этом принималась за очевидное возможность разбиения интервала изменения аргумента на части, в которых функция была бы монотонна. С этими оговорками гипотезу Ампера можно рассматривать как нестрогую формулировку теоремы Лебега. В первой половине XIX века предпринимались попытки доказать гипотезу Ампера для более широкого класса, именно для всех непрерывных функций. В 1861 году Риман привел своим слушателям в качестве контрпримера следующую функцию

{\displaystyle r(x)=\sum \limits _{n=1}^{\infty }{\frac {\sin n^{2}x}{n^{2}}}};

однако исследование дифференцируемости этой функции чрезвычайно сложно. Джозеф Гервер доказал, что эта функция все же имеет производную в некоторых рациональных точках, лишь в 1970 году. В 1872 году Вейерштрасс указал более простой контрпример — введенную выше функцию {\displaystyle w} 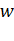и представил строгое доказательство её недифференцируемости. В печати этот пример впервые появился в 1875 году в работе П.Дюбуа-Реймона. Ещё более простой пример принадлежит ван дер Вардену (1930):

{\displaystyle v(x)=\sum \limits _{n=0}^{\infty }{\frac {\{10^{n}x\}}{10^{n}}}} ,

где фигурные скобки означают взятие дробной части.

В качестве доказательства данной теоремы, я приведу в пример функцию, которая обладает свойством непрерывности и всюду не дифференцируема.

Функция Вейерштрасса — пример непрерывной функции, нигде не имеющей производной, как контрпример для гипотезы Ампера.

Функция Вейерштрасса задается на всей числовой прямой единым аналитическим выражением:

{\displaystyle w(x)=\sum _{n=0}^{\infty }b^{n}\cos(a^{n}\pi x)},

где {\displaystyle a} 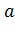— произвольное нечетное число, не равное единице, а {\displaystyle b} — положительное число, меньшее единицы. Этот функциональный ряд мажорируется сходящимся числовым рядом

{\displaystyle \sum _{n=0}^{\infty }b^{n}} ,

поэтому функция {\displaystyle w} определена и непрерывна при всех вещественных {\displaystyle x} . Тем не менее эта функция не имеет производной по крайней мере при

{\displaystyle ab>{\frac {3}{2}}\pi +1} .

Для доказательства отсутствия производной в произвольной точке {\displaystyle x_{0}} , строят две последовательности {\displaystyle \{x_{m}\}} и {\displaystyle \{y_{m}\}} , сходящиеся к точке {\displaystyle x_{0}} , и доказывают, что отношения

{\displaystyle {\frac {w(x_{m})-w(x_{0})}{x_{m}-x_{0}}}} и {\displaystyle {\frac {w(y_{m})-w(x_{0})}{y_{m}-x_{0}}}} имеют разные знаки по крайней мере при

{\displaystyle ab>{\frac {3}{2}}\pi +1} и {\displaystyle a>1} .

Указанные последовательности могут быть определены как

{\displaystyle x_{m}={\frac {\gamma _{m}-1}{a^{m}}}} и {\displaystyle y_{m}={\frac {\gamma _{m}+1}{a^{m}}},} ,

где {\displaystyle \gamma _{m}} — ближайшее целое число к {\displaystyle a^{m}x_{0}.}

Отсутствие производной во всех точках при более общих условиях

{\displaystyle ab\geq 1} и {\displaystyle a>1} было установлено Харди.

Таким образом, я доказал, что существует такая функция, которая непрерывна и всюду не дифференцируема. И название у такой функции, функция Вейерштрасса.

2.4. Теорема о существовании четной и нечетной функции одновременно.

Для начала, хотелось бы привести определения четной или нечетной функции: функция называется четной, если для каждого из области определения функции выполняется равенство ;

функция называется нечетной, если для каждого из области определения функции выполняется равенство .

А также перечислим ряд свойств этих функций:

сумма или разность двух четных (нечетных) функций есть четная (нечетная) функция;

произведение или частное двух одинаковых по четности функций есть четная функция;

произведение или частное двух разных по четности функций есть нечетная функция;

композиция двух функций одинаковой четности есть функция той же четности;

композиция двух функций разной четности есть функция четная;

если внутренняя функция четная, то ее композиция с произвольной внешней функцией есть функция четная.

 

Доказательство. Для произвольной функции , заданной на симметричной относительно нуля области определения, положим:

;

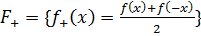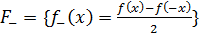
Замечание. В множествах и 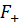включены все четные и нечетные функции.

Нам требуется доказать, что пересечение множеств В самом деле, пусть функция -и четная, и нечетная функция одновременно. Тогда получаем систему ; Вычтем из первого уравнения второе. Получим, что , откуда следует, что для любого . Опираясь на вышеизложенное, можно сделать вывод о том, что тождественно нулевая функция является и четной, и нечетной одновременно и других таких функций нет.Что и требовалось доказать.

2.5. Если функция удовлетворяет условию симметрии, то ее можно представить в виде суммы двух функций - четной и нечетной

: области определения которых те же, что и у функций , причем такое представление единственно.

Доказательство.

При доказательстве теоремы, буду опираться на материал, представленный в пункте 2.4.

Рассмотрим сумму: . Теперь убедимся, что данное разложение единственно. Для этого зададим две функции и , такие что, справедливо равенство . Тогда получим, что (1). Выражение (1) равносильно выражению .

Обозначим , и . Теперь по свойствам четных и нечетных функций будем иметь:

и . Что и требовалось доказать.