Применение теоремы Лагранжа
Пример. Решить уравнение: 
.
Решение. Увидим, что 
и 
являются корнями данного уравнения. Докажем, что других корней уравнение не имеет. Предположим, что уравнение имеет три корня 
. Рассмотрим функцию 
. Данная функция непрерывна на всей прямой и имеет всюду производную. Тогда, по теореме Лагранжа имеет:
,
,
Следовательно, существуют хотя бы две точки 
и 
, в которых производная функции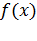 
равна нулю. Однако функция 
имеет только один корень. Этим доказано, что данное уравнение имеет только два корня и .
Ответ: 
, 
.
Применение теоремы Ролля
Задание. Показать, что функция 
удовлетворяет условиям теоремы Ролля на промежутке 
и найти точку 
, в которой 
Функция дифференцируема на промежутке и на его концах принимает одинаковые значения:
Тогда, по теореме Ролля, существует точка , в которой 
.
Найдем производную заданной функции 
. Найдем значение производной в точке 
и приравняем полученное значение к нулю:
следовательно 
Ответ:
Применение теории максимума и минимума функций к решению задач
Какие размеры надо придать цилиндру, чтобы при данном объеме 
его полная поверхность 
была наименьшей?
Решение. Обозначая через 
радиус основания цилиндра и через 
высоту цилиндра, будем иметь 
.
Так как объем цилиндра задан, по при данном величина определяется формулой 
откуда 
Подставляя это выражение 
в формулу для 
, получим 
, или 
.
Здесь - заданное число. Таким образом, мы представили как функцию одной независимой переменной .
Найдем наименьшее значение этой функции в промежутке 
:
При 
Следовательно, в точке функция имеет минимум. Заметив, что 
и 
т. е. что при стремлении к нулю или к бесконечности поверхность неограниченно возрастает, мы приходим к выводу, что в точке функция имеет наименьшее значение.
Но если 
, то 
. Значит для того, чтобы при данном объеме полная поверхность цилиндра была наименьшей, высота цилиндра должна равняться его диаметру
Заключение
Подводя итог изучения темы “Теоремы о существовании”, хотелось бы отметить, что мне понравилась простота и четкость изучаемых теорем. Это безусловно преимущества, которые были выявлены в ходе изучения темы.
Но есть, к сожалению, и недостатки. Не совсем доступны для понимания некоторые теоремы. Например теоремы Ролля, Лагранжа, Ферма. Они требуют каких-то дополнительных знаний, углубленного изучения материала, поиска подходящих примеров.
Даже несмотря на все это, актуальность и значимость вышеизложенных теорем очень велика.
Литература
1)Баврин И.И. Высшая математика: Учеб. Для студ. естественно-научных специальностей педагогических вузов / Иван Иванович Баврин. – 4-e изд., испр. и доп.- М.: Издательский центр «Академия», 2004.-616 с; с. 178-181.
2) Полубаринова-Кочина П.Я. Карл Вейерштрасс. Москва: Наука, 1985.
3) Пискунов Н. С. Дифференциальное и интегральное исчисления для втузов, т.1: Учебное пособие для вузов.— 13-е изд.— М.: Наука. Главная редакция физико-математической литературы, 1985. — 432 с; c. 159-160.
4)Зорин В.А. Математический анализ; М.:ФАЗИС; Наука; Ч.1.-1997, 568с; стр.210-212
5)Кудрявцев Л.Д. Дифференциальное и интегральное исчисления функций одной переменной; М.: Дрофа; т.1.-2003, 704с.
6)Бунимович Е.А. Математика в школе; ООО «Школьная Пресса»; 2002.№6, 1-80; с.63-64.