Рассмотрим несколько свойств однородных функций:
1. Если 
однородная функция с порядком однородности q, то ее дробная производная порядка 
, вычисляемая как 
по и любой независимой переменной начиная от нуля (при условии существования соответствующего интеграла, для чего требуется выбирать 
)- это однородные функции с порядком однородности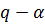 
. Рассмотрим функцию и
. Тогда с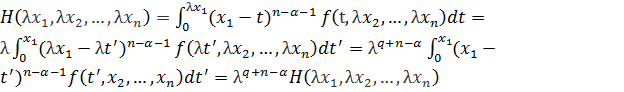 
(здесь сделана замена переменной интегрирования 
После n-кратного дифференцирования по переменной x1 однородная функция 
порядка 
становится однородной функцией с порядком однородности 
.
2. Если однородная функция с порядком однородности q, то ее n-мерная свертка с обобщенным Абелевым ядром, вычисляемая как 
п(при условии существовании соответствующего интеграла)- это однородная функция с порядком однородности 
. В Доказательство. 
, где сделана замена переменных интегрирования 
.
3. Теорема Эйлера для однородныхфункций. Для того, чтобы дифференцируемая функция 
{\displaystyle f(x_{1},x_{2},...,x_{n})} была однородной функцией с порядком однородности {\displaystyle q,}необходимо и достаточно выполнение соотношения Эйлера
.
Доказательство.
Необходимость получается из дифференцирования равенства
при 
. Для доказательства достаточности возьмем функцию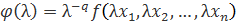 
при фиксированных 
. Продифференцируем ее по 
:
.
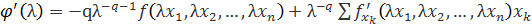В силу условия 
получаем 
и 
. Константу c определяем из условия 
.
В результате, 
.
Метод Эйлера
Метод Эйлера часто называют видоизменённым методом Эйлера или методом собственных чисел и собственных векторов. Он применяется для решения линейных однородных систем дифференциальных уравнений с постоянными коэффициентами. Пусть дана система n линейных однородных дифференциальных уравнений с n неизвестными функциями, коэффициенты которой постоянные:
Эту систему можно записать в виде матричного дифференциального уравнения:
,
где 
, 
, 
.
Решение системы найдём в виде: 
где , 
(i = 1, 2,..., n) — постоянные величины.
Подставив значения 
(i = 1, 2,..., n) в систему дифференциальных уравнений, получим систему линейных алгебраических уравнений относительно :
Так как система имеет ненулевое решение тогда и только тогда, когда определитель основной матрицы равен нулю, то получим следующее уравнение n -й степени:
.
Это уравнение позволит найти . Оно является характеристическим уравнением матрицы А и одновременно характеристическим уравнением системы.
Пусть характеристическое уравнение имеет n различных корней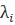 
(i = 1, 2,..., n), которые являются собственными числами матрицы А. Каждому собственному числу соответствует свой собственный вектор.
Пусть характеристическому числу 
соответствует собственный вектор (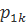
; 
;...; 
), где k = 1, 2,..., n. Тогда система дифференциальных уравнений имеет n решений:
1-е решение, соответствующее корню = 
:
, 
,…, 
;
2-е решение, соответствующее корню = 
:
, 
,…, 
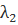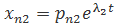и т.д.;
n-е решение, соответствующее корню = 
:
, 
,…, 
.
Таким образом, получили фундаментальную систему решений. Общее решение системы имеет вид:
Пример. Найти общее решение системы дифференциальных уравнений:
Решение. Данная система является линейной однородной системой дифференциальных уравнений второго порядка с постоянными коэффициентами. Решим ее методом Эйлера.
Составим характеристическое уравнение матрицы системы
Его корни = –2; 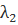= 2 — характеристические числа матрицы.
При = –2 уравнения для определения собственного вектора имеют вид:
=> 
– 
= 0 => р1 = р2 =>
(1; 1) — собственный вектор.
При 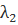= 2 уравнения для определения собственного вектора имеют вид:
=> + = 0 => р1 = -р2 =>
(1; -1) — собственный вектор.
Получаем фундаментальную систему решений:
для = –2: х11 = е-2t, х21 = е-2t ;
для 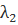= 2: х12 = е2t, х22 = – е2t.
Общее решение системы имеет вид:
