Пример 20.
Доказать, что при любом натуральном n справедливо равенство
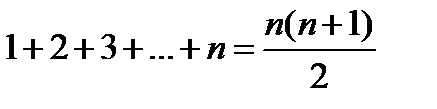

1) Проверим, что это тождество верно при n = 1.

 - верно.
- верно.
2) Пусть тождество верно и для n = k, т.е.

3)Докажем, что это тождество верно и для n = k + 1, т.е.
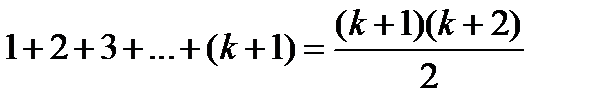


Что и требовалось доказать.
Пример 21.
Доказать формулу 
1)  . Левая часть равна 1. Правая часть
. Левая часть равна 1. Правая часть  . Следовательно, при
. Следовательно, при  верно.
верно.
2) 
3) n=  .
.
Получим: 
 +(k+1)2.
+(k+1)2.
Действительно, 

 =
= 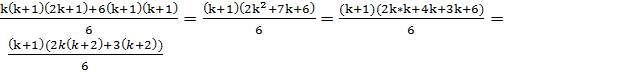 =
=  , что и требовалось доказать.
, что и требовалось доказать.
Пример22.
Доказать, что 13+23+33+43+…+n3=(1+2+3+4+…+n)2.
1) При n=1. 13=12 – верно.
2) При n=k. 13+23+33+43+…+k3=(1+2+3+4+…+k)2 – верно.
3) При n=k+1.
Доказать, что 13+23+33+43+…+k3+(k+1)3=(1+2+3+4+…+k+(k+1))2.
13+23+33+43+…+k3+(k+1)3=(1+2+3+4+…+k+(k+1))2.
Отсюда (1+2+3+4+…+k+(k+1))2 - 13+23+33+43+…+k3=(k+1)3.
Тогда: (1+2+3+4+…+k+(k+1))2 - (1+2+3+4+…+k)2 = ((1+2+3+…+k+(k+1))-(1+2+3+…+k))*((1+2+3+…+k+(k+1))+(1+2+3+…+k)) = (k+1)(2∙(1+2+3+…+k)+(k+1)) = (k+1)(2∙  ∙k+(k+1)) = (k+1)(k(k+1)+(k+1)) = (k+1)(k2+2k+1)=(k+1)(k+1)2=(k+1)3, что и требовалось доказать.
∙k+(k+1)) = (k+1)(k(k+1)+(k+1)) = (k+1)(k2+2k+1)=(k+1)(k+1)2=(k+1)3, что и требовалось доказать.
Пример 23.
Докажите тождество
2  2
2  + 3
+ 3  2
2  + 4
+ 4  2
2  + … + n
+ … + n  2
2  = (n - 1)
= (n - 1)  2
2 
1) Проверим, что это тождество верно при n = 2.
2  2
2  = (2 - 1)
= (2 - 1)  2
2 
4 = 4 – верно
2) Пусть тождество верно для n = k, т.е.
2  2
2  + 3
+ 3  2
2  + 4
+ 4  2
2  + … + k
+ … + k  2
2 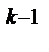 = (k - 1)
= (k - 1)  2
2 
3) Докажем, что это тождество верно и для n = k + 1, т.е.
2  2
2  + 3
+ 3  2
2  + 4
+ 4  2
2  + …+ k
+ …+ k  2
2  + (k + 1)
+ (k + 1)  2
2  = k
= k  2
2 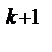
2  2
2  + 3
+ 3  2
2  + 4
+ 4  2
2  + …+ k
+ …+ k  2
2  + (k + 1)
+ (k + 1)  2
2  = (k - 1)
= (k - 1)  2
2  + (k + 1)
+ (k + 1)  2
2  =
=
= (k –1 + k + 1)  2
2  = 2k
= 2k  2 = k
2 = k  2
2 
Пример 24.
Докажите тождество 

 …
… 

При n 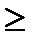 2
2
1) Проверим, что это тождество верно для n = 2
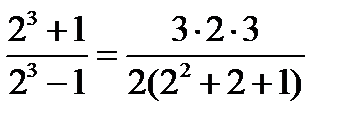
 - верно
- верно
2) Пусть формула верна для n = k, т.е.
 …
… 
3) Докажем, что эта формула верна и для n = k + 1, т.е.
 …
…  =
=  = =
= =  =
= 
Пример 25.
Докажите тождество 
1.Проверим, что это тождество верно при n = 1.

1 – 8= −7
−7=−7 - верно.
2.Пусть тождество верно и для n = k, т.е.
13−23+33−43+ …+(2k−1)3−(2k)3= −k2(4k+3)
3.Докажем, что это тождество верно и для n = k + 1, т.е.
13−23+33−43+ …+(2k−1)3−(2k)3+(2(k+1) −1)3−(2(k+1))3=
=−(k+1)2(4(k+1)+3)= −(k+1)2(4k+7)
М – сумма 2) и 3). 
М =  =
=  =
=
=  =
=
=  =
= 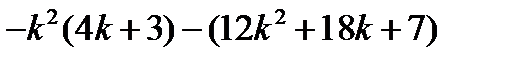 =
= 
 =
=  =
=  =
= 

Задачи на геометрическую прогрессию.
Пример 26.
Докажем, что общий член геометрической прогрессии равен
ап = а1∙q п-1, методом математической индукции.
1) Проверим, что данное утверждение верно при п=1:
a1= a1∙q0
a1 = a1∙1
a1 = a1
левая часть = правой части.
2) Предположим, что данное утверждение верно, при п=k:
a k = a1∙q k-1
3) И, докажем, что данное утверждение верно при п = k+1:
ak+1= a1∙qk
Доказательство:
a k+1 = ak ∙q = a1∙qk-1 ∙ q = a1∙qk,
что и требовалось доказать.
Оба условия принципа математической индукции выполняются и поэтому формула an=a1∙ qn-1 верна для любого натурального числа п.
Пример 27.
Методом математической индукции доказать, что сумма п - членов геометрической прогрессии вычисляется по формуле:
Sn =  (q≠1).
(q≠1).
1) Проверим, что данное утверждение верно при п=1:
Левая часть: S1=b1
Правая часть: 
b1 = b1.
2) Предположим, что данное утверждение верно, при п=k:
Sk = 
3)И, докажем, что данное утверждение верно при п=k+1:
Sk+1 =  .
.
Доказательство:
S k+1 = Sk+(k+1) член =
=  .
.
Оба условия принципа математической индукции выполняются, поэтому формула Sn=  верна для любого натурального п.
верна для любого натурального п.
Логические задачи.
Пример 28.
На доске написаны два числа 1; 1. Вписав между числами их сумму, мы получим числа 1; 2; 1. Повторив эту операцию ещё раз, получим числа 1; 3; 2; 3; 1. После трёх операций будут числа 1; 4; 3; 5; 2; 5; 3; 4; 1. Какова будет сумма всех чисел на доске после 100 операций?
Решение. Ясно, что для выполнения 100 операций нам не хватит ни места, ни времени. Значит, нужно пытаться найти какую-то общую формулу для суммы чисел после n операций (обозначим её Sn). Посмотрим на таблицу и найдем закономерность.
| n | Sn |
На самом деле можно не выписывать числа, а сразу сказать, как изменится сумма после добавления новых чисел. Пусть сумма была равна S. Разобьём каждое новое число в сумму двух старых. Например, от
1; 3; 2; 3; 1
мы переходим к
1; 1 + 3; 3; 3 + 2; 2; 2 + 3; 3; 3 + 1; 1:
Каждое старое число (кроме двух крайних единиц) входит теперь в сумму три раза, поэтому новая сумма равна 3S − 2 (мы вычли 2, чтобы учесть недостающие единицы). Поэтому S5 = 3S4 − 2 = 244 и вообще Sn = 3Sn−1 − 2: Попробуем составить общую формулу. Если бы не вычитание двух единиц, то каждый раз сумма увеличивалась бы в три раза, как в степенях тройки (1; 3; 9; 27; 81; 243;:::). А наши числа, как теперь видно, на единицу больше. Таким образом, можно предположить, что Sn = 3n + 1. Докажем это по индукции.
1) N=1. Смотри таблицу (для n = 0; 1; 2; 3).
2) Если Sn−1 = 3n−1 + 1; то Sn = 3Sn−1 − 2 = 3(3n−1 + 1) − 2 = 3 · 3n−1 + 3 − 2 = 3n + 1, что и требовалось доказать. Из формулы видно, что после ста операций сумма всех чисел на доске будет равна 3100 + 1. Задача решена.
Пример 29.
 Несколько прямых делят плоскость на части. Доказать, что можно раскрасить эти части в белый и чёрный цвет так, чтобы соседние части (имеющие общий отрезок границы) были разного цвета.
Несколько прямых делят плоскость на части. Доказать, что можно раскрасить эти части в белый и чёрный цвет так, чтобы соседние части (имеющие общий отрезок границы) были разного цвета.
 Заметим, что не любую картинку можно так раскрасить. Например, если в одной точке сходятся несколько прямых, то одна из них может быть белой, а две другие, хоть и граничат между собой, будут черными. Но для плоскости, разделенной на части прямыми,
Заметим, что не любую картинку можно так раскрасить. Например, если в одной точке сходятся несколько прямых, то одна из них может быть белой, а две другие, хоть и граничат между собой, будут черными. Но для плоскости, разделенной на части прямыми,
 это произойти не может. Докажем это.
это произойти не может. Докажем это.
Пусть прямая только одна. Тогда всё просто: одна полуплоскость белая, другая – чёрная.
Если прямых две, получатся четыре части. Посмотрим, что произойдёт, если мы на рисунке с двумя прямыми и четырьмя частями проведём третью прямую. Она поделит три части из четырёх; при этом появятся новые участки границы, по обе стороны
 которых цвет один и тот же. Что же делать? С одной стороны от новой прямой поменяем цвета (белый на черный и наоборот) и получим раскраску, соответствующую условию. Тогда, используя этот метод, мы можем добавить еще сколько угодно прямых. Что и требовалось доказать.
которых цвет один и тот же. Что же делать? С одной стороны от новой прямой поменяем цвета (белый на черный и наоборот) и получим раскраску, соответствующую условию. Тогда, используя этот метод, мы можем добавить еще сколько угодно прямых. Что и требовалось доказать.

Пример 30.
 Игрушка («Ханойские башни») имеет три стержня. На одном находится пирамидка из нескольких колец уменьшающихся снизу-вверх). Эту пирамидку нужно переложить на другой стержень, соблюдая правила игры: нельзя переносить сразу несколько колец и нельзя класть большее кольцо поверх меньшего. Например, пирамидку из двух колец можно переложить так: положить меньшее кольцо на второй стержень, затем большее на третий, а затем меньшее поверх большего (1 – 2, 1 – 3, 2 – 3, если стержни нумеровать слева направо).
Игрушка («Ханойские башни») имеет три стержня. На одном находится пирамидка из нескольких колец уменьшающихся снизу-вверх). Эту пирамидку нужно переложить на другой стержень, соблюдая правила игры: нельзя переносить сразу несколько колец и нельзя класть большее кольцо поверх меньшего. Например, пирамидку из двух колец можно переложить так: положить меньшее кольцо на второй стержень, затем большее на третий, а затем меньшее поверх большего (1 – 2, 1 – 3, 2 – 3, если стержни нумеровать слева направо).
 Наша задача доказать, что возможно переместить на другой стержень пирамидку из любого числа колец, соблюдая правила игры.
Наша задача доказать, что возможно переместить на другой стержень пирамидку из любого числа колец, соблюдая правила игры.
Пусть в пирамидке три кольца. Временно забудем про нижнее, самое большое (мысленно приклеим его к основанию). Тогда останется пирамидка из двух колец, которую мы уже умеем перекладывать. Переложим её с первого стержня на третий. После этого вспомним про большое кольцо и переложим его на второй стержень (который пока пуст). Теперь переложим пирамидку из двух верхних колец с третьего стержня на второй. Теперь, зная, как перекладывать пирамидку из трех колец, мы можем переложить четыре кольца (достаточно в наших предыдущих рассуждениях заменить пирамидку из двух колец на пирамидку из трёх). После этого можно переложить пять колец, зная, как перекладывать четыре кольца, и так далее. Что и требовалось доказать.
Геометрические задачи.
Пример 31.
Найти, на сколько частей делит прямую n точек.
Рассмотрим 1 точку. Она делит прямую на 2 части. 2 точки делят прямую на 3 части, 3 точки на 4 части. Тогда мы можем предположить, что n точек делят прямую на N(n)=n+1 частей. Докажем это утверждение.
1) При n=1. Верно, так как мы рассмотрели это в рассуждениях.
2) Если добавленная точка расположена между какими то двумя, она разделит соединяющий эти точки отрезок на два. Если она расположена на луче, она добавит один отрезок. То есть добавление точки увеличивает число частей на 1. Значит: N(n+1)=N(n)+1=(n+1)+1. Следовательно, наше утверждение доказано.
Пример 32.
Доказать, что сумма внутренних углов любого n-угольника равна π(n-2).
Так как минимальный n-угольник – это треугольник, то на нашу задачу накладывается условие: n≥3.
1)  При n=3. π*1=π – верно.
При n=3. π*1=π – верно.
2) При n=k. π(k-2) – верно.
3) При n=k+1. π(k-1). Разобьем (k+1)-угольник на треугольник и k-угольник, проведя диагональ. Тогда сумма углов треугольника и
4) k-угольника равна π(n-2) (из 1 и 2 шага). Следовательно, сумма внутренних углов любого n-угольника равна π(n-2), что и требовалось доказать.
Пример 33.
Вычислить сторону  правильного
правильного  - угольника, вписанного в круг радиуса R.
- угольника, вписанного в круг радиуса R.
Решение.
При n=2 правильный 2n – угольник есть квадрат; его сторона  . Далее, согласно формуле удвоения
. Далее, согласно формуле удвоения

находим, что сторона правильного восьмиугольника  , сторона правильного шестнадцатиугольника
, сторона правильного шестнадцатиугольника  , сторона правильного тридцатидвухугольника
, сторона правильного тридцатидвухугольника  . Можно предположить поэтому, что сторона правильного вписанного 2n – угольника при любом
. Можно предположить поэтому, что сторона правильного вписанного 2n – угольника при любом  равна
равна
 . (1)
. (1)
Допустим, что сторона правильного вписанного  - угольника выражается формулой (1). В таком случае по формуле удвоения
- угольника выражается формулой (1). В таком случае по формуле удвоения
 ,
,
откуда следует, что формула (1) справедлива при всех n.
Пример 34.
На сколько треугольников n-угольник (не обязательно выпуклый) может быть разбит своими непересекающимися диагоналями?
Решение.
Для треугольника это число равно единице (в треугольнике нельзя провести ни одной диагонали); для четырехугольника это число равно, очевидно, двум.
Предположим, что мы уже знаем, что каждый k-угольник, где k<n, разбивается непересекающимися диагоналями на k-2 треугольника (независимо от способа разбиения). Рассмотрим одно из разбиений n-угольника А1А2…Аn на треугольники.

Пусть А1Аk – одна из диагоналей этого разбиения; она делит n-угольник А1А2…Аn на k-угольник A1A2…Ak и (n-k+2)-угольник А1АkAk+1…An. В силу сделанного предположения, общее число треугольников разбиения будет равно
(k-2)+[(n-k+2)-2]=n-2;
тем самым наше утверждение доказано для всех n.
Заключение
Итак, индукция одна из форм умозаключения, приём исследования, применяя который от знания отдельных фактов приходят к общим положениям. Индукция бывает полная и неполная. Метод неполной индукции состоит в переходе к универсальной формулировке после проверки истинности частных формулировок для отдельных, но не всех значений n. Применяя полную индукцию, мы лишь тогда считаем себя вправе объявить об истинности универсальной формулировки, когда убедились в её истинности для каждого без исключения значения n. Метод математической индукции – метод доказательства, основанный на принципе математической индукции. Он позволяет в поисках общего закона испытывать гипотезы, отбрасывать ложные и утверждать истинные.
Метод математической индукции является одной из теоретических основ при решении задач на суммирование, доказательстве тождеств, доказательстве и решении неравенств, решении вопроса делимости, при изучении свойств числовых последовательностей, при решении геометрических задач и т. д.
Вывод:
В ходе проделанной работы я изучила и проанализировала множество материалов по данной теме. Я выполнила поставленные перед собой цели и задачи.
Метод математической индукции, действительно, можно применить при решении различного рода задач в школе, а также при подготовке к ЕГЭ. Достоинством метода математической индукции является его универсальность, так как с помощью этого метода можно решить многие задачи. Недостатком неполной индукции является то, что порой она приводит к ошибочным выводам. Обобщив и систематизировав знания по математической индукции, я убедилась в необходимости знаний данного метод. Кроме того, эти знания повышают интерес к математике, как к науке.
Список литературы
1. Виленкин Н. Я., Шибасов Л. П., Шибасова З. Ф. За страницами учебника математики. Москва: Просвещение, 1996г.
2. Депман И.Я. Метод математической индукции. Пособие для учителей. Ленинград: Печатный двор, 1957г.
3. Соминский И.С. Метод математической индукции. Популярные лекции по математике, выпуск 3-М.: Наука, 1974г.
4. Шахмейстер А.Х. Математическая индукция. М.: Издательство МЦНМО, 2018.-396с.
5. Шень А. Математическая индукция. 6-е изд., дополн. - М.: МЦНМО, 2016. - 32 с.: ил.
6. Математическая индукция [Электронный ресурс]. - Режим доступа: https://ru.wikipedia.org/wiki/Математическая_индукция, свободный – (30.04.2019).