Метод математической индукции состоит в следующем. Пусть нужно доказать справедливость некоторого утверждения А(n) для любого натурального числа n (например, нужно доказать, что сумма первых n нечётных чисел равна n2). Сначала проверяют справедливость утверждения для n = 1 (базис математической индукции). Затем доказывают, что для любого натурального числа k верно следующее утверждение: если справедливо A(k), то справедливо и A(k+1) (индукционный шаг). Тогда утверждение А(n) считается доказанным для любого n. В самом деле, утверждение справедливо для n = 1 (это проверялось отдельно). Но если верно А(1), то верно и А(2); поскольку верно А(2), то верно и А(3); из справедливость А(3) следует, что утверждение верно и для n = 4 и т.д., т.е. утверждение верно для любого n.
Обобщая сказанное, сформулируем следующий общий принцип, который обычно считают одной из аксиом множества натуральных чисел.
Утверждение, зависящее от натурального числа n, справедливо для любого n, если выполнены два условия:
А) утверждение верно для n =1;
Б)из справедливости утверждения для n = к, где к – любое натуральное число, вытекает справедливость утверждения и для следующего натурального числа n= к+1.
Так же, если предложение А(n), зависящее от натурального числа n, истинно для n=1 и из того, что оно истинно для n=k (где k-любое натуральное число), следует, что оно истинно и для следующего числа n=k+1, то предположение А(n) истинно для любого натурального числа n.
Алгоритм (он состоит из четырех этапов):
1.база (показываем, что доказываемое утверждение верно для некоторых простейших частных случаев (п = 1));
2.предположение (предполагаем, что утверждение доказано для первых к случаям);
3. шаг (в этом предположении доказываем утверждение для случая п = к + 1);
|
|
4.вывод (утверждение верно для всех случаев, то есть для всех п).
Второй вариант метода математической индукции.
Некоторые утверждения справедливы не для всех натуральных п, а лишь для натуральных п, начиная с некоторого числа р. Такие утверждения иногда удается доказать методом, несколько отличным от того, который описан выше, но вполне аналогичным ему. Состоит он в следующем.
Утверждение верно при всех натуральных значениях п ≥ р, если: 1)оно верно при п =р (а не при п = 1, как было сказано выше);
2)из справедливости этого утверждения при п = k , где k ≥ р (а не k ≥ 1, как сказано выше), вытекает, что оно верно и при п = k + 1.
Пример: Докажите, что для любого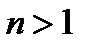 
справедливо равенство
Обозначим произведение в левой части равенства через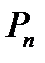 
, т.е.
мы должны доказать, что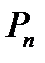 
.
Для n=1 формула не верна (1- 1) = 1(неверно).
1) Проверим, что эта формула верна для n = 2. 
, 
- верно.
2) Пусть формула верна для n = k, т.е. 
3) Докажем, что это тождество верно и для n = k + 1, т.е.
По принципу математической индукции равенство справедливо для любого натурального .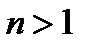
Глава 2. Задачи на использование метода математической индукции
Доказательства неравенств.
Пример 1.
Доказать, что при любом натуральном n>1
.
Решение.
Обозначим левую часть неравенства через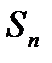 
.
, следовательно, при n=2 неравенство справедливо.
Пусть 
при некотором k. Докажем, что тогда и 
. Имеем 
, 
.
Сравнивая 
и 
, имеем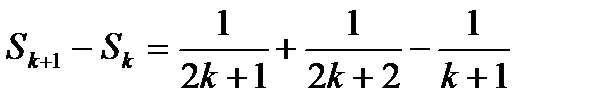 
, т.е. 
.
При любом натуральном k правая часть последнего равенства положительна. Поэтому 
. Но 
, значит, и .
|
|
Пример 2.
Докажем, что 2n+1>2n+1 для любого n {\displaystyle x\in \mathbb {N} }∈ N.
Доказательство
Пусть n=1. Тогда 22>2+1; 4>3 – истина.
Пусть k – истина, т.е. 2k+1>2k+1.
Докажем, что тогда и k+1 – истина, т.е. 2k+2>2k+3.
По индуктивному предположению 2k+1>2k+1.
Умножим обе части неравенства на 2:
2∙2k+1>2(2k+1)> (2k+3) + (2k−1).
Отметим, что если a > b + c, то a > b при c > 0.
Следовательно, 2k−1 > 0. Тогда при k > 1 2k+2>2k+3.
Итак, доказано что при n=1и k – истина следует, что k+1 – истина.
Таким образом, для любого n {\displaystyle x\in \mathbb {N} }∈ N 2n+1>2n+1 истина
Пример 3.
Доказать, что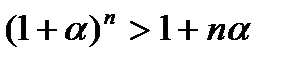 
, где 
>-1,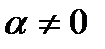 
, n – натуральное число,
большее 1.
Решение.
При n=2 неравенство справедливо, так как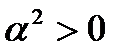 
.
Пусть неравенство справедливо при n=k, где k – некоторое натуральное число, т.е.
. (1)
Покажем, что тогда неравенство справедливо и при n=k+1, т.е.
. (2)
Действительно, по условию, 
, поэтому справедливо неравенство
, (3)
полученное из неравенства (1) умножением каждой части его на 
. Перепишем неравенство (3) так: 
. Отбросив в правой части последнего неравенства положительное слагаемое 
, получим справедливое неравенство (2).
Пример 4.
Пусть х1, х2,..., хn — произвольные положительные числа, причем
x1x2…xn = 1. Доказать, что х1 + х2 +... +хn ≥ n.
1. Если n = 1, то по условию х1 = 1 и, следовательно, можно написать x1 ≥ 1, т. е. для n = 1 утверждение верно.
2. Предположим, что утверждение верно для n = k. Пусть х1,х2,...,хk,хk + 1 - произвольные положительные числа и
х1х2…хkхk+1 = 1.
Могут представиться два случая: либо все эти числа равны 1, и тогда их сумма равна k+1 и неравенство доказано, либо среди этих чисел есть хотя бы одно число, не равное единице, и тогда обязательно есть, по крайней мере, еще одно число, не равное единице, причем если одно из них меньше единицы, то другое больше единицы. Не ограничивая общности, можно считать, что хk > 1, а хk + 1 < 1. Рассмотрим теперь k чисел
|
|
x1, x2,…, xk-1, (xkxk+1).
Произведение их равно единице, и, следовательно, по индуктивному предположению
x1 + x2 + … + xk-1+ xkxk+1 ≥ k.
Прибавим к обеим частям последнего неравенства хk+хk+1, перенесем xkxk+1направо и преобразуем правую часть неравенства:
x1 + x2 + … + xk + xk+1 ≥ k - xkxk+1+хk + хk+1 =
= k+1 +хk(1-хk+1) + хk+1- 1=k+1+хk(1- хk+1) - (1 - хk+1) =
= k + 1+(1 - хk+1)(xk - l) ≥ k + l.
Таким образом, из истинности утверждения при n = k вытекает его истинность при n = k+ 1. Утверждение доказано. Из приведенного доказательства следует, что знак равенства в доказываемом соотношении имеет место тогда и только тогда, когда x1 = х2 =... = хn = 1
Пример 5.
Неравенство Бернулли
Приведем доказательство Бернулли.
(1+α)n > 1 + nα, где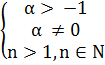 
Пусть n = 2.
(1+α)2 > 1+2α; α2 > 0, значит n = 2 – истина.
Пусть k – истина, т.е. (1+α)k > 1+kα.
Докажем, что k+1 - истина, т.е. (1+α)k+1 > 1+(k+1)α.
По индукционному предположению (1+α)k > 1+kα.
Умножим обе части неравенства на 1+α, тогда
(1+α)k+1 > (1+kα)(1+α) = 1+(k+1)α+ kα 2>1+(k+1)α, так как kα 2>0.
Значит, (1+α)k+1 > 1+(k+1)α, т.е. k+1 - истина.
Итак, доказано, что при n=1и k – истина следует, что k+1 – истина.
Таким образом, для любого 
(n 
2) при α > -1 и α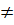 
0, n – истина, т.е.
(1+α)n > 1 + nα, где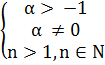
Пример 6.
Доказать неравенство 
, при a и b≥0.
1) При n=1. a+b≤ 2(a+b) – верно.
2) При n=k. 
.
3) При n=l+1. 
= 
так как разность 
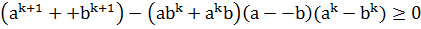и, следовательно, 
. Что и требовалось доказать.
2. Суммирование рядов .
Пример 7.
Пусть дана последовательность (n) натуральных чисел. Найдем формулу вычисления суммы первых n чисел:
S(n)=l+2 + 3 +... + n.
Решение.
Рассмотрим S(1), S(2), S(3), S(4). Мы имеем:
S(l)=l,
S(2)=1+2 = 3,
S(3)=1+2 + 3 = 6,
S(4)=1+2 + 3 + 4=10.
Заметив, что полученные числа можно записать в виде
естественно сделать предположение, что
Применим теперь метод математической индукции для доказательства полученной формулы (1).
При n = 1, 
Формула верна при n = 1. Предположим, что формула верна при n = k > 1:
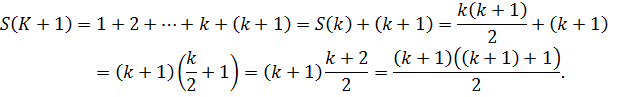
'Значит, из справедливости формулы для n = k вытекает ее справедливость для n = k + 1. По принципу математической индукции отсюда вытекает справедливость формулы (1) для всех натуральных значений n.
В некоторых случаях для доказательства тождества Р(n) = Q (n)можем сначала убедиться, что Р (1) = Q (1), и, предполагая справедливость равенства P(k)=Q(k), k>1, доказать тождество P(k + 1) = Q(k + 1). Тогда из истинности равенства P(k) = Q(k) будет следовать истинность равенства P(k + 1) = Q(k + 1) и по принципу математической индукции будет следовать истинность тождества P(n)=Q(n)для всех n.
Пример 8.
Доказать, что сумма квадратов n первых чисел натурального ряда равна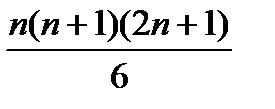 
.
Решение.
Пусть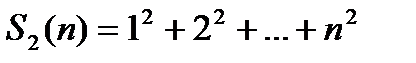 
.
.
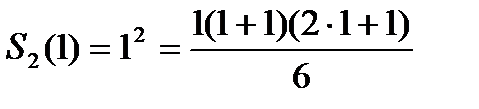Предположим, что 
. Тогда
и окончательно 
.
Пример 9.
Доказать, что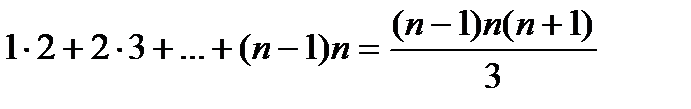 
.
Решение.
.
Если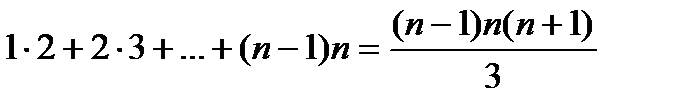 
, то
.
Пример 10.
Доказать, что
.
Решение.
При n=1 гипотеза очевидно верна.
Пусть 
.
Докажем, что 
.
Действительно,
Пример 11.
Найдите сумму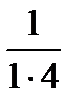 
+ 
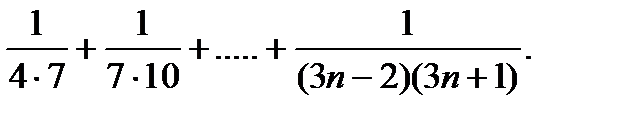
S(1)= 
, S(2)=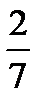 
, S(3)=S(2)+ 
, S(4)=S(3)+ 
, S(5)=S(4)+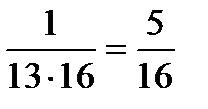 
, S(6)=S(5)+ 
Можно предположить, что S(n)= 
Докажем это. Для n=1 формула верна. Предположим, что она будет верна и для n=k+1:
Пример 12.
Доказать, что 1+x2+x3+x4+….+xn= 
, где x 
1
Решение.
, следовательно, при n=1 формула верна.
Пусть k- любое натуральное число и пусть формула верна при n=k, т.е.
Докажем тогда
В самом деле,
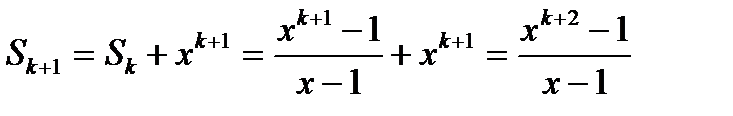
Значит, по принципу математической индукции формула верна для любого натурального n.
Задачи на делимость.
Пример 13 .
Если n – натуральное число, то число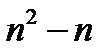 
четное.
При n=1 наше утверждение истинно: 
- четное число. Предположим, что 
- четное число. Так как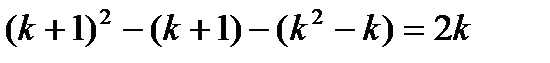 
, a 2k – четное число, то и 
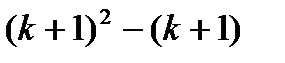четное. Итак, четность 
доказана при n=1, из четности 
выведена четность 
.Значит,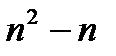 
четно при всех натуральных значениях n.
Пример 14.
Доказать истинность предложения
A(n)={число 5∙23n-2+33n-1 кратно 19}, n – натуральное число.
Решение.
Высказывание А(1)={число 
кратно 19} истинно.
Предположим, что для некоторого значения n=k
А(k)={число 5∙23k−2+33k−1 кратно 19} истинно. Тогда, так как
5∙23(k+1)−2+33(k+1)−1=8∙5∙23k+2+27∙33k−1=8(5∙23k−2+33k+1)+19∙33k−1, очевидно, что и A(k+1) истинно. Действительно, первое слагаемое делится на 19 в силу предположения, что A(k) истинно; второе слагаемое тоже делится на 19, потому что содержит множитель 19. Оба условия принципа математической индукции выполнены, следовательно, предложение A(n) истинно при всех значениях n.
Пример 15.
Доказать, что 10 п + 18 п – 28 кратно 27, где п- натуральное число.
1) Проверим, что данное утверждение верно при п=1:
10 1+ 18 – 28 = 10+18-28 = 0, 0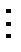 
27,
утверждение верно при п =1.
2)Предположим, что данное утверждение верно, при п=k:
(10 k +18k - 28) 
27
3)И, докажем, что данное утверждение верно при п=k+1:
(10 k+1+18(k+1)-28)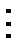 
27.
Доказательство:
10 k+1+18k+18-28=10 k ∙10+18k -10 = 10(10k+18k-28)-162k+270=
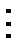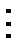= 10(10 k +18k – 28) - 27(6k-10), (10 k+1+18(k+1)-28) 27.
27 27
Так как данное утверждение верно при п=k и п = k+1 следовательно (10 п + 18 п – 28) делитсяна 27 прилюбом натуральном п.
Пример 16.
Доказать, что п3 +11п делится на 6, где п – натуральное число.
1) Проверим, что данное утверждение верно при п=1:
13+11∙1= 1+11= 12, 12 
6.
2) Предположим, что данное утверждение верно, при п=k:
(k3+11k) 
6.
3) И, докажем, что данное утверждение верно при п=k+1:
((k+1)3+ 11(k+1)) 6.
Доказательство:
(k+1)3+ 11(k+1)=(k3+3k2∙1+3k∙12+13)+11k+11=k3+3k2+3k+1+11k+11=
= k3+3k2+14k+12=(k3+11k)+(3k2+3k+12)=(k3+11k)+3(k2+k)+12 =((k3+11k)+3k(k+1)+12), отсюда
6 3, 2 6
(k+1)3+ 11(k+1) делится на 6.
Так как данное утверждение верно при п=1 и доказано, что верно при n=k+1 следовательно n3+11k делится на 6 при любом натуральном n.
Пример 17.
Доказать, что (11n+2+122n+1) кратно 133.
1) При n =1. 113+123=(11+12)(113-132+123)=23 
133. Так как (23∙133) кратно 133, то и (113+123) кратно 133.
2) При n=k. (11k+2+122k+1) кратно 133.
3) При n=k+1. Доказать, что (11k+3+122k+3) кратно 133.
11k+3+122k+3=11∙11k+2+122∙122k+1=11(11k+2+122k+1)+133∙122k+1.
В данном выражении второе слагаемое кратно 133, а первое слагаемое кратно 133 из второго пункта. Тогда по свойству делимости полученная сумма кратна 133, значит (11n+2+122n+1) кратно 133, что и требовалось доказать.
Пример 18.
Доказать, что (n3+3n2+8n) кратно 3.
1) При n=1. 1+3+8=12, 12 кратно 3 – верно.
2) При n=k. (k3+3k2+8k) кратно 3 – верно.
3) При n=k+1. Доказать, что ((k+1)3+3(k+1)2+8(k+1)) кратно 3.
(k+1)3+3(k+1)2+8(k+1)=k3+3k2+3k+1+3k2+k+1+8k+8=(k3+3k2+8k)+3k2+9k+9. Полученное выражение кратно 3, так как каждое из слагаемых кратно 3. Значит (n3+3n2+8n) кратно 3, что и требовалось доказать.
Пример 19.
Доказать, что (22n+1+1) кратно 3.
1) При n=1. 23+1=8+1=9, кратно 3 – верно.
2) При n=k. (22k+1+1) кратно 3 – верно.
3) При n=k+1. Доказать, что (22k+3+1) кратно 3.
22k+3+1=22k+1∙22+1=22k+1∙22+22-3=22(22k+1+1)-3. Полученное выражение кратно 3, так как каждое из слагаемых кратно 3. Значит (22n+1+1) кратно 3, что и требовалось доказать.