Методика обработки полной информации
Рассмотрим методику обработки полной информации по показателям надежности на примере двигателя.
Информация обрабатывается в следующем порядке.
Определяем количество отказов в интервале от 2700 до 4100 мото-ч.
Таблица 1.1 – Сводная ведомость по межремонтному ресурсу дизеля СМД.
| № | Ресурс, мото-ч | № | Ресурс, мото-ч | № | Ресурс, мото-ч | № | Ресурс, мото-ч |
Составление статистического ряда
Статистический ряд исходной информации для упрощения дальнейших расчетов составляют в том случае, когда повторность информации N>25. При N<25 статистический ряд не составляют.
В нашем примере повторность информации N=35>25, поэтому целесообразно составить статистический ряд, при этом информация разбивается на n–равных промежутков (интервалов), каждый из последующих должен прилегать к предыдущему без разрыва. Число интервалов статистического ряда:
где N – количество информации; n=√40±1=7 интервалов
Длина интервала:
A= 
где: tmax, tmin – наибольшее и наименьшее значение показателя надежности в сводной таблице информации. В нашем случае.
А= 
=975 мото-ч
Таблица 2.1 – Статистический ряд
| Интервал, мотто-ч | 0… | 1000… | 2000… | 3000… | 4000… | 5000… | 6000… |
| Середина интервала | |||||||
| Опытная частота, mi | |||||||
| Опытная вероятность, Pi | 0,05 | 0,1 | 0,2 | 0,25 | 0,2 | 0,15 | 0,05 |
Накопленная вероятность,
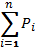
| 0,05 | 0,15 | 0,35 | 0,6 | 0,8 | 0,95 |
|
|
В первой строке указывают границы интервалов в единицах показателя надежности; во второй – середины интервалов; в третей – число случаев (опытную частоту mi), попадающих в каждый интервал. Если точка информации попадает на границу интервалов, то в предыдущий и последующие интервалы вносят 0,5 точки; в четвертой строке – опытную вероятность pi; в пятой – накопленную опытную вероятность
3 Определение среднего значения показателя надежности и среднего квадратичного отклонения
При наличии статистического ряда (при N>25), среднее значение показателя надежности
где: n – число интервалов в статистическом ряду,
tci – значение середины i – го интервала,
Pi – опытная вероятность i – го интервала.
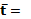500*0,05+1500*0,1+2500*0,2+3500*0,25+4500*0,2+5500*0,15+6500*0,05 = 3600 мото-ч
Среднее квадратичное отклонение при наличии статистического ряда определяется по формуле:
,
δ= 
=1513 мото-ч.
Проверка информации на выпадающие точки.
Грубую проверку на выпадающие точки проводят по правилу 3 σ
3σ
Нижняя граница: 
3 σ = 3600 – 3*1513 =0
Верхняя граница: 
3 σ = 3613+3*1513= 8139
Более точная информация на выпадающие точки проверяют по критерию Ирвина λ, теоретическое значение которого λT приведено в приложении 1.
Фактическое значение критерия:
λ оп = 
λ оп1 = 
= 0,56
λ оп2 = 
= 0,26
По приложению 1 находим, что при повторности информации N=40 и β=0,95, λT = 1,1. λT> λ оп значит выпадающих точек нет.
|
|
Определение коэффициента вариации.
Коэффициент вариации:
V = 
где: С – сдвиг (смещение) начала рассеивания показателя надежности.
При N>40, С = t – 0,5A, С = 0.
V = 
= 0,42
Выбор теоретического закона распределения для выравнивания опытной информации.
В первом приближении теоретический закон распределения выбирают по коэффициенту вариации. При V<0,30, выбирают ЗНР, при V>0,50 – ЗРВ. Если значение коэффициента вариации находится в интервале 0,30…0,50, то выбирают тот закон распределения, который лучше совпадает с распределением опытной информации. В нашем примере V=0,38, поэтому принимаем ЗРВ и ЗНР.