Дифференциальная функция:
где: A – длина интервала,
σ – среднее квадратическое отклонение,
tci – значение середины i – го интервала,
- среднее значение показателя надежности.
Кроме того, следует пользоваться уравнением
= 
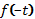Определим значение дифференциальной функции во всех интервалах статистического ряда
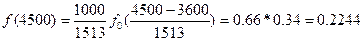
Интегралная функция:
= 
где: 
- значение окончания итого интервала.
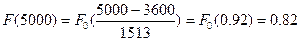
Таблица 7.1 – Значения дифференциальной и интегральной функции при ЗНР
| Интервал | 0… | 1000… | 2000… | 3000… | 4000… | 5000… | 6000… |
|
| 0,01 | 0,1 | 0,22 | 0,29 | 0,23 | 0,12 | 0,03 |
| 0,02 | 0,9 | 0,33 | 0,53 | 0,80 | 0,91 | 0,98 |
На основании полученных дифференциальных и интегральных функци 
й могут быть построены интегральные и дифференциальные кривые.
Дифференциальная кривая заменяет полигон, интегральная кривая заменяет кривую накопленных опытных вероятностей.
Использование для выравнивания распределения опытной информации закона распределения Вейбулла.
Дифференциальная функция:
где: a,b – параметры ЗРВ.
kb – коэффициент вариации.
Параметр kb определяют по таблице.
При V=0,42
kb=0,89
b=2,6
сb=0,34
Определим значение дифференциальной функции во всех интервалах статистического ряда.
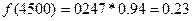
Интегральная функция:
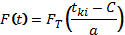
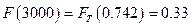
Таблица 7.1 – Значения дифференциальной и интегральной функции при ЗРВ
| Интервал | 0… | 1000… | 2000… | 3000… | 4000… | 5000… | 6000… |
|
| 0,01 | 0,1 | 0,22 | 0,29 | 0,23 | 0,12 | 0,03 |
|
| 0,02 | 0,9 | 0,33 | 0,53 | 0,80 | 0,91 | 0,98 |
8 Оценка совпадения опытного и теоретического законов распределения показателей надежности по критерию согласия Пирсона 
Критерий согласия Пирсона определяют:
где: ny – число интервалов в укрупненном статистическом ряду,
- опытная частота,
- теоретическая частота.
Таблица 8.1 – Укрупненный статистический ряд
| Интервал | ||||||
| mi | ||||||
| ЗНР | 
| 0.15 | 0.35 | 0.60 | 0.82 | 0.99 |
| F(t) | 8.8 | 6.8 | ||||
| ЗРВ |
| 0.09 | 0.33 | 0.53 | 0.80 | 0.98 |
| F(t) | 3.6 | 9.6 | 10.8 | 7.2 |
Критерий согласия Пирсона:
90%- при законе нормального распределения:
25%- при законе распределения Вейбула:
Принимаем ЗНР, т.к., что меньше при ЗРВ.
Для входа в таблицу, необходимо определить номер строки:
N=ny – k
где: ny – число интервалов в укрупненном статистическом ряду,
k – число обязательных связей
N=5 – 3=2
Тогда для ЗРВ Р=25%, для ЗНР Р=90%.
Следовательно, закон нормального распределения ЗНР подходит лучше. В дальнейшем будем пользоваться для определения средней величины износа, характеристики рассеивания и других пользователей для генеральной совокупности по закону ЗНР.
Определение доверительных границ рассеивания при законе нормального распределения.
Доверительные границы рассеивания одиночного зна 
чения показателя надежности при ЗНР определяют по уравнениям:
- нижняя доверительная граница:
– верхняя доверительная граница:
Определение абсолютной и относительной предельных ошибок переноса характеристик показателя надежности.
Наибольшая абсолютная ошибка переноса опытных характеристик показывает надежности при заданной доверительной вероятности равна по значению e β в обе стороны от среднего значения показателя надежности. От 
носительная предельная ошибка, %
11 Графики
ЗНР
N=40
0.3*40=12
В интервале наработки от 2500 до 4700 мото\ч будет 12 отказов.