| Многогранник | Вершин | Ребер | Граней |
| Тетраэдр | 4 треугольника | ||
| Куб (гексаэдр) | 6 квадратов | ||
| Октаэдр | 8 треугольников | ||
| Икосаэдр | 20 треугольников | ||
| Додекаэдр | 12 пятиугольников |
Для всех выпуклых многогранников выполняется теорема Эйлера: В – Р + Г = 2,
где В – число вершин, Р – число ребер, Г – число граней.
Ø Проверьте теорему для правильных многогранников!
Круглые тела (тела вращения)
Цилиндр
Цилиндр – это геометрическое тело, которое состоит из двух равных и параллельных кругов, и всех отрезков, соединяющих соответствующие точки этих кругов.
Круги называются основаниями цилиндра, а отрезки, соединяющие соответствующие точки окружностей кругов, − образующими цилиндра.
Цилиндр называется прямым, если его образующие перпендикулярны плоскостям оснований.
На рис. а) прямой цилиндр, б) наклонный цилиндр.
Вдальнейшем мы будем рассматривать только прямой цилиндр!
Круги с центрами О и О 1 – основания цилиндра.
АА 1, ВВ 1, СС 1 – образующие цилиндра.
Радиусом цилиндра называется радиус его основания (ОВ, О 1 В 1 – радиусы цилиндра).
Высотой цилиндра называется расстояние между основаниями.
Осью цилиндра называется прямая, проходящая через центры оснований (ОО 1).
Свойства цилиндра:
- основания цилиндра равны и параллельны;
- образующие цилиндра равны и параллельны.
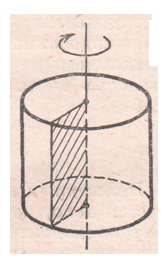
Цилиндр можно рассматривать как тело, полученное при вращении прямоугольника вокруг одной из его сторон.
Простейшие сечения цилиндра.
1. Осевое сечение цилиндра – это сечение цилиндра плоскостью, проходящей через его ось. Осевым сечением цилиндра является прямоугольник.
|
|
2. Сечение цилиндра плоскостью параллельной основанию.
В этом случае сечением является круг, равный и параллельный основанию.
Конус
Конус – это геометрическое тело, которое состоит из круга – основания конуса, точки, не лежащей в плоскости этого круга, − вершины конуса и всех отрезков, соединяющих вершину конуса с точками основания.
Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими конуса.
Конус называется прямым, если прямая, соединяющая вершину конуса с центром основания, перпендикулярна плоскости основания.
На рис. а) прямой конус, б) наклонный конус.
Вдальнейшем мы будем рассматривать только прямой конус!
S – вершина конуса.
Круг с центрами О – основание конуса.
SA, CB, SС – образующие конуса.
Высотой конуса называется перпендикуляр, опущенный из его вершины на плоскость основания.
Осью конуса называется прямая, содержащая его высоту (SО).
Свойства конуса:
- образующие конуса равны.
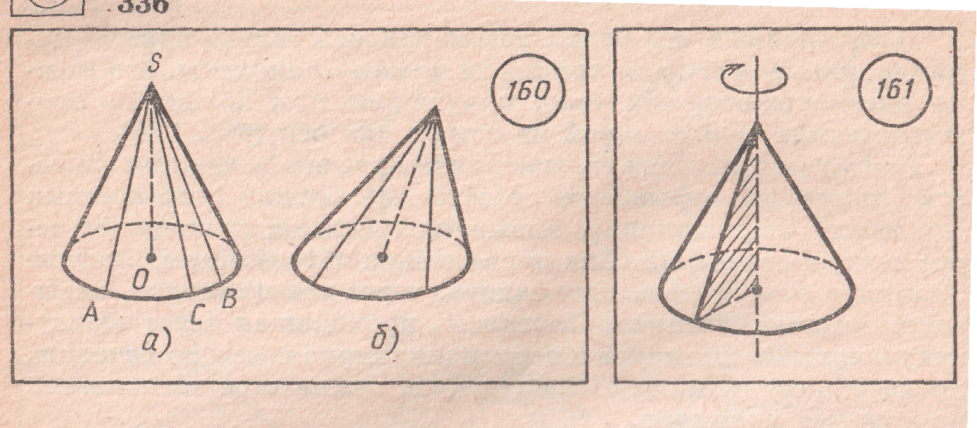
Конус можно рассматривать как тело, полученное при вращении прямоугольного треугольника вокруг его катета.
Простейшие сечения конуса.
1. Осевое сечение конуса – это сечение конуса плоскостью, проходящей через его ось. Осевым сечением конуса является треугольник.
2. Сечение конуса плоскостью параллельной основанию.
В этом случае сечением является круг, подобный и параллельный основанию.
Шар
Шар – это геометрическое тело, которое состоит из всех точек пространства, находящихся на расстоянии, не большем данного, от данной точки.
|
|
Эта точка (О) называется центром шара, а данное расстояние – радиусом шара.
Граница шара называется шаровой поверхностью или сферой.
Любой отрезок, соединяющий центр шара с точкой шаровой поверхности называется радиусом шара (OD, ОВ, ОА).
Диаметр шара – это отрезок, соединяющий две точки шаровой поверхности и проходящий через центр шара (АВ).
Свойства шара:
- радиусы шара равны;
- диаметры шара равны.
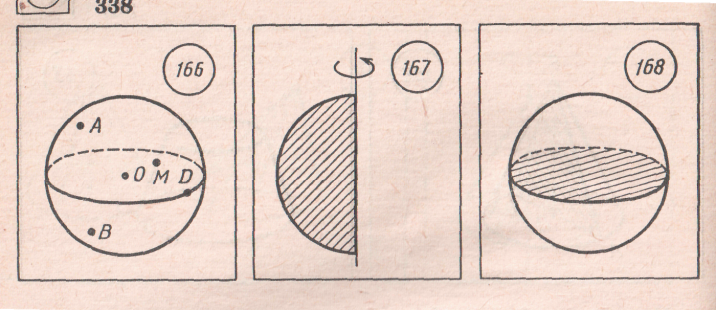
Шар можно рассматривать как тело, полученное при вращении полукруга вокруг его диаметра.
Простейшие сечения шара
1. Сечение шара плоскостью проходящей через его центр. В этом случае сечением является большой круг.
2. Сечение шара плоскостью не проходящей через его центр. В этом случае сечением является круг.