Ход урока
- Сообщение темы и цели урока
- Повторение и закрепление пройденного материала
Теоретический опрос
1. Сформулируйте определение квадратичной функции.
2. Сформулируйте свойства квадратичной функции у = а х2, где a >∞0.
3. Сформулируйте свойства квадратичной функции у = а х2, где а <0.
Функция y = ax 2
Определение. Квадратичной (квадратной) функцией называется функция вида
y = ax 2 + bx + c (a, b, c — числа, a ≠ 0)
с областью определения — множеством R всех действительных чисел.
Функция y = x 2 является частным случаем квадратичной функции y = ax 2 + bx + c при a = 1, b = 0, c = 0.
График квадратичной функции (как и график функции y = x 2) называется параболой, а уравнение y = ax 2 + bx + c (a ≠ 0) — уравнением этой параболы.
График квадратичной функции и его свойства мы будем изучать, используя свойства графика функции y = x 2.
При а ≠ 1, b = 0, c = 0 имеем еще один частный случай квадратичной функции y = ax 2 + bx + c, т. е. функцию
y = ax 2 (a ≠ 0, a ≠ 1).
Пусть a >0. Приведем два примера функции y = ax 2:
1) при a >1; 2) при 0< a <1.
Пример 1. Рассмотрим функцию y = 2 x 2 (здесь а = 2). Составим таблицу значений этой функции и сравним ее с таблицей значений функции y = x 2.
| x | ±0,5 | ±1 | ±1,5 | ±2 | |
| y = x 2 | 0,25 | 2,25 | |||
| y = 2 x 2 | 0,5 | 4,5 |
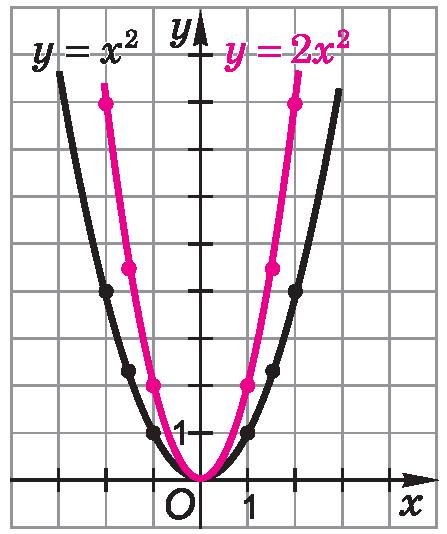
Рис.1.
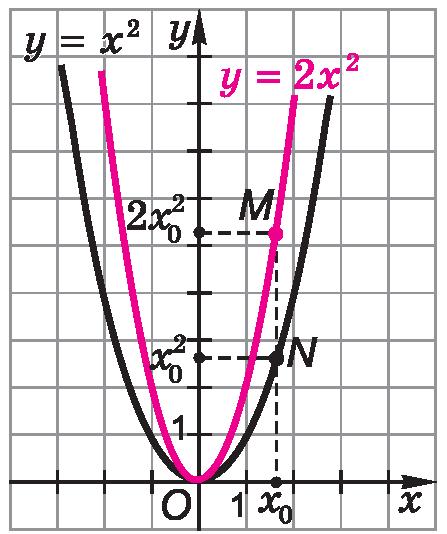
Рис.2
Используя данные таблицы, изобразим параболы y = x 2 и y = 2 x 2 в одной системе координат (ри.1).
Очевидно, что при каждом значении x значение функции y = 2 x 2 в 2 раза больше значения функции y = x 2. Значит, при одной и той же абсциссе x 0 ордината точки M на параболе y = 2 x 2 в 2 раза больше ординаты точки N на параболе y = x 2 (рис. 2). Поэтому любую точку M на параболе y = 2 x 2 можно получить из соответствующей точки N на параболе y = x 2, увеличив ординату точки N в 2 раза.
Говорят, что парабола y = 2 x 2 получается из параболы y = x 2 растяжением в 2 раза вдоль оси Oy. Заметим, что при растяжении параболы y = x 2 вдоль оси Oy ее вершина является неподвижной точкой (поясните почему).
Пример 2. Рассмотрим функцию y=12x2(здесь a=12 ). Составим таблицу значений этой функции и сравним ее с таблицей значений функции y = x 2.
| x | ±0,5 | ±1 | ±1,5 | ±2 | |
| y = x 2 | 0,25 | 2,25 | |||
| y = 12 x 2 | 0,125 | 0,5 | 1,125 |
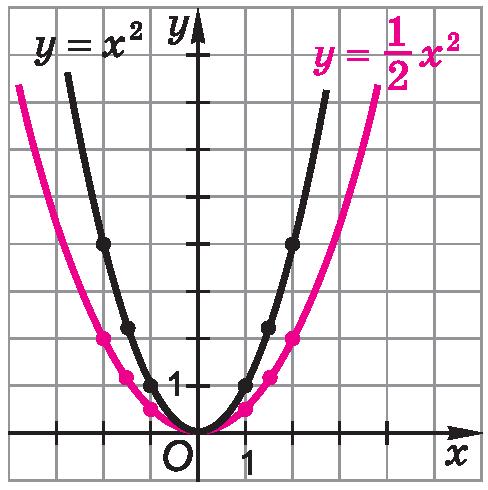
Рис. 3.
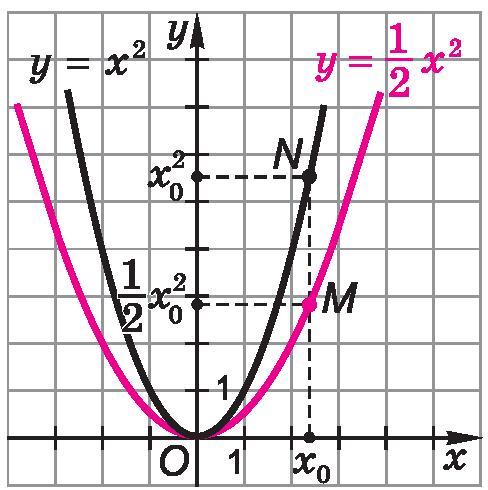
Рис. 4.
Используя данные таблицы, изобразим параболы y = x 2 и y=12x2 в одной системе координат (рис. 3).
Очевидно, что при каждом значении x значение функции y=12x2 в 2 раза меньше значения функции y = x 2. Значит, при одной и той же абсциссе x 0 ордината точки M на параболе y=12x2 в 2 раза меньше ординаты точки N на параболе y = x 2 (рис. 4). Поэтому любую точку M на параболе y=12x2 можно получить из соответствующей точки N на параболе y = x 2, уменьшив ординату точки N в 2 раза.
Говорят, что парабола y=12x2 получается из параболы y = x 2 сжатием в 2 раза вдоль оси Oy. Заметим, что при сжатии параболы y = x 2 вдоль оси Oy ее вершина является неподвижной точкой (поясните почему).
Вообще,
если a >1, то парабола y = ax 2 получается из параболы y = x 2 растяжением в a раз вдоль оси Oy;
если 0 < a < 1, то парабола y = ax 2 получается из параболы y = x 2 сжатием в 1a раз вдоль оси Oy.
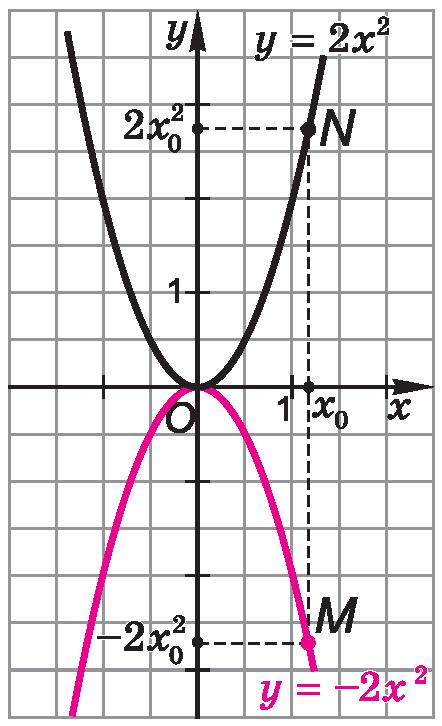
Рис. 5.
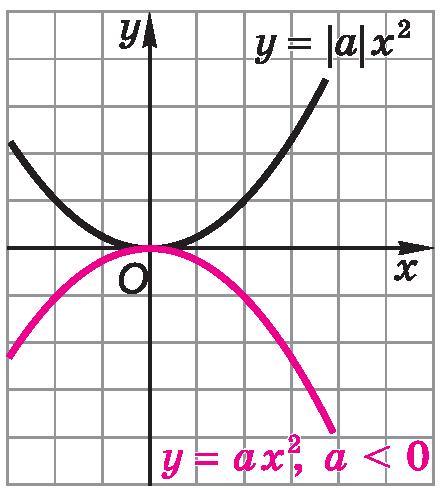
Рис. 6.
Функция y = ax 2 (a > 0) обладает теми же свойствами, что и функция y = x 2 (см. п. 6.1), и устанавливаются они так же, как для функции y = x 2.
Рассмотрим функцию y = ax 2 при a < 0.
В качестве примера приведем функцию y = −2 x 2. Сравним ее с функцией y = 2 x 2, которую мы уже изучили.
Заметим, что графики функций y = −2 x 2 и y = 2 x 2 симметричны относительно оси Ox (рис. 5).
Вообще, парабола y = ax 2 (a < 0) симметрична параболе y=| a |x2 относительно оси Ox (рис. 6). Из этой симметрии следуют свойства графика функции y = ax 2 (a < 0). Например, рассматриваемая парабола симметрична относительно оси ординат.
Таким образом, для параболы y = ax 2 при любом a ≠ 0 ось Oy является осью симметрии.
Точка, в которой график квадратичной функции y = ax 2 — парабола — пересекается со своей осью симметрии, называется вершиной параболы.
Вершиной параболы y = ax 2 (a ≠ 0) является начало координат.
Если a > 0, то ветви параболы y = ax 2 направлены вверх, а если а < 0, то ветви параболы направлены вниз.
Свойства


1) a > 0.
- Ветви параболы y = ax2 направлены вверх;
- Ось симметрии - ось OY;
- Вершина параболы - т. O (0,0);
- Наименьшее значение y = 0 функция y = ax2 принимает при x = 0. Наибольшего значения нет;
- Область значений функции y = ax2, т.е. все значения, которые принимает
y - [0; + ∞);
- При 0 < a < 1 парабола y = ax2 получается из параболы y = x2 сжатием к оси OX в 1/a раз;
- При a > 1 - растяжением y = x2 от оси OX в a раз.
2) a < 0.
- Ветви параболы y = ax2 направлены вниз;
- Парабола y = ax2 симметрична относительно оси OY параболе y = -ax2 (-a > 0);
- Наибольшее значение y = 0 функция y = ax2 принимает при x = 0. Наименьших значений нет;
- Область значений функции y = ax2 –(- ∞; 0 ].
- При 0 <a <1 парабола y = ax2 получается из параболы y = x2 сжатием к оси OX в 1/a раз;
- При a >1 - растяжением y = x2 от оси OX в a раз.
Пример 4.
Построим график функции 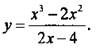
Область определения функции задается условием 2х - 4 ≠ 0, т. е. х ≠ 2. Разложим числитель и знаменатель дроби на множители и сократим ее. Получаем: 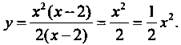
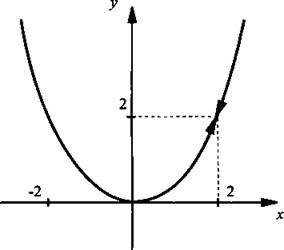
Построим параболу у = 1/2х2 и удалим из нее точку с абсциссой х = 2 (показана стрелками).
Пример 5
При каких значениях а парабола у = -1/2х2и прямая у = 3х + а не имеют общих точек?
Предположим, что данные линии имеют общую точку. Тогда ее координаты удовлетворяют системе уравнений 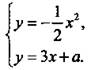
Попробуем решить эту систему. Так как в уравнениях левые части одинаковы, то равны и правые.
Получаем уравнение -1/2х2 = 3х + а, или 0 = х2 + 6х + 2а. На самом деле данные линии общих точек не имеют. Это означает, что полученное квадратное уравнение решений не имеет. Поэтому его дискриминант D = 36 - 8а < 0, откуда а > 36/8 = 4,5.
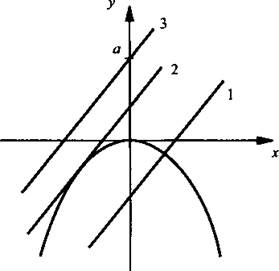
На рисунке приведена иллюстрация задачи. Очевидно, прямая у = 3х + а пересекает ось ординат в точке у = а. При увеличении а прямая смещается вверх параллельно самой себе. Выполненные расчеты показывают, что прямая при а < 4,5 пересекает параболу в двух точках (линия 1), при а = 4,5 касается параболы в одной точке (линия 2), при а > 4,5 не имеет общих точек с параболой (линия 3).
Контроль усвоения пройденного материала
(тест)
- Как называется график функции у = - 4х2?
а) прямая;
б) гипербола;
в) парабола.
- Ветви этой параболы направлены
а) вверх (a …0);
б) вниз (а …0).
3) Вершиной параболы является точка
а) 0;
б) (0;0);
в) (1; - 4).
4) На каком рисунке изображен график функции у = - 4х2?
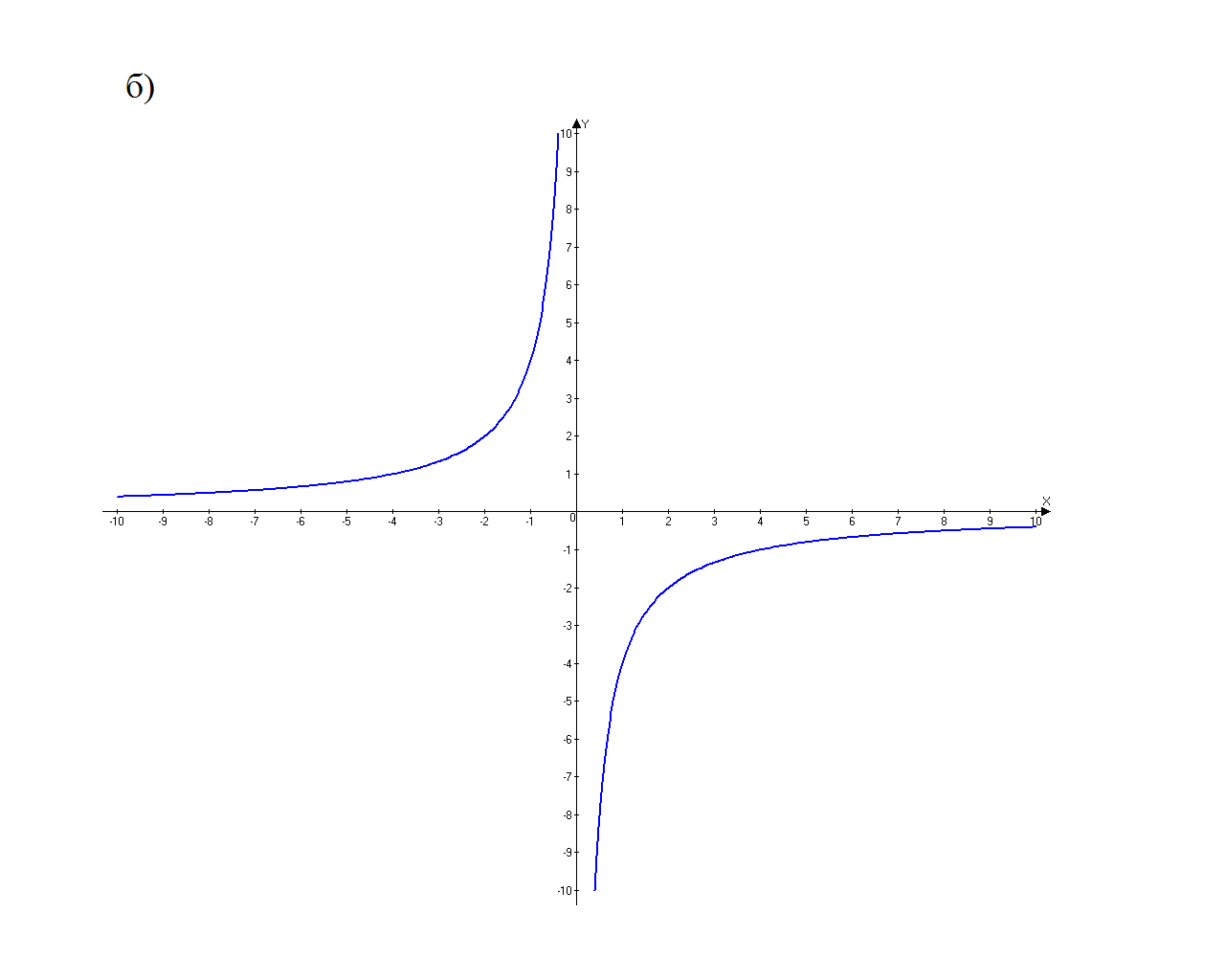
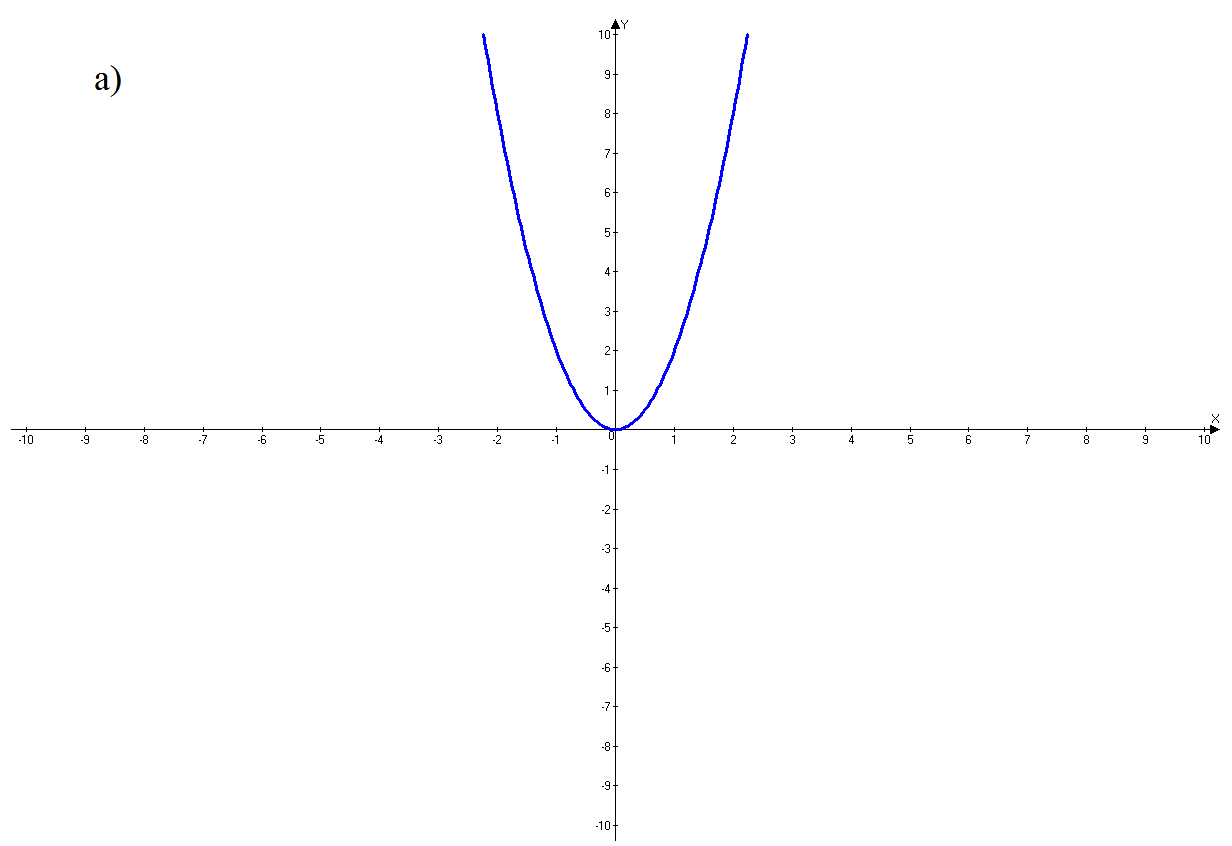
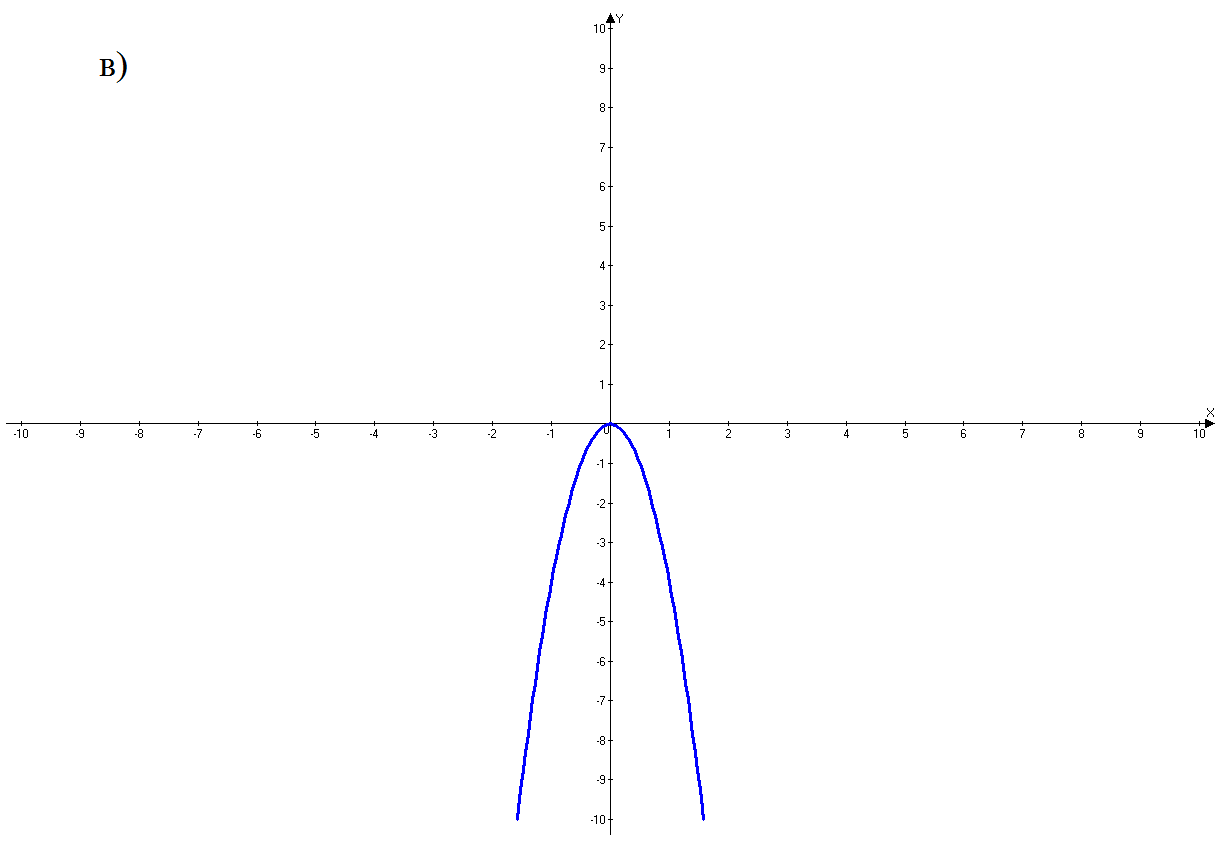
5) Какая точка принадлежит графику функции у = 3х2:
a) А (- 2; 12); б) В (5; 125); в) С (- 4; - 48).
6) Возрастает или убывает функция у = х2 на промежутке
(- 4; - 1)?
а) убывает; б) возрастает.
Тренировочные упражнения
1. Точка (4; - 48) принадлежит графику функции у = а х2. Чему равен коэффициент а?
Решение: - 48 = а 42; - 48 = а 16; а = - 3.
Ответ. -3.
2. Изобразите схематически графики функций у = 0,01х2 и у = 10х. Графики этих функций имеют общую точку О (0; 0). Имеют ли графики этих функций другие общие точки? При положительном ответе найдите координаты этих точек.
Решение:
Изобразив схематически графики функций видно, что они имеют две общие точки.
Приравняем значения функций
у = 0,01x2 и у = 10х; 0,01x2 = 10х; 0,01x2 - 10х = 0; x2 - 1000х = 0; x(х – 1000) = 0;
х1 = 0; х2 = 1000;
у1 =0; у2 = 10000.
Эти графики имеют две общие точки: О (0; 0) и
А (1000; 10000).
Ответ: имеют; А (1000; 10000).
Творческое задание
1. При каких значениях k прямая у = kх – 4 имеет только одну общую точку с параболой у = х2?
Решение:
Приравняем значения функций:
х2 = kх – 4, х2 - kх + 4 = 0.
Квадратное уравнение x2 - kх + 4 = 0 имеет единственное решение, если D = 0.
a = 1; b = - k; c = 4.
D = b2 - 4 a c; D = k2 – 16 = 0; k2 = 16;
k = 4 или k = - 4
Прямая у = kx – 4 имеет только одну общую точку с параболой у = x2, если k = 4 или k = - 4.
Ответ: 4; - 4.
Удивительная парабола
Учитель: «Ребята, вы научились строить график функцииу= а x2. Характерный облик параболы известен всем, но параболу можно встретить не только на уроках алгебры.
Форму параболы принимает струя воды, бьющая из шланга или фонтана (слайд 2, 3).
По параболе летит мяч или брошенный камень. Действительно, в баскетболе мяч, брошенный игроком с некоторой начальной скоростью под углом к горизонту, движется по параболической траектории (слайд 4).
Если начальная скорость тела при запуске с Земли равна второй космической скорости – 11,2 км/с, то тело, удаляясь от Земли, движется по параболической траектории (слайд 5).
Иногда научно-исследовательские эксперименты ученым необходимо провести в условиях невесомости. Не все могут совершить полет на космическую станцию, где состояние невесомости, как вам известно, естественно. Поэтому для достижения состояния невесомости используют полеты на специально оснащенных самолетах. В этом случае траектория движения самолета представляет собой параболу (слайд 6).
Также парабола приходила на помощь в очень тяжелых ситуациях и с её помощью одерживали победу.
В 13 веке Н.Э. Монах Бертольд Шварц открыл для европейцев порох (в Китае он был известен за много столетий до того). Это повлекло за собой революцию в военном деле – ни одна тогдашняя крепость не могла долго выдержать артиллерийский огонь.
Сначала применяли лишь настильный огонь, а это не давало возможности, например, располагать орудие за холмом, укрывая артиллеристов от выстрелов противника. Лишь после догадались применять навесной огонь, позволявший стрелять из-за укрытия, нужно было изучить движение тела, брошенного под углом к горизонту.
Первым из математиков решал эту задачу Николо Тарталья (1500-1557г), работавший в венецианском арсенале. Прозвище «Тарталья» означало «заика». Он получил это прозвище потому, что в младенчестве был ранен в лицо при взятии его родного города французами и после этого очень невнятно говорил.
Тарталья занимался многими вопросами математики и механики. Однако его не признавали университетские ученые того времени, и открытия Тартальи носят имена других математиков (формула Кардано, треугольник Паскаля).
Размышляя над движением артиллерийских снарядов, Тарталья пришел к выводу, что снаряд пролетит наибольшее расстояние, если наклонить орудие к горизонту под углом 45°. Сначала он хранил тайну этого открытия, но когда турецкий султан Сулейман Великий напал на Адриатику и Венецию, Тарталья написал герцогу Убинскому: «Так как я вижу, что волк подкрадывается к нашему стаду и что все наши пастухи готовятся к защите, то мне предоставляется предосудительным скрывать далее эти вещи, и поэтому я решил ознакомить с ними каждого истинного гражданина, чтобы каждый был лучше вооружен как для нападения, так и для защиты».
Однако он не знал еще теоретической основы законов, управляющих движением снарядов. Лишь Галилей установил законы падения тел (слайд 7). Законы падения тел, открытые Галилео-Галилеем еще в молодости, описаны только в сочинении в 1638 году. Галилей сказал: «Все знают, что брошенные горизонтально тела описывают кривые, но что эти кривые параболы, никто еще не доказал. Мы покажем все это, и наша работа послужит основанием науки, которую великие умы разработают обширнее. Сначала мы рассмотрим движения равномерные, затем естественно ускоренные и, наконец, движения стремительные, т.е. движения брошенных снарядов» (слайд 8).
Если при одной и той же скорости вылета снаряда из канала ствола орудия придавать стволу различные углы наклона к горизонту, то будут получаться различные параболы. Наибольшая дальность полета получиться при наклоне ствола, равном 45°.
Задание: прочитать п.5, выучить свойства, разобрать примеры п.5, посмотреть видеоурок, решить задания «Якласс». Учебный материал проработать в документе WORD.