В ракетно-космической технике встречаются конструкции весьма тонкой структуры, на которых размещены достаточно массивные грузы и оборудование. Это могут быть приборные отсеки в виде тонкостенных оболочек, к которым крепится различного рода оборудование, изогридные адаптеры, воспринимающие нагрузку от массивных космических аппаратов и т.п..
При конечноэлементном моделировании в этих случаях приходится иметь дело с разножесткими элементами и принципиально различающимися массовыми характеристиками.
Наглядным примером является создание КЭ моделей для описания динамики и прочности массивного приборно-агрегатного оборудования изделий и узлов его крепления. Узлы крепления, часто имеют достаточно сложную конфигурацию и для оценки их прочностных свойств требуется детализированное разбиение их на мелкие элементы. Вместе с тем их массовые характеристики имеют второстепенное влияние на динамику оборудования. При решении проблем с нагрузками и прочностью для таких конструкций инженерный опыт указывает на возможность сосредоточить массовые характеристики в центрах расположения основных грузов с сохранением их обобщенных координат и детализированным учетом жесткостных свойств узлов их подвески.
Такой подход позволит определить нагрузки на основные инерционные элементы, с использованием которых моделируется приборно-агрегатное оборудование.
Для осуществления такой процедуры собственно и разработан метод статической редукции подсистем (или статической конденсации).
Ниже дается описание этого метода.
Разрабатывается КЭ модель объекта описанного выше типа. Затем обобщенные координаты КЭ модели х и соответствующие им подматрицы масс и жесткостей разбиваются на две подгруппы: первая подгруппа обобщенных координат, в которых расположены массивные элементы, образует подвектор q; вторая, характеризующая в основном жесткостные свойства узлов крепления, образует подвектор p.
|
|
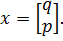
| (8.4.1) |
В соответствии с принятыми обозначениями конечноэлементные уравнения системы записываются в виде блочных векторно-матричных равенств
 =  .
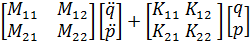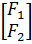| (8.4.2) |
Диссипативные члены вводятся на последующих этапах решения задачи.
Представим (8.4.2) в виде следующих блочных равенств
 ,
| (8.4.3) |
| (8.4.4) |
Второе равенство, главным образом характеризует жесткостные свойства и динамику зоны конструкции (с обобщенными координатами p), в которой отсутствуют массивные элементы и, как правило, отсутствуют внешние силы.
Поэтому в равенстве (8.4.4) допустимо пренебречь инерционными и внешними силами (определяющей для этой зоны является матрица жесткости)
 .
| (8.4.5) |
Выразим из (8.4.5) подвектор p через подвектор q
 .
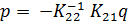| (8.4.6) |
С учетом равенства (8.4.6) соотношение для вектора обобщенных координат примет вид
 .
| (8.4.7) |
Здесь D –прямоугольная матрица
 ,
| (8.4.8) |
E - квадратная матрица, имеющая размерность вектора q,
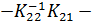прямоугольная матрица, количество строк которой совпадает с размерностью вектора p, а количество столбцов с размерностью вектора q.
Использование представления (8.4.7) позволяет в уравнении движения системы (8.4.2) сохранить только обобщенные координаты, характеризующие движение массивных элементов конструкции с учетом жесткостных свойств системы за счет статической конденсации (8.4.6) - (8.4.8).
|
|
После подстановки (8.4.7) в уравнение движения системы (8.4.2) и умножения левой и правой частей уравнения на транспонированную матрицу D T (слева) приходим к уравнению движения с существенно меньшим количеством обобщенных координат.
 .
| (8.4.9) |
Умножение левой и правой частей уравнения (8.4.2) на транспонированную матрицу D T позволяет сохранить симметрию и неотрицательность матриц масс и жесткостей уравнения (8.4.9).
Представленная здесь процедура сокращения размерности задачи при рациональном инженерном выборе сохраняемых координат q позволяет достаточно качественно описать динамику системы и называется эта процедура статической конденсацией.