Чтобы избежать численного интегрирования при определении элементов матрицы  (8.1.16), упростим вычисление обобщенных скалярных произведений
(8.1.16), упростим вычисление обобщенных скалярных произведений

| (8.2.1) |
Ниже показано, что указанные скалярные произведения могут быть выражены через реакции связей нормированных форм колебаний  . Если освободить конструкцию от интерфейсных связей и заменить их действие реакциями, то уравнения для статических решений
. Если освободить конструкцию от интерфейсных связей и заменить их действие реакциями, то уравнения для статических решений  и форм колебаний
и форм колебаний  записываются в виде (8.1.5).
записываются в виде (8.1.5).
Эти уравнения можно рассматривать как уравнения статического деформирования (L - статический оператор) одной и той же системы при различных внешних силах  и
и  .
.

| (8.2.2) |
Применяя теорему о взаимности работ Бетти [18 ] к двум системам сил (8.2.2), будем иметь
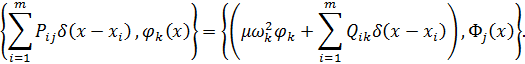
| (8.2.3) |
Учитывая правила интегрирования дельта-функций и их производных из (8.2.3) получим

| (8.2.4) |
Принимая во внимание граничные условия для кинематических параметров 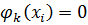 ,
, 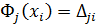 , соотношение (8.2.4) преобразуется к виду (
, соотношение (8.2.4) преобразуется к виду ( – символ Кронекера)
– символ Кронекера)
 . .
| (8.2.5) |
Отсюда получаем соотношения между коэффициентами Фурье разложения квазистатических решений и реакциями в связях, соответствующими нормированным собственным тонам колебаний закрепленных подсистем
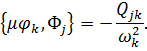
| (8.2.6) |
Отметим, что соотношение (8.2.6) имеет важное самостоятельное значение, так как оно дает возможность существенно сократить объем вычислений за счет замены интегралов или матричных операций на отношение вычисляемых в процессе решения задачи скалярных величин.
Вариант динамической редукции подсистем, используемый в зарубежных программных комплексах (метод Крейга-Бемптона)
Следует отметить, что и в методе динамической редукции с использованием квазистатики кинематического типа, и в методе Крейга-Бэмптона, и в методе построения механических аналогов лежит один и тот же физический принцип, а именно представление решения конденсируемой подсистемы в виде суммы единичных квазистатических решений и разложения по тонам колебаний закрепленной в интерфейсных точках подсистемы.
При использовании конечно-элементной постановки задачи уравнение свободной подсистемы в физических степенях свободы запишем в виде
 . .
| (8.3.1) |
Здесь M и  – матрицы масс и жесткостей свободной подсистемы,
– матрицы масс и жесткостей свободной подсистемы, 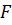 ‑ вектор внешних сил.
‑ вектор внешних сил.
Пусть число физических степеней свободы будет N
 . .
| (8.3.2) |
Будем считать последние m обобщенных координат вектора  обобщенными координатами интерфейса
обобщенными координатами интерфейса  через которые будет осуществляться стыковка данной подконструкции с основной конструкцией. Обозначим остальные
через которые будет осуществляться стыковка данной подконструкции с основной конструкцией. Обозначим остальные  обобщенные координаты вектора
обобщенные координаты вектора  через
через  .
.
Тогда вектор  (8.3.2) можно представить в блочном виде
(8.3.2) можно представить в блочном виде

| (8.3.3) |
В предположении, что подсистема кинематически возбуждается в узлах интерфейса по законам 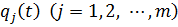 , вектор внешних сил, входящий в уравнение (8.3.1), представим в виде активных внешних сил, соответствующих подвекторам
, вектор внешних сил, входящий в уравнение (8.3.1), представим в виде активных внешних сил, соответствующих подвекторам  и
и  , и сил реакции
, и сил реакции 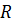 в узлах интерфейса
в узлах интерфейса

| (8.3.4) |
Решение для внеинтерфейсных обобщенных координат  ищется, как уже упоминалось, в виде комбинации m единичных квазистатических решений
ищется, как уже упоминалось, в виде комбинации m единичных квазистатических решений  и разложения по n тонам колебаний
и разложения по n тонам колебаний  закрепленной в интерфейсных координатах подсистемы
закрепленной в интерфейсных координатах подсистемы  .
.
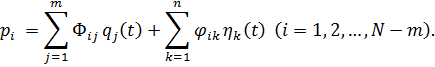
| (8.3.5) |
Здесь  – обобщенные координаты интерфейса,
– обобщенные координаты интерфейса, 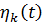 – обобщенные координаты, соответствующие тонам колебаний закрепленной в интерфейсе подсистемы.
– обобщенные координаты, соответствующие тонам колебаний закрепленной в интерфейсе подсистемы.
Равенства (8.2.5) для  являются конечноэлементными аналогами представления (8.1.2)
являются конечноэлементными аналогами представления (8.1.2)
Тогда связь между обобщенными координатами исходной конечно-элементной модели (8.3.2) и вновь введенными обобщенными координатами 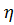 и
и  с учетом (8.3.5) запишется так
с учетом (8.3.5) запишется так
 , где , где  , ,
| (8.3.6) |

|
Матрицы форм колебаний  и статических решений
и статических решений  построим, исходя из конечно-элементной формулировки задачи (8.3.1), записанной в блочном виде с учетом представления вектора обобщенных координат
построим, исходя из конечно-элементной формулировки задачи (8.3.1), записанной в блочном виде с учетом представления вектора обобщенных координат  в виде (8.3.3)
в виде (8.3.3)
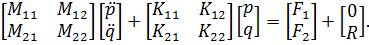
| (8.3.7) |
Отметим, что в силу симметрии матриц М и 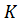 , входящих в (8.3.1), для блочных матриц, входящих в (8.3.7), справедливы равенства
, входящих в (8.3.1), для блочных матриц, входящих в (8.3.7), справедливы равенства
 . .
|
Для получения матрицы j необходимо в уравнении вектор q и, соответственно,  приравнять нулю
приравнять нулю  (то есть закрепить координаты интерфейса), положить нулю
(то есть закрепить координаты интерфейса), положить нулю 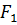 и
и 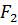 , а вектор
, а вектор  задать в виде
задать в виде 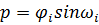 t.
t.
Тогда на основе векторного равенства для первой блочной компоненты (8.3.7) задача о собственных колебаниях, формирующих матрицу  , примет вид
, примет вид
 . .
| (8.3.8) |
После вычисления n нижних собственных тонов колебаний задачи (8.3.8) строим матрицу  , столбцами которой являются собственные вектора
, столбцами которой являются собственные вектора 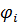 размерности
размерности  .
.
 . .
| (8.3.9) |
В итоге матрица  имеет размерность
имеет размерность  .
.
Для получения матрицы единичных статических решений  необходимо в (8.3.7) обнулить инерционные члены
необходимо в (8.3.7) обнулить инерционные члены  и внешние силы
и внешние силы  .
.
Единичные статические функции  определяются из решения следующих задач
определяются из решения следующих задач

| (8.3.10) |
Здесь  –
–  -ый столбец единичной матрицы E размерности
-ый столбец единичной матрицы E размерности  .
.
 – вектор статических реакций размерности
– вектор статических реакций размерности  в интерфейсных точках, соответствующих j -ой статической функции
в интерфейсных точках, соответствующих j -ой статической функции  .
.
Задача (8.3.10) является конечноэлементным аналогом континуальной задачи (8.1.3).
Очевидно, что сложив  векторных равенств (8.3.10) придем к матричному уравнению относительно матрицы, столбцами которой являются вектора
векторных равенств (8.3.10) придем к матричному уравнению относительно матрицы, столбцами которой являются вектора  из (8.3.10).
из (8.3.10).
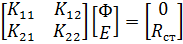 . .
| (8.3.11) |
Здесь Е – единичная матрица m -го порядка (порядок единичной матрицы совпадает с порядком вектора обобщенных координат интерфейса q), 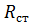 ‑ матрица статических реакций в интерфейсе, соответствующая матрице единичных статических решений
‑ матрица статических реакций в интерфейсе, соответствующая матрице единичных статических решений  .
.
Равенство (8.3.10) эквивалентно следующим двум равенствам
 . .
| (8.3.12) |
Из первого равенства (8.3.12) определяем матрицу единичных статических решений 

| (8.3.13) |
Второе равенство (8.3.12) дает возможность определить матрицу статических реакций 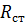 от единичных статических решений
от единичных статических решений  . После определения матриц
. После определения матриц 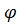 и
и  представление для
представление для  из (8.3.6) подставляем в уравнение (8.3.1) и умножаем все члены уравнения слева на
из (8.3.6) подставляем в уравнение (8.3.1) и умножаем все члены уравнения слева на  из (8.3.6)
из (8.3.6)
 ,
здесь ,
здесь  . .
| (8.3.14) |
После перемножения матриц в уравнении (8.3.14) с учетом блочной структуры матриц  и
и 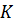 (8.3.7) будем иметь
(8.3.7) будем иметь

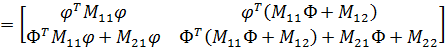 , ,
| (8.3.15) |

| (8.3.16) |
Проанализируем блочные элементы матрицы 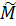 (8.3.15). Очевидно, что при единичной нормировке форм колебаний
(8.3.15). Очевидно, что при единичной нормировке форм колебаний 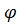 по массе
по массе
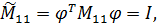 где где  – единичная матрица n- го порядка, – единичная матрица n- го порядка,
| (8.3.17) |
 , ,
| |
 . .
|
Проанализируем блочные элементы матрицы  (8.3.16). Из соотношения (8.3.8) следует матричное равенство
(8.3.16). Из соотношения (8.3.8) следует матричное равенство
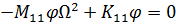 здесь здесь  . .
| (8.3.18) |
Умножая равенство (8.3.18) слева на 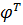 , получим
, получим

| (8.3.19) |
Очевидно, что матрица  симметрична и кроме того с учетом первого равенства (8.3.12) внедиагональные элементы матрицы
симметрична и кроме того с учетом первого равенства (8.3.12) внедиагональные элементы матрицы  равны нулю
равны нулю
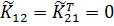 . .
| (8.3.20) |
Отметим также, что в силу равенств (8.3.12) блочный элемент матрицы (8.3.16)  равен матрице статических реакций в интерфейсе
равен матрице статических реакций в интерфейсе 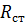 .
.
Действительно,
 . .
|
В итоге уравнение (8.3.7) приобретает следующий вид

| (8.3.21) |
Здесь  - единичная матрица, n -го порядка
- единичная матрица, n -го порядка


| (8.3.22) |
 . .
|
Следует иметь в виду, что в случае интерфейса представляющего собой узел с шестью степенями свободы (например, плоское поперечное сечение балки) матрица  равна нулю, так как в этом случае матрица
равна нулю, так как в этом случае матрица  будет характеризовать перемещения подконструкции как жесткого целого, а реакции при статическом перемещении тела в пространстве равны нулю
будет характеризовать перемещения подконструкции как жесткого целого, а реакции при статическом перемещении тела в пространстве равны нулю  .
.
Необходимо отметить, что при детализированном разбиении подконструкции на мелкие конечные элементы и при отсутствии ассоциированных с интерфейсными обобщенными координатами значительных массово-инерционных параметров определяющую роль в матрицах  и
и 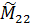 будет играть подматрица
будет играть подматрица  из (8.3.7) матрицы
из (8.3.7) матрицы  . При этом для формул (8.3.22) будут справедливы приближенные соотношения, совпадающие с (8.1.16), (8.1.17)
. При этом для формул (8.3.22) будут справедливы приближенные соотношения, совпадающие с (8.1.16), (8.1.17)
 . .
| (8.3.23) |
Cконденсированное уравнение (8.3.21) в дальнейшем обычно используется для синтезирования подсистем.