Содержание
8 Разработка методов динамического редуцирования подсистем рн с учётом действия на них активных сил.. 2
8.1 Динамическая редукция подсистем с использованием выделения квазистатики кинематического типа. 2
8.2 Определение коэффициентов Фурье разложения статических решений через реакции связей. 16
8.3 Вариант динамической редукции подсистем, используемый в зарубежных программных комплексах (метод Крейга-Бемптона) 18
8.4 Статическая редукция подсистем. 24
8.5 Синтезирование конечноэлементных моделей подконструкций для проведения анализа связанных нагрузок. 27
Разработка методов динамического редуцирования подсистем рн с учётом действия на них активных сил
В связи с развитием международных контактов в области космических исследований появилась необходимость во взаимоувязке нормативных и методических подходов Российской стороны и принятых в зарубежной практике.
При этом прежде всего возникают вопросы совместимости расчетных моделей и методик расчета нагрузок космических аппаратов и носителей, а также модулей и сегментов космических станций.
Ниже в разделе 8.1 излагаются разработанные в ЦНИИмаш методические основы динамической редукции и синтеза подсистем через интерфейс. В терминологии ЦНИИмаш этот методический подход именуется как метод выделения квазистатической составляющей кинематического типа [14].
В зарубежной практике в качестве метода динамической редукции подсистем, проводимой с целью снижения количества степеней свободы и соответственно порядка системы дифференциальных уравнений, описывающей движение конечно-элементной модели конструкции, используется метод Крейга-Бэмптона [36]. Этот метод, изложенный ниже в разделе 8.3, используется для динамической редукции в программном комплексе NASTRAN [37].
Динамическая редукция подсистем с использованием выделения квазистатики кинематического типа
Рассмотрим некоторую упругую подсистему, кинематически возбуждаемую в точках  путём задания законов их движения в некоторых направлениях
путём задания законов их движения в некоторых направлениях  во времени. Для наглядности возбуждаемую подсистему можно представить в виде пространственного упругого тела.
во времени. Для наглядности возбуждаемую подсистему можно представить в виде пространственного упругого тела.
через эти точки в последующем может осуществляться связь данной подсистемы (подконструкции) с основной системой (конструкцией).
Уравнение движения рассматриваемой подсистемы запишем в виде
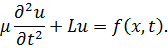
| (8.1.1) |
Здесь  – вектор перемещений,
– вектор перемещений, 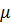 – погонная масса,
– погонная масса,  – дифференциальный оператор, характеризуюший упругие свойства подсистемы,
– дифференциальный оператор, характеризуюший упругие свойства подсистемы,  – вектор внешних активных сил.
– вектор внешних активных сил.
Будем отыскивать решение уравнения (8.1.1) в виде следующего представления

| (8.1.2) |
В (8.1.2)  – система статических решений, соответствующая единичным перемещениям интерфейса с координатами
– система статических решений, соответствующая единичным перемещениям интерфейса с координатами  в заданных направлениях
в заданных направлениях

| (8.1.3) |
Функции  по терминологии ЦНИИмаш называются квазистатическими решениями кинематического типа.
по терминологии ЦНИИмаш называются квазистатическими решениями кинематического типа.
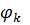 - собственные формы задачи с закрепленными точками интерфейса
- собственные формы задачи с закрепленными точками интерфейса

| (8.1.4) |
Для удобства дальнейших выкладок необходимо точки интерфейса  включить внутрь области, в которой решается уравнение (8.1.1), совместно с реакциями, вызываемыми кинематическими перемещениями
включить внутрь области, в которой решается уравнение (8.1.1), совместно с реакциями, вызываемыми кинематическими перемещениями 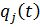 . Тогда уравнения (8.1.3) и (8.1.4), соответственно, примут вид
. Тогда уравнения (8.1.3) и (8.1.4), соответственно, примут вид

| (8.1.5) |
Здесь  - статические усилия в точках
- статические усилия в точках  , соответствующие j ‑ому статическому решению
, соответствующие j ‑ому статическому решению  из (8.1.3);
из (8.1.3);  - динамические усилия в точках
- динамические усилия в точках  , соответствующие k -ому тону колебаний
, соответствующие k -ому тону колебаний  из (8.1.4);
из (8.1.4);  - дельта-функция.
- дельта-функция.
Уравнения (8.1.5) можно трактовать как уравнения статического деформирования свободной подсистемы под действием сил реакции и инерционных сил, стоящих в правых частях.
Путём введения в уравнение (8.1.1) неизвестных реакций связей  в точках интерфейса задача о кинематическом возбуждении (8.1.1) сводится к задаче о силовом возбуждении свободной подсистемы (подконструкции). В этом случае правая часть уравнения (8.1.1) представится в виде
в точках интерфейса задача о кинематическом возбуждении (8.1.1) сводится к задаче о силовом возбуждении свободной подсистемы (подконструкции). В этом случае правая часть уравнения (8.1.1) представится в виде

| (8.1.6) |
Подставляем представление (8.1.2) в уравнение (8.1.1)

| (8.1.7) |
С учетом соотношений (8.1.5), (8.1.6) равенство (8.1.7) запишется так:


| (8.1.8) |
Умножая обе части (8.1.8) скалярно на  и учитывая ортогональность собственных форм и единичную их нормировку по массе
и учитывая ортогональность собственных форм и единичную их нормировку по массе  , получаем первую группу уравнений движения в обобщенных координатах
, получаем первую группу уравнений движения в обобщенных координатах

| (8.1.9) |
При этом все слагаемые, (обобщенные скалярные произведения по области S, занимаемой подсистемой), в которые вошла дельта-функция  обратились в нули. Очевидно, что
обратились в нули. Очевидно, что

|
Так как  по условию (8.1.4).
по условию (8.1.4).
Теперь умножим обе части равенства (8.1.8) скалярно на  .
.

 при
при  . .
| (8.1.10) |
В равенствах (8.1.10) принято во внимание соотношение
 . .
|
С учетом граничных условий для статических решений Фn (x)
 . .
|
уравнения (8.1.10) примут вид:


| (8.1.11) |
С использованием теоремы о взаимности работ Бетти [18] в следующем разделе 8.2 будет показано, что
 . .
| (8.1.12) |
Тогда вторая группа уравнений для обобщенных координат (8.1.11) с учетом (8.1.12) примет вид
 
| (8.1.13) |
Отметим, что эти уравнения по существу определяют реакции в связях (в интерфейсе) через обобщенные координаты и их производные.
Сгруппируем уравнения (8.1.9) и (8.1.13), сделав в них перестановку слагаемых

| (8.1.14) |
Отметим, что в уравнениях (8.1.11)-(8.1.14) и далее в разделе 8.2 под  ,
,  и
и 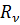 понимаются усилия по n -ой обобщенной координате интерфейса, соответствующие перемещению
понимаются усилия по n -ой обобщенной координате интерфейса, соответствующие перемещению 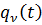 для j -ого статического решения
для j -ого статического решения  , k ‑ой формы колебаний
, k ‑ой формы колебаний  и общей реакции в интерфейсе на подсистему, соответственно.
и общей реакции в интерфейсе на подсистему, соответственно.
Запишем уравнения (8.1.14) в матричной форме
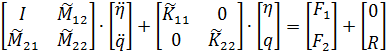 . .
| (8.1.15) |
Значения матриц, входящих в (8.1.15), представлены ниже.
 – единичная матрица порядка
– единичная матрица порядка  .
.
Элементы прямоугольной матрицы  порядка
порядка 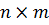 имеют вид
имеют вид

| (8.1.16) |
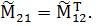
|
Элементы квадратной матрицы  порядка
порядка  имеют вид
имеют вид

| (8.1.17) |
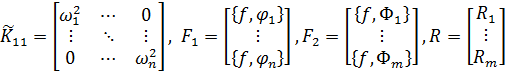 . .
| (8.1.18) |
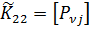 – квадратная матрица порядка
– квадратная матрица порядка  .
.
Верхний индекс "Т" означает транспонирование матриц или векторов.
Отметим, что при определении элементов матрицы  с целью сокращения объема вычислений (за счет исключения операций интегрирования) следует пользоваться равенствами (8.1.12).
с целью сокращения объема вычислений (за счет исключения операций интегрирования) следует пользоваться равенствами (8.1.12).
Отметим, что в случае пространственного упругого тела перемещения  (8.1.2), статические решения
(8.1.2), статические решения 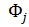 (8.1.3) и формы колебаний
(8.1.3) и формы колебаний  (8.1.4) являются трехмерными векторами, каждая из компонент которых отражает перемещения в соответствующих направлениях
(8.1.4) являются трехмерными векторами, каждая из компонент которых отражает перемещения в соответствующих направлениях

| (8.1.19) |
Погонная масса или плотность m при этом является скалярной функцией, зависящей от координат подсистемы.
Под обобщенными скалярными произведениями в (8.1.9)-(8.1.18) для пространственной упругой подсистемы понимаются следующие объемные интегралы

| (8.1.20) |

| |

|
Нормировка форм колебаний по единичной массе осуществляется так:

|
Остановимся на случае динамической конденсации подсистемы с интерфейсом, представляющим собой один узел (плоское сечение) с шестью степенями свободы. При этом роль статических функций выполняют единичные перемещения системы, как твердого целого. Такой случай достаточно типичен при синтезировании РН и космических аппаратов, где в качестве интерфейса служит плоское балочное сечение РН или адаптера с шестью степенями свободы.
В этом случае роль обобщенных координат играют векторы линейных и малых угловых перемещений  ,
,  интерфейса, заданных в системе координат 0,
интерфейса, заданных в системе координат 0,  связанной с интерфейсом
связанной с интерфейсом

| (8.1.21) |
Полный вектор обобщенных координат интерфейса обозначим так
 . .
| (8.1.22) |
Каждая компонента вектора (8.1.22) зависит от времени.
Тогда вектор перемещений  любого узла подсистемы как твердого целого с координатами
любого узла подсистемы как твердого целого с координатами  определяется следующим образом:
определяется следующим образом:
 . .
| (8.1.23) |
Здесь второе слагаемое является векторным произведением

 , , 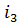 – единичные орты. – единичные орты.
|
Отметим, что формула для перемещений при линейной постановке задачи (при малых перемещениях) совпадает по структуре с формулой для скоростей.
Для удобства дальнейших преобразований в качестве подсистемы будет рассматриваться континуальное трехмерное упругое тело.
С учетом принятых обозначений (8.1.21), (8.1.22) и соотношения (8.1.21) нетрудно убедиться, что представление (8.1.2) преобразуется в следующее

| (8.1.24) |
В представлении (8.1.24) первая сумма характеризует движение подсистемы как твердого целого при кинематическом возбуждении обобщенных координат интерфейса (8.1.22). Вектора  являются столбцами приведенной ниже матрицы Ψ
являются столбцами приведенной ниже матрицы Ψ

 . .
| (8.1.25) |
Во вторую сумму (8.1.24) входят собственные формы колебаний  , консольно закрепленной в интерфейсе подсистемы. В случае подсистемы в виде пространственного упругого тела перемещения всех точек этого тела, находящихся в интерфейсной плоскости, равны нулю.
, консольно закрепленной в интерфейсе подсистемы. В случае подсистемы в виде пространственного упругого тела перемещения всех точек этого тела, находящихся в интерфейсной плоскости, равны нулю.
Отметим, что все соотношения (8.1.15)-(8.1.18), полученные для m интерфейсных обобщенных координат, остаются справедливыми и для интерфейса в виде плоского сечения с шестью степенями свободы (8.1.22). При этом статические решения (8.1.3) во всех соотношениях (8.1.15)-(8.1.18) заменяются векторами  ,
, 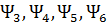 , являющимися столбцами матрицы (8.1.25), которые характеризуют движение подсистемы как твердого целого (будем далее именовать их условно твердыми тонами).
, являющимися столбцами матрицы (8.1.25), которые характеризуют движение подсистемы как твердого целого (будем далее именовать их условно твердыми тонами).
Необходимо также иметь в виду, что при динамической конденсации подсистемы к интерфейсу, представляющему собой плоское сечение с шестью степенями свободы, матрица  , так как усилия в интерфейсе при перемещении стыкуемой подсистемы как жесткого целого равны нулю (
, так как усилия в интерфейсе при перемещении стыкуемой подсистемы как жесткого целого равны нулю ( .
.
Остановимся на анализе структуры матрицы 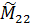 , элементы которой с учетом (8.1.15), (8.1.17) и (8.1.25) определяются так:
, элементы которой с учетом (8.1.15), (8.1.17) и (8.1.25) определяются так:

| (8.1.26) |
Легко убедиться, что матрица 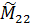 с учетом (8.1.25) и (8.1.26) превращается в массово-инерционный тензор подсистемы как твердого тела.
с учетом (8.1.25) и (8.1.26) превращается в массово-инерционный тензор подсистемы как твердого тела.

| (8.1.27) |
Матрица 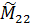 является симметричной (здесь показана верхняя треугольная подматрица).
является симметричной (здесь показана верхняя треугольная подматрица).
Элементами матрицы 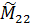 являются массы, моменты инерции и статические моменты подсистемы (
являются массы, моменты инерции и статические моменты подсистемы ( – масса подсистемы,
– масса подсистемы, 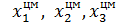 – координаты центра масса,
– координаты центра масса,  моменты инерции).
моменты инерции).
Отметим, что в данном случае погонные массы (или плотности) вдоль трех осей одинаковы, поэтому суммарные массы вдоль трех осей также будут одинаковыми и равными физической массе  .
.
Для иллюстрации продемонстрируем получение отдельных элементов  матрицы
матрицы 
С учетом (8.1.25) и (8.1.26) будем иметь
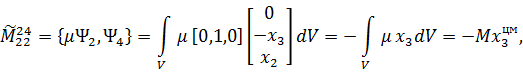


| (8.1.28) |
Здесь в подинтегральных выражениях учтено матричное равенство для скалярных произведений  .
.
Проанализируем структуру матрицы  В соответствии с (8.1.16), для варианта одного плоского интерфейса с шестью степенями свободы эта матрица выглядит так:
В соответствии с (8.1.16), для варианта одного плоского интерфейса с шестью степенями свободы эта матрица выглядит так:
 . .
| (8.1.29) |
Из структуры столбцов матрицы  видно, что они являются коэффициентами Фурье-разложения векторов
видно, что они являются коэффициентами Фурье-разложения векторов 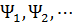 ,
,  , характеризующих движение подсистемы как твердого целого.
, характеризующих движение подсистемы как твердого целого.
В самом деле, представим некоторый вектор  его разложением по собственным формам колебаний консольно закрепленной подсистемы.
его разложением по собственным формам колебаний консольно закрепленной подсистемы.

| (8.1.30) |
Известно, что собственные формы колебаний упругих систем представляют собой полную систему функций и собственные формы, отвечающие различным собственным числам, ортогональны с весовой функцией в виде погонной массы (или плотности). Для удобства формы колебаний будем считать нормированными по массе 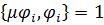 .
.
Умножая левую и правую части (8.1.30) скалярно на  , получим
, получим
 . .
| (8.1.31) |
С учетом (8.1.31) равенство (8.1.30) перепишется в виде
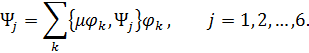
| (8.1.32) |
Умножим левую и правую часть равенства (8.1.32) на погонную массу 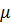
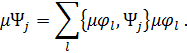
| (8.1.33) |
Перемножим скалярно (обобщенное скалярное умножение) левые и правые части равенств (8.1.32) и (8.1.33)

| (8.1.34) |
в силу ортогональности собственных форм колебаний в правой части (8.1.34) останутся только те слагаемые, в которых k=l, и правая часть превратится в однократную сумму
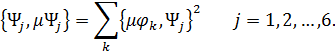
| (8.1.35) |
Очевидно, что слева в равенстве (8.1.35) стоят диагональные элементы матрицы 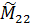 (8.1.26), (8.1.27), то есть, диагональные элементы тензора инерции.
(8.1.26), (8.1.27), то есть, диагональные элементы тензора инерции.
Для рассматриваемой подконструкции в виде трехмерного упругого тела с одинаковыми погонными массами (или плотностями) во всех направлениях левая часть равенства (8.1.35) при j =1,2,3 равна одной и той же величине – физической массе  (см. матрицу (8.1.27)).
(см. матрицу (8.1.27)).
Однако правые части (8.1.35) при j =1,2,3 являются различными!!!
Чем это объяснить?
Объяснение содержится в степени сходимости рядов (8.1.32) по тонам колебаний. При бесконечном количестве членов ряда сходимость рядов в среднем обеспечивается. Однако при ограниченном количестве тонов колебаний для разных векторов 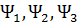 будет достигнута различная степень сходимости и правые части равенств (8.1.35) при
будет достигнута различная степень сходимости и правые части равенств (8.1.35) при 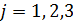 могут различаться.
могут различаться.
Эффект различия сходимости правых частей в (8.1.35) при 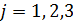 наиболее легко объяснить на примере динамической конденсации подсистемы, представляющей собой прямолинейную металлическую балку с распадающимися продольными и поперечными тонами колебаний. В этом случае вектор
наиболее легко объяснить на примере динамической конденсации подсистемы, представляющей собой прямолинейную металлическую балку с распадающимися продольными и поперечными тонами колебаний. В этом случае вектор  (если ось
(если ось  направлена вдоль оси стержня) будет характеризовать единичное перемещение балки вдоль оси
направлена вдоль оси стержня) будет характеризовать единичное перемещение балки вдоль оси  ), функции
), функции  и
и  – единичные перемещения балки в поперечных направлениях. При этом в соотношении (8.1.32) единичный продольный вектор будет разлагаться по чисто продольным тонам колебаний, а единичные поперечные вектора – по чисто поперечным тонам колебаний. Вместе с тем продольные и поперечные тона колебаний образуют общий базис при конденсации балочной подсистемы. Причем количество учитываемых тонов при динамической конденсации задается, как правило, путем ограничения верхнего частотного диапазона f sup. В этом частотном диапазоне поперечных тонов обычно присутствует больше чем продольных и сходимость рядов (8.1.32) будет различаться, хотя в пределе при стремлении количества членов рядов (8.1.32) к бесконечности правые части равенства (8.1.35) при
– единичные перемещения балки в поперечных направлениях. При этом в соотношении (8.1.32) единичный продольный вектор будет разлагаться по чисто продольным тонам колебаний, а единичные поперечные вектора – по чисто поперечным тонам колебаний. Вместе с тем продольные и поперечные тона колебаний образуют общий базис при конденсации балочной подсистемы. Причем количество учитываемых тонов при динамической конденсации задается, как правило, путем ограничения верхнего частотного диапазона f sup. В этом частотном диапазоне поперечных тонов обычно присутствует больше чем продольных и сходимость рядов (8.1.32) будет различаться, хотя в пределе при стремлении количества членов рядов (8.1.32) к бесконечности правые части равенства (8.1.35) при 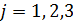 будут стремиться к одной и той же величине – физической массе подсистемы
будут стремиться к одной и той же величине – физической массе подсистемы  .
.
В связи со сказанным одними из критериев адекватности редуцированной модели исходной КЭ модели является степень выполнения равенств (8.1.35). Это означает, что для создания качественной модели при динамической конденсации подсистемы количество учитываемых тонов закрепленной в интерфейсе подсистемы должно обеспечить сходимость по массовым и инерционным параметрам. В зарубежных комплексах это требование формулируется как "сходимость эффективных масс".
По существу, соотношения (8.1.35) являются обобщением равенства Парсеваля-Бесселя [///] применительно к механическим подсистемам.
Опыт показывает, что при редуцировании КЭ моделей космических аппаратов для синтезирования их с РН обычно используется частотный диапазон до 100 Гц. При этом эффективные массы, как правило, превышают 90% их физических значений.
Если же сходимость эффективных масс в частотном диапазоне до 100 Гц недостаточна, частотный диапазон увеличивают для обеспечения удовлетворительной сходимости.
Очевидным является также второе требование для обеспечения кондиционности редуцированной модели. Оно заключается в следующем – частотный диапазон, который используется для динамической редукции, должен в 1.5-2 раза превышать частотный диапазон внешних воздействий.
Необходимо также отметить, что при редуцировании подсистемы с интерфейсом в виде плоского сечения с шестью степенями свободы правая часть соотношения (8.1.35) формируется напрямую из матрицы  (8.1.29) как сумма квадратов элементов столбцов.
(8.1.29) как сумма квадратов элементов столбцов.
В общем случае при использовании интерфейсов с произвольным количеством степеней свободы (и, соответственно, использовании единичных статических решений (8.1.3)) в явном виде не присутствуют в матрицах  коэффициенты Фурье-разложения векторов, характеризующих движение подсистемы как твердого целого.
коэффициенты Фурье-разложения векторов, характеризующих движение подсистемы как твердого целого.
Вместе с тем оценка достаточного количества собственных тонов колебаний подсистемы для динамической редукции проводится по сходимости эффективных масс, то есть по степени выполнения равенств (8.1.35).
Причина этого заключается в особенностях совокупности единичных статических решений, используемых в представлении (8.1.2).
Для этого необходимо сложить отдельные группы статических решений типа (8.1.3), интерфейсные обобщенные координаты которых принимают единичные значения по перемещениям и углам поворота в соответствии с векторами 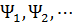 ,
,  .
.
Например, сложим k 1 статических решений  с единичными перемещениями интерфейсных координат в направлении вектора
с единичными перемещениями интерфейсных координат в направлении вектора  (в направлении оси
(в направлении оси  ).
).
 или или  , ,
| (8.1.36) |
где 
При этом сумма функций  должна удовлетворять сумме граничных условий (8.1.3), а именно
должна удовлетворять сумме граничных условий (8.1.3), а именно
 . .
| (8.1.37) |
Очевидно, что функция  , удовлетворяющая уравнению (8.1.36) и граничным условиям (8.1.37), описывает единичное перемещение подсистемы в направлении
, удовлетворяющая уравнению (8.1.36) и граничным условиям (8.1.37), описывает единичное перемещение подсистемы в направлении  , то есть
, то есть
 . .
| (8.1.38) |
В связи с тем, что сумма статических решений по любой из координат представляет собой единичное смещение или единичный угол поворота подсистемы как жесткого целого, проверяется сходимость квадратов коэффициентов Фурье не отдельных статических решений, а соответствующей суммы (8.1.38), то есть сходимость эффективных масс (8.1.35).
Кроме того, следует иметь в виду, что базис собственных функций, по которым разлагаются статические решения и тона твердого тела, образован собственными формами колебаний закрепленной в интерфейсных точках подсистемы, то есть формы колебаний в интерфейсных точках равны нулю. Отсюда следует, что разложение по полученному таким образом базису функций отличных от нуля в интерфейсных точках (а это имеет место для тонов твердого тела) будет хуже сходиться, чем обобщенные ряды Фурье статических функций, каждая из которых отличается от нуля только в одной точке интерфейса.
Поэтому считается, что, если при используемом базисе собственных функций (закрепленной в интерфейсных точках подсистемы) достигается выполнение равенств (8.1.35) для тонов твердого тела, то это обеспечивает удовлетворительный результат для любого количества интерфейсных точек (и, соответственно, любого количества статических функций).
В связи с этим критерий сходимости эффективных масс используется при динамической конденсации подсистем с любым количеством обобщенных интерфейсных координат.