Распределение Коши
Распределение Коши – это экзотическое распределение часто употребляют с иллюстративной целью вследствие его необычного свойства: дисперсия распределения Коши оказывается бесконечной.
Отличительной особенностью распределения Коши являются очень тяжелые хвосты. В частности, не существует ни один из моментов этого распределения, даже математическое ожидание.
| Область x | -Ґ < x < Ґ |
| Параметры | x0 - параметр расположения; h - парамерт масштаба |
| Плотность (функция вероятности) | 
|
| Математическое ожидание | Не существует |
| Дисперсия | Не существует |
График f(x) при x0 = 10, h = 0.8
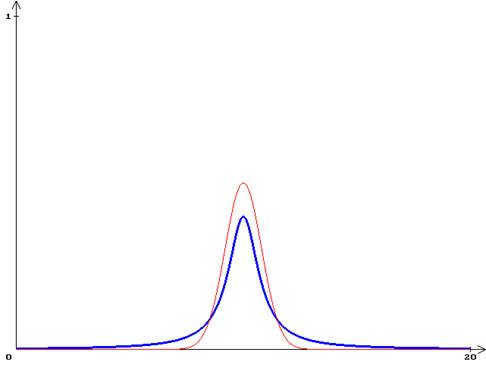
Пример распределения Коши
Предположим, что имеется программа, которая вводит массив, затем его сортирует методом простого выбора, а после этого выводит. При этом число элементов в массиве произвольно (условимся, что оно подчинено равномерному распределению). Тогда быстрота работы программы будет подчиняться распределению Коши.
Доказательство
Пусть n - количество элементов в массиве. При вводе и выводе массива потребуется по n "тяжеловесных" по времени операций (ввод и вывод). На этапе сортировки производится сравнение каждого элемента кроме последнего со всеми остальными (следует заметить, что алгоритм можно улучшить, если не "пробегать" по уже отсортированной части), т. е. имеем еще (n - 1)(n - 1) "тяжеловесных" по времени операций. В итоге получаем n2 - 2n + 1 + 2n = n2 + 1 "задержек" времени. Так как быстрота работы программы является величиной, обратно пропорциональной времени, то в итоге получим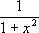 
. Если закрыть глаза на отсутствие p, то последняя формула соответствует формуле плотности для распределения Коши при нулевом параметре расположения и единичном параметре масштаба.
Рассмотрим пример, где предположим, что артиллерийское орудие расположено на единичном расстоянии от сколь угодно длинной стены. Лафет орудия вращается с постоянной скоростью. Изобразим это условно на рисунке 1.
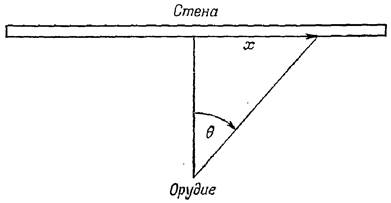
Рисунок 1 – Орудие
На каждом обороте в случайный момент времени из орудия производится выстрел. Вычислим, как при этом будут распределены попадания по стене.
Обозначим через букву θ угол, на который повернулся ствол орудия относительно начального положения (по нормали к стене), а через букву χ – расстояние вдоль стены от ее середины до точки попадания. Снаряд попадет в стену только при условии, что θ заключено в пределах от –π/2 до +π/2. В силу того что все значения углов равновероятны, для величины θ используется равномерное распределение:
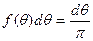, (1)
при условии, что: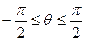 
.
Поскольку:
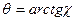, (2)
то: 
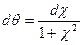(3)
Таким образом, плотность распределения величины χ равна:
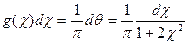, (4)
при условии, что: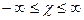 
.
Эта функция изображена на рисунке 2. Видно, что эта функция симметрична относительно нуля, и ее среднее значение поэтому равно нулю.
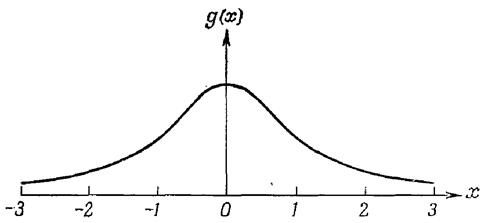
Рисунок 2 – Функция плотности распределения
Доказать это можно с помощью обычного выражения:
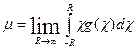(4)
Из этого следует, что:
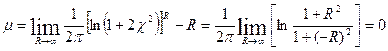(5)
Тогда дисперсия такого распределения будет:
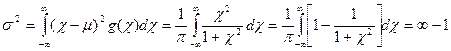(6)
Следовательно, что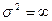 
.
Пусть некая общая теорема доказана в предположении, что рассматриваемая величина обладает конечной дисперсией. Если эта теорема окажется несправедливой для распределения Коши, то это будет означать,
что сделанное предположение необходимо.
Математическое ожидание и дисперсия случайной величины
Дискретное распределение вероятности случайной величины χ полностью задается множеством значений вероятности или функцией распределения. Непрерывное распределение полностью задается его плотностью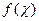 
. Во многих случаях бывает необходимо выделить наиболее важные свойства распределения. Для этого используются такие характеристики, как среднее значение, дисперсия, асимметрия и другие.
Математическое ожидание случайной величины χ – есть среднее значение χ с учетом вероятности (или плотности вероятности) осуществления каждого значения χ.
Для дискретного распределения вычисляется по формуле 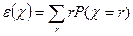(7):
(7)
Для непрерывного распределения вычисляется по формуле 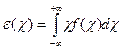(8):
(8)
Принято обозначать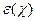 
через μ – так что в дальнейшем будем использовать эту величину как характеристику положения распределения χ.
Так же, есть другое определение математического ожидания: математическое ожидание функции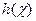 
случайной величины χ есть средняя величина 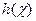по всем возможным значениям переменной χ, то есть:
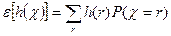, (9)
или
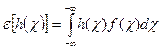. (10)
Асимметрия
Асимметрия характеризуется параметром:
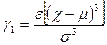(11)
Асимметрия отрицательна, если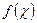 
сильно вытянуто влево от μ, и положительна, если 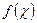вытянуто вправо от μ.Если распределение симметрично, то параметр γ1 равен нулю.
Дисперсия
При предположении, что формула (12) верна:
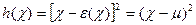(12)
получим, что дисперсия χ равна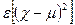 
.
Общепринято, что обозначается она через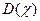 
или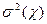 
. Корень квадратный из этой величины σ называют среднеквадратичным или стандартным отклонением χ и используют как меру разброса χ относительно среднего значения μ.
Метод Коши
Пусть в точке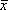 
требуется определить направление наискорейшего спуска (то есть направление наибольшего локального уменьшения f(x)). Разложим f(x) в ряд Тейлора в окрестности точки и отбросим члены второго порядка по 
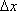и выше.
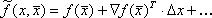
Локальное уменьшение f(x) определяется вторым слагаемым, то есть наибольшее уменьшение f(x) будет тогда, когда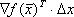 
будет иметь наибольшую отрицательную величину. Этого можно добиться выбором S(k): 
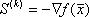, тогда второе слагаемое примет вид: 
.
Этот случай соответствует наискорейшему локальному спуску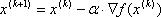 
.
Недостатки:
· остаётся вопрос выбора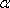 
;
· вблизи точки минимума медленно сходится, так как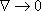 
.
будем находить путём минимизации функции f(x(k+1)) в направлении.
Метод обладает большой надёжностью но медленную сходимость вблизи точки минимума устранить нельзя. Поэтому метод самостоятельно обычно не используется, а используется как предварительная процедура для более сложных методов.
Достоинсиво:
на каждой итерации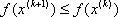 
- выполняется свойство убывания функции на каждой итерации.
Алгоритм метода.
1) Задать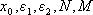 
- начальное приближение, параметр окончания работы алгоритма Коши, параметр окончания работы одномерного алгоритма, количество переменных и максимальное количество итераций соответственно.
2) Вычислить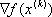 
3) Если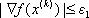 
, то xk=x* иначе, если 
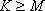, то xk=x*. Перейти к п. 4.
4) Решить задачу минимизации функции f(x(k+1)) и найти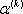 
используя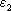 
5) Вычислить следующее приближение по формуле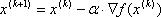
6) Если, то xk =x* иначе k=k+1 и перейти к п. 2.
Формулы Коши.
Если f(z) аналитическая в области D и непрерывная в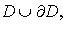 
где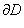 
- граница области D, то имеют место:
1) интегральная теорема Коши:
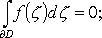
2) интегральная формула Коши:
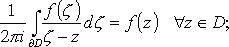
3) интегральное представление для производных:
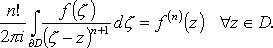
Степенные ряды
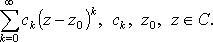
Радиус сходимости степенного ряда (формула Коши-Адамара),
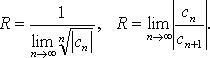
Круг сходимости:
3.Практическая часть
3.1 Получение 1000 возможных значений случайных величин X и Y, распределенных по закону Коши.
| X | (X-MX)^2 | (X-MX)^3 | (X-MX)^4 | Y | (Y-MY)^2 | (Y-MY)^3 | (Y-MY)^4 | |||
| 1,6003 | 0,36036 | 0,216324 | 0,129859 | -0,3443 | 11,18434 | -37,4038 | 125,0895 | |||
| 1,3764 | 0,141677 | 0,053327 | 0,020072 | 1,1504 | 3,42102 | -6,32752 | 11,70338 | |||
| 2,4751 | 2,17592 | 3,2097 | 4,734628 | 1,804 | 1,430416 | -1,71078 | 2,04609 | |||
| 1,0355 | 0,00126 | 4,47E-05 | 1,59E-06 | 1,6003 | 1,95916 | -2,74224 | 3,838308 | |||
| 0,5543 | 0,198648 | -0,08854 | 0,039461 | -2,6051 | 31,41715 | -176,096 | 987,0371 | |||
| -0,7813 | 3,17303 | -5,65212 | 10,06812 | 2,7475 | 0,063756 | -0,0161 | 0,004065 | |||
| -0,0875 | 1,182656 | -1,28614 | 1,398676 | -1,1918 | 17,57119 | -73,6549 | 308,7466 | |||
| -0,6009 | 2,562881 | -4,10292 | 6,568358 | -0,5095 | 12,31659 | -43,2251 | 151,6984 | |||
| -1,5399 | 6,451092 | -16,3851 | 41,61659 | -0,5317 | 12,4729 | -44,0506 | 155,5734 | |||
| -0,3249 | 1,75536 | -2,32568 | 3,081289 | -5,4608 | 71,58514 | -605,668 | 5124,432 | |||
| -1,5399 | 6,451092 | -16,3851 | 41,61659 | 0,3249 | 7,15616 | -19,1434 | 51,21063 | |||
| -0,8391 | 3,382289 | -6,22037 | 11,43988 | 4,3315 | 1,772892 | 2,360606 | 3,143147 | |||
| -1,1106 | 4,454632 | -9,40195 | 19,84375 | 0,5095 | 6,20259 | -15,4476 | 38,47213 | |||
| -1,2799 | 5,197944 | -11,8508 | 27,01862 | -0,0699 | 9,424286 | -28,9316 | 88,81717 | |||
| 2,7475 | 3,053756 | 5,336439 | 9,325427 | -0,8098 | 14,51458 | -55,2976 | 210,6729 | |||
| 0,0175 | 0,965306 | -0,94841 | 0,931816 | -1,4227 | 19,56028 | -86,5092 | 382,6044 | |||
| -0,1228 | 1,26068 | -1,41549 | 1,589314 | 2,6051 | 0,155946 | -0,06158 | 0,024319 | |||
| 0,2309 | 0,591515 | -0,45493 | 0,34989 | 1,2799 | 2,958744 | -5,08934 | 8,754166 | |||
| 0,0175 | 0,965306 | -0,94841 | 0,931816 | 0,4452 | 6,527003 | -16,6752 | 42,60177 | |||
| 0,3249 | 0,45576 | -0,30768 | 0,207717 | -0,2493 | 10,55795 | -34,3059 | 111,4703 | |||
| -3,7321 | 22,39277 | -105,965 | 501,4362 | -1,0355 | 16,28526 | -65,7192 | 265,2097 | |||
| 0,7536 | 0,060713 | -0,01496 | 0,003686 | 3,2709 | 0,073387 | 0,01988 | 0,005386 | |||
| -7,1154 | 65,85972 | -534,478 | 4337,502 | 9,5144 | 42,43741 | 276,4542 | 1800,934 | |||
| 0,1584 | 0,708291 | -0,5961 | 0,501676 | 0,9657 | 4,138376 | -8,4187 | 17,12616 | |||
| -5,1446 | 37,75611 | -231,996 | 1425,524 | 0,9004 | 4,40832 | -9,25571 | 19,43329 | |||
| 3,4874 | 6,187159 | 15,38994 | 38,28093 | -0,9325 | 15,46456 | -60,8144 | 239,1525 | |||
| -0,8693 | 3,494282 | -6,53186 | 12,21001 | 1,1918 | 3,269587 | -5,91207 | 10,6902 | |||
| -2,246 | 10,53652 | -34,2015 | 111,0182 | 1,3764 | 2,636077 | -4,27993 | 6,948902 | |||
| 1,7321 | 0,53597 | 0,392384 | 0,287264 | 0,2309 | 7,667915 | -21,2332 | 58,79692 | |||
| -0,8098 | 3,275376 | -5,92778 | 10,72809 | 1,1106 | 3,569832 | -6,74484 | 12,7437 | |||
| 1,8807 | 0,775632 | 0,6831 | 0,601606 | 0,0875 | 8,482656 | -24,7057 | 71,95546 | |||
| -0,5095 | 2,27859 | -3,43953 | 5,191974 | 0,9004 | 4,40832 | -9,25571 | 19,43329 | |||
| 0,0175 | 0,965306 | -0,94841 | 0,931816 | 9,5144 | 42,43741 | 276,4542 | 1800,934 | |||
| -0,4245 | 2,0292 | -2,8906 | 4,117654 | 8,1443 | 26,46382 | 136,1378 | 700,3339 | |||
| 1,1504 | 0,02262 | 0,003402 | 0,000512 | -8,1443 | 124,1954 | -1384,07 | 15424,5 | |||
| 1,2349 | 0,055178 | 0,012961 | 0,003045 | 0,4663 | 6,419636 | -16,2654 | 41,21172 | |||
| -0,1763 | 1,383682 | -1,62762 | 1,914575 | 9,5144 | 42,43741 | 276,4542 | 1800,934 | |||
| -0,4877 | 2,213251 | -3,29265 | 4,898481 | -0,5543 | 12,63305 | -44,9016 | 159,5939 | |||
| -2,4751 | 12,07632 | -41,9664 | 145,8375 | -1,6643 | 21,75569 | -101,475 | 473,3102 | |||
| -0,0699 | 1,144686 | -1,2247 | 1,310306 | -0,2493 | 10,55795 | -34,3059 | 111,4703 | |||
| 1,7321 | 0,53597 | 0,392384 | 0,287264 | -0,3443 | 11,18434 | -37,4038 | 125,0895 | |||
| 2,4751 | 2,17592 | 3,2097 | 4,734628 | 2,1445 | 0,73188 | -0,62612 | 0,535649 | |||
| -0,5095 | 2,27859 | -3,43953 | 5,191974 | 1,5399 | 2,131892 | -3,11278 | 4,544964 | |||
| 0,3443 | 0,429942 | -0,28191 | 0,184851 | 0,1763 | 7,973282 | -22,5142 | 63,57322 | |||
| -0,6745 | 2,80395 | -4,69521 | 7,862137 | -0,7002 | 13,69148 | -50,6612 | 187,4566 | |||
| 0,5774 | 0,178591 | -0,07547 | 0,031895 | -0,0699 | 9,424286 | -28,9316 | 88,81717 | |||
| 4,3315 | 11,09889 | 36,97596 | 123,1854 | 1,6643 | 1,784094 | -2,38302 | 3,182993 | |||
| 0,7265 | 0,074802 | -0,02046 | 0,005595 | -0,0875 | 9,532656 | -29,4321 | 90,87154 | |||
| 0,7002 | 0,08988 | -0,02695 | 0,008078 | 0,3057 | 7,259252 | -19,5586 | 52,69675 | |||
| 0,9004 | 0,00992 | -0,00099 | 9,84E-05 | -0,6494 | 13,31812 | -48,6031 | 177,3723 | |||
| -0,0875 | 1,182656 | -1,28614 | 1,398676 | 2,246 | 0,568516 | -0,42866 | 0,32321 | |||
| 0,2679 | 0,53597 | -0,39238 | 0,287264 | -0,4877 | 12,16405 | -42,4246 | 147,9641 | |||
| -3,7321 | 22,39277 | -105,965 | 501,4362 | 1,5399 | 2,131892 | -3,11278 | 4,544964 | |||
| 0,7265 | 0,074802 | -0,02046 | 0,005595 | 2,1445 | 0,73188 | -0,62612 | 0,535649 | |||
| 0,2126 | 0,619999 | -0,48819 | 0,384398 | -1,3764 | 19,15288 | -83,8207 | 366,8327 | |||
| -1,0355 | 4,14326 | -8,43361 | 17,16661 | 0,5095 | 6,20259 | -15,4476 | 38,47213 | |||
| 0,2867 | 0,508797 | -0,36292 | 0,258874 | -0,0875 | 9,532656 | -29,4321 | 90,87154 | |||
| 0,7536 | 0,060713 | -0,01496 | 0,003686 | 0,8391 | 4,669489 | -10,0903 | 21,80413 | |||
| -9,5307 | 110,8956 | -1167,81 | 12297,84 | -0,4245 | 11,7272 | -40,1598 | 137,5272 | |||
| 0,8321 | 0,02819 | -0,00473 | 0,000795 | 1,0724 | 3,715642 | -7,16227 | 13,80599 | |||
| -5,6713 | 44,50624 | -296,915 | 1980,806 | 0,2867 | 7,361997 | -19,9753 | 54,199 | |||
| -0,1228 | 1,26068 | -1,41549 | 1,589314 | -0,2309 | 10,43871 | -33,7264 | 108,9668 | |||
| -2,1445 | 9,88788 | -31,0924 | 97,77018 | -0,0349 | 9,210618 | -27,9533 | 84,83548 | |||
| 0,6494 | 0,12292 | -0,0431 | 0,015109 | -0,6494 | 13,31812 | -48,6031 | 177,3723 | |||
| -0,7002 | 2,89068 | -4,91473 | 8,356031 | -0,1763 | 10,08888 | -32,0453 | 101,7855 | |||
| 3,2709 | 5,156987 | 11,711 | 26,59451 | 0,1763 | 7,973282 | -22,5142 | 63,57322 | |||
| 0,2679 | 0,53597 | -0,39238 | 0,287264 | 0,2307 | 7,669022 | -21,2378 | 58,81391 | |||
| 0,9004 | 0,00992 | -0,00099 | 9,84E-05 | -1,3764 | 19,15288 | -83,8207 | 366,8327 | |||
| 1,5399 | 0,291492 | 0,157377 | 0,084968 | -0,5095 | 12,31659 | -43,2251 | 151,6984 | |||
| 0,1584 | 0,708291 | -0,5961 | 0,501676 | 6,3138 | 10,98127 | 36,38973 | 120,5883 | |||
| -0,6249 | 2,6403 | -4,29022 | 6,971184 | -1,0355 | 16,28526 | -65,7192 | 265,2097 | |||
| -1,804 | 7,862416 | -22,0462 | 61,81759 | 0,1763 | 7,973282 | -22,5142 | 63,57322 | |||
| -0,9325 | 3,734556 | -7,21703 | 13,94691 | 4,1108 | 1,233877 | 1,37059 | 1,522452 | |||
| 1,4281 | 0,18327 | 0,078458 | 0,033588 | -0,7265 | 13,8868 | -51,7492 | 192,8433 | |||
| 1,4281 | 0,18327 | 0,078458 | 0,033588 | -0,2309 | 10,43871 | -33,7264 | 108,9668 | |||
| 0,2493 | 0,56355 | -0,42306 | 0,317589 | -6,8138 | 96,31067 | -945,174 | 9275,745 | |||
| -2,3559 | 11,26206 | -37,7944 | 126,8341 | 1,6643 | 1,784094 | -2,38302 | 3,182993 | |||
| 0,7813 | 0,04783 | -0,01046 | 0,002288 | -0,1051 | 9,641646 | -29,9383 | 92,96134 | |||
| 0,02126 | 0,957932 | -0,93757 | 0,917634 | 0,2493 | 7,56635 | -20,8128 | 57,24966 | |||
| 0,5774 | 0,178591 | -0,07547 | 0,031895 | 0,0524 | 8,688346 | -25,6098 | 75,48735 | |||
| -11,4301 | 154,5074 | -1920,54 | 23872,53 | 3,4874 | 0,237559 | 0,115786 | 0,056434 | |||
| -0,0349 | 1,071018 | -1,1084 | 1,14708 | -4,1108 | 50,56348 | -359,547 | 2556,665 | |||
| 2,7475 | 3,053756 | 5,336439 | 9,325427 | 0,3057 | 7,259252 | -19,5586 | 52,69675 | |||
| 1,0355 | 0,00126 | 4,47E-05 | 1,59E-06 | 1,4281 | 2,47087 | -3,88396 | 6,105197 | |||
| -1,0126 | 4,050559 | -8,15215 | 16,40703 | -1,6643 | 21,75569 | -101,475 | 473,3102 | |||
| 0,0175 | 0,965306 | -0,94841 | 0,931816 | -0,6009 | 12,96648 | -46,691 | 168,1296 | |||
| 0,7265 | 0,074802 | -0,02046 | 0,005595 | -0,4452 | 11,8694 | -40,8925 | 140,8827 | |||
| 4,7046 | 13,72406 | 50,84216 | 188,3499 | -2,0503 | 25,50553 | -128,811 | 650,5321 | |||
| 0,9657 | 0,001176 | -4E-05 | 1,38E-06 | -0,2126 | 10,3208 | -33,1566 | 106,5189 | |||
| -0,5095 | 2,27859 | -3,43953 | 5,191974 | -0,364 | 11,3165 | -38,0687 | 128,0631 | |||
| 2,0503 | 1,10313 | 1,158618 | 1,216896 | 1,8807 | 1,252832 | -1,4023 | 1,569589 | |||
| 0,2493 | 0,56355 | -0,42306 | 0,317589 | 4,0108 | 1,021717 | 1,032751 | 1,043905 | |||
| -1,5933 | 6,725205 | -17,4405 | 45,22838 | -2,7746 | 33,34601 | -192,56 | 1111,956 | |||
| -0,6249 | 2,6403 | -4,29022 | 6,971184 | 0,2309 | 7,667915 | -21,2332 | 58,79692 | |||
| -1,1504 | 4,62422 | -9,94392 | 21,38341 | 2,9042 | 0,009178 | -0,00088 | 8,42E-05 | |||
| 0,0875 | 0,832656 | -0,7598 | 0,693316 | -1,8807 | 23,82123 | -116,264 | 567,4511 | |||
| 4,3315 | 11,09889 | 36,97596 | 123,1854 | -0,5543 | 12,63305 | -44,9016 | 159,5939 | |||
| -8,2416 | 85,40717 | -789,299 | 7294,385 | 7,1154 | 16,93652 | 69,70054 | 286,8456 | |||
| -0,3249 | 1,75536 | -2,32568 | 3,081289 | -1,8807 | 23,82123 | -116,264 | 567,4511 | |||
| -5,6713 | 44,50624 | -296,915 | 1980,806 | 0,2679 | 7,46437 | -20,3934 | 55,71683 | |||
| -0,581513 | 2,501183 | -3,95565 | 6,255918 | 0,1716017 | 7,999837 | -22,6267 | 63,99739 | |||
| -0,5872941 | 2,519503 | -3,99919 | 6,347894 | 0,1641818 | 8,041865 | -22,8053 | 64,67159 | |||
| -0,5930753 | 2,537889 | -4,04305 | 6,440881 | 0,156762 | 8,084002 | -22,9847 | 65,35109 | |||
| -0,5988565 | 2,556342 | -4,08722 | 6,534885 | 0,1493422 | 8,12625 | -23,1652 | 66,03594 | |||
| -0,6046377 | 2,574862 | -4,13172 | 6,629915 | 0,1419223 | 8,168608 | -23,3465 | 66,72616 | |||
| -0,6104189 | 2,593449 | -4,17654 | 6,725977 | 0,1345025 | 8,211076 | -23,5288 | 67,42177 | |||
| -0,6162 | 2,612103 | -4,22168 | 6,82308 | 0,1270826 | 8,253654 | -23,7121 | 68,12281 | |||
| -0,6219812 | 2,630823 | -4,26715 | 6,92123 | 0,1196628 | 8,296343 | -23,8963 | 68,8293 | |||
| -0,6277624 | 2,64961 | -4,31294 | 7,020436 | 0,1122429 | 8,339141 | -24,0814 | 69,54127 | |||
| -0,6335436 | 2,668465 | -4,35905 | 7,120704 | 0,1048231 | 8,382049 | -24,2675 | 70,25875 | |||
| -0,6393248 | 2,687386 | -4,4055 | 7,222042 | 0,0974032 | 8,425068 | -24,4546 | 70,98177 | |||
| -0,6451059 | 2,706374 | -4,45227 | 7,324458 | 0,0899834 | 8,468197 | -24,6426 | 71,71036 | |||
| -0,6508871 | 2,725428 | -4,49937 | 7,427959 | 0,0825635 | 8,511436 | -24,8316 | 72,44454 | |||
| -0,6566683 | 2,74455 | -4,54681 | 7,532554 | 0,0751437 | 8,554785 | -25,0215 | 73,18434 | |||
| -0,6624495 | 2,763738 | -4,59458 | 7,638249 | 0,0677238 | 8,598244 | -25,2124 | 73,92979 | |||
| -0,6682307 | 2,782994 | -4,64268 | 7,745053 | 0,060304 | 8,641813 | -25,4043 | 74,68093 | |||
| -0,6740118 | 2,802316 | -4,69111 | 7,852973 | 0,0528841 | 8,685492 | -25,5972 | 75,43777 | |||
| -0,679793 | 2,821705 | -4,73988 | 7,962017 | 0,0454643 | 8,729281 | -25,791 | 76,20035 | |||
| -0,6855742 | 2,84116 | -4,78899 | 8,072192 | 0,0380444 | 8,773181 | -25,9858 | 76,9687 | |||
| -0,6913554 | 2,860683 | -4,83843 | 8,183507 | 0,0306246 | 8,81719 | -26,1815 | 77,74284 | |||
| -0,6971366 | 2,880273 | -4,88822 | 8,29597 | 0,0232047 | 8,86131 | -26,3783 | 78,52281 | |||
| -0,7029177 | 2,899929 | -4,93834 | 8,409587 | 0,0157849 | 8,90554 | -26,576 | 79,30864 | |||
| -0,7086989 | 2,919652 | -4,98881 | 8,524368 | 0,0083651 | 8,94988 | -26,7748 | 80,10035 | |||
| -0,7144801 | 2,939442 | -5,03961 | 8,640319 | 0,0009452 | 8,99433 | -26,9745 | 80,89797 | |||
| -0,7202613 | 2,959299 | -5,09077 | 8,75745 | -0,0064746 | 9,03889 | -27,1752 | 81,70153 | |||
| -0,7260425 | 2,979223 | -5,14226 | 8,875767 | -0,0138945 | 9,08356 | -27,3769 | 82,51106 | |||
| -0,7318236 | 2,999213 | -5,19411 | 8,995279 | -0,0213143 | 9,12834 | -27,5796 | 83,3266 | |||
| -0,7376048 | 3,019271 | -5,2463 | 9,115994 | -0,0287342 | 9,173231 | -27,7833 | 84,14816 | |||
| -0,743386 | 3,039395 | -5,29884 | 9,23792 | -0,036154 | 9,218231 | -27,988 | 84,97579 | |||
| -0,7491672 | 3,059586 | -5,35173 | 9,361065 | -0,0435739 | 9,263342 | -28,1937 | 85,8095 | |||
| -0,7549484 | 3,079844 | -5,40497 | 9,485437 | -0,0509937 | 9,308563 | -28,4004 | 86,64934 | |||
| -0,7607295 | 3,100169 | -5,45856 | 9,611045 | -0,0584136 | 9,353894 | -28,6081 | 87,49533 | |||
| -0,7665107 | 3,12056 | -5,5125 | 9,737895 | -0,0658334 | 9,399335 | -28,8168 | 88,34749 | |||
| -0,7722919 | 3,141019 | -5,5668 | 9,865998 | -0,0732533 | 9,444886 | -29,0265 | 89,20587 | |||
| -0,7780731 | 3,161544 | -5,62146 | 9,99536 | -0,0806731 | 9,490547 | -29,2373 | 90,07048 | |||
| -0,7838543 | 3,182136 | -5,67647 | 10,12599 | -0,088093 | 9,536318 | -29,449 | 90,94136 | |||
| -0,7896354 | 3,202795 | -5,73184 | 10,2579 | -0,0955128 | 9,5822 | -29,6618 | 91,81855 | |||
| -0,7954166 | 3,223521 | -5,78756 | 10,39109 | -0,1029327 | 9,628191 | -29,8756 | 92,70206 | |||
| -0,8011978 | 3,244313 | -5,84365 | 10,52557 | -0,1103525 | 9,674293 | -30,0905 | 93,59194 | |||
| -0,806979 | 3,265173 | -5,9001 | 10,66135 | -0,1177724 | 9,720504 | -30,3063 | 94,48821 | |||
| -0,8127602 | 3,286099 | -5,95691 | 10,79845 | -0,1251922 | 9,766826 | -30,5232 | 95,3909 | |||
| -0,8185413 | 3,307093 | -6,01408 | 10,93686 | -0,1326121 | 9,813258 | -30,7411 | 96,30004 | |||
| -0,8243225 | 3,328153 | -6,07162 | 11,0766 | -0,1400319 | 9,8598 | -30,9601 | 97,21566 | |||
| -0,8301037 | 3,34928 | -6,12953 | 11,21767 | -0,1474517 | 9,906453 | -31,1801 | 98,1378 | |||
| -0,8358849 | 3,370473 | -6,1878 | 11,36009 | -0,1548716 | 9,953215 | -31,4011 | 99,06648 | |||
| -0,8416661 | 3,391734 | -6,24644 | 11,50386 | -0,1622914 | 10,00009 | -31,6232 | 100,0017 | |||
| -0,8474472 | 3,413061 | -6,30545 | 11,64899 | -0,1697113 | 10,04707 | -31,8463 | 100,9436 | |||
| -0,8532284 | 3,434456 | -6,36483 | 11,79548 | -0,1771311 | 10,09416 | -32,0705 | 101,8921 | |||
| -0,8590096 | 3,455917 | -6,42458 | 11,94336 | -0,184551 | 10,14136 | -32,2957 | 102,8473 | |||
| -0,8647908 | 3,477445 | -6,48471 | 12,09262 | -0,1919708 | 10,18868 | -32,522 | 103,8092 | |||
| -0,8705719 | 3,499039 | -6,5452 | 12,24328 | -0,1993907 | 10,2361 | -32,7493 | 104,7778 | |||
| -0,8763531 | 3,520701 | -6,60608 | 12,39534 | -0,2068105 | 10,28363 | -32,9777 | 105,7531 | |||
| -0,8821343 | 3,54243 | -6,66733 | 12,54881 | -0,2142304 | 10,33128 | -33,2071 | 106,7353 | |||
| -0,8879155 | 3,564225 | -6,72896 | 12,7037 | -0,2216502 | 10,37903 | -33,4376 | 107,7243 | |||
| -0,8936967 | 3,586087 | -6,79096 | 12,86002 | -0,2290701 | 10,42689 | -33,6692 | 108,7201 | |||
| -0,8994778 | 3,608016 | -6,85335 | 13,01778 | -0,2364899 | 10,47487 | -33,9018 | 109,7228 | |||
| -0,905259 | 3,630012 | -6,91611 | 13,17699 | -0,2439098 | 10,52295 | -34,1355 | 110,7325 | |||
| -0,9110402 | 3,652075 | -6,97926 | 13,33765 | -0,2513296 | 10,57114 | -34,3703 | 111,7491 | |||
| -0,9168214 | 3,674204 | -7,04279 | 13,49978 | -0,2587495 | 10,61945 | -34,6061 | 112,7727 | |||
| -0,9226026 | 3,696401 | -7,10671 | 13,66338 | -0,2661693 | 10,66786 | -34,843 | 113,8033 | |||
| -0,9283837 | 3,718664 | -7,17101 | 13,82846 | -0,2735892 | 10,71639 | -35,081 | 114,8409 | |||
| -0,9341649 | 3,740994 | -7,2357 | 13,99504 | -0,281009 | 10,76502 | -35,3201 | 115,8857 | |||
| -0,9399461 | 3,763391 | -7,30078 | 14,16311 | -0,2884289 | 10,81376 | -35,5603 | 116,9375 | |||
| -0,9457273 | 3,785855 | -7,36624 | 14,3327 | -0,2958487 | 10,86262 | -35,8015 | 117,9965 | |||
| -0,9515085 | 3,808385 | -7,4321 | 14,5038 | -0,3032685 | 10,91158 | -36,0439 | 119,0626 | |||
| -0,9572896 | 3,830983 | -7,49834 | 14,67643 | -0,3106884 | 10,96066 | -36,2873 | 120,136 | |||
| -0,9630708 | 3,853647 | -7,56498 | 14,8506 | -0,3181082 | 11,00984 | -36,5318 | 121,2166 | |||
| -0,968852 | 3,876378 | -7,63201 | 15,02631 | -0,3255281 | 11,05914 | -36,7775 | 122,3045 | |||
| -0,9746332 | 3,899176 | -7,69944 | 15,20358 | -0,3329479 | 11,10854 | -37,0242 | 123,3997 | |||
| -0,9804144 | 3,922041 | -7,76727 | 15,38241 | -0,3403678 | 11,15806 | -37,272 | 124,5022 | |||
| -0,9861955 | 3,944973 | -7,83549 | 15,56281 | -0,3477876 | 11,20768 | -37,5209 | 125,6121 | |||
| -0,9919767 | 3,967971 | -7,90411 | 15,7448 | -0,3552075 | 11,25742 | -37,771 | 126,7294 | |||
| -0,9977579 | 3,991037 | -7,97312 | 15,92837 | -0,3626273 | 11,30726 | -38,0221 | 127,8542 | |||
| -1,0035391 | 4,014169 | -8,04254 | 16,11355 | -0,3700472 | 11,35722 | -38,2744 | 128,9864 | |||
| -1,0093203 | 4,037368 | -8,11237 | 16,30034 | -0,377467 | 11,40728 | -38,5277 | 130,1261 | |||
| -1,0151014 | 4,060634 | -8,18259 | 16,48875 | -0,3848869 | 11,45746 | -38,7822 | 131,2734 | |||
| -1,0208826 | 4,083967 | -8,25322 | 16,67878 | -0,3923067 | 11,50774 | -39,0378 | 132,4282 | |||
| -1,0266638 | 4,107366 | -8,32425 | 16,87046 | -0,3997266 | 11,55814 | -39,2945 | 133,5906 | |||
| -1,032445 | 4,130833 | -8,39569 | 17,06378 | -0,4071464 | 11,60865 | -39,5524 | 134,7607 | |||
| -1,0382262 | 4,154366 | -8,46754 | 17,25876 | -0,4145663 | 11,65926 | -39,8113 | 135,9384 | |||
| -1,0440073 | 4,177966 | -8,53979 | 17,4554 | -0,4219861 | 11,70999 | -40,0714 | 137,1238 | |||
| -1,0497885 | 4,201633 | -8,61246 | 17,65372 | -0,429406 | 11,76083 | -40,3326 | 138,317 | |||
| -1,0555697 | 4,225367 | -8,68554 | 17,85372 | -0,4368258 | 11,81177 | -40,595 | 139,5179 | |||
| -1,0613509 | 4,249167 | -8,75903 | 18,05542 | -0,4442457 | 11,86283 | -40,8585 | 140,7267 | |||
| -1,0671321 | 4,273035 | -8,83293 | 18,25883 | -0,4516655 | 11,91399 | -41,1231 | 141,9433 | |||
| -1,0729132 | 4,296969 | -8,90724 | 18,46395 | -0,4590853 | 11,96527 | -41,3889 | 143,1677 | |||
| -1,0786944 | 4,32097 | -8,98198 | 18,67079 | -0,4665052 | 12,01666 | -41,6558 | 144,4001 | |||
| -1,0844756 | 4,345039 | -9,05713 | 18,87936 | -0,473925 | 12,06816 | -41,9239 | 145,6404 | |||
| -1,0902568 | 4,369173 | -9,13269 | 19,08968 | -0,4813449 | 12,11976 | -42,1931 | 146,8886 | |||
| -1,096038 | 4,393375 | -9,20868 | 19,30174 | -0,4887647 | 12,17148 | -42,4634 | 148,1449 | |||
| -1,1018191 | 4,417644 | -9,28509 | 19,51558 | -0,4961846 | 12,22331 | -42,7349 | 149,4092 | |||
| -1,1076003 | 4,441979 | -9,36192 | 19,73118 | -0,5036044 | 12,27524 | -43,0076 | 150,6816 | |||
| -1,1133815 | 4,466381 | -9,43917 | 19,94856 | -0,5110243 | 12,32729 | -43,2814 | 151,9621 | |||
| -1,1191627 | 4,49085 | -9,51684 | 20,16774 | -0,5184441 | 12,37945 | -43,5564 | 153,2508 | |||
| -1,1249439 | 4,515386 | -9,59494 | 20,38871 | -0,525864 | 12,43172 | -43,8325 | 154,5476 | |||
| -1,130725 | 4,539989 | -9,67347 | 20,6115 | -0,5332838 | 12,48409 | -44,1098 | 155,8526 | |||
| -1,1365062 | 4,564659 | -9,75242 | 20,83611 | -0,5407037 | 12,53658 | -44,3883 | 157,1659 | |||
| -1,1422874 | 4,589395 | -9,8318 | 21,06255 | -0,5481235 | 12,58918 | -44,668 | 158,4875 | |||
| -1,1480686 | 4,614199 | -9,91161 | 21,29083 | -0,5555434 | 12,64189 | -44,9488 | 159,8173 | |||
| -1,1538497 | 4,639069 | -9,99186 | 21,52096 | -0,5629632 | 12,69471 | -45,2308 | 161,1556 | |||
| -1,1596309 | 4,664006 | -10,0725 | 21,75295 | -0,5703831 | 12,74764 | -45,5139 | 162,5022 | |||
| -1,1654121 | 4,68901 | -10,1536 | 21,98681 | -0,5778029 | 12,80067 | -45,7983 | 163,8572 | |||
| -1,1711933 | 4,71408 | -10,2352 | 22,22255 | -0,5852228 | 12,85382 | -46,0838 | 165,2207 | |||
| -1,1769745 | 4,739218 | -10,3172 | 22,46019 | -0,5926426 | 12,90708 | -46,3705 | 166,5927 | |||
| -1,1827556 | 4,764422 | -10,3996 | 22,69972 | -0,6000625 | 12,96045 | -46,6584 | 167,9733 | |||
| -1,1885368 | 4,789693 | -10,4824 | 22,94116 | -0,6074823 | 13,01393 | -46,9475 | 169,3623 | |||
| -1,194318 | 4,815032 | -10,5657 | 23,18453 | -0,6149021 | 13,06752 | -47,2378 | 170,76 | |||
| -1,2000992 | 4,840436 | -10,6494 | 23,42982 | -0,622322 | 13,12122 | -47,5293 | 172,1663 | |||
| -1,2058804 | 4,865908 | -10,7336 | 23,67706 | -0,6297418 | 13,17503 | -47,8219 | 173,5813 | |||
| -1,2116615 | 4,891447 | -10,8182 | 23,92625 | -0,6371617 | 13,22895 | -48,1158 | 175,005 | |||
| -1,2174427 | 4,917052 | -10,9033 | 24,1774 | -0,6445815 | 13,28297 | -48,4109 | 176,4374 | |||
| -1,2232239 | 4,942725 | -10,9888 | 24,43053 | -0,6520014 | 13,33711 | -48,7072 | 177,8786 | |||
| -1,2290051 | 4,968464 | -11,0747 | 24,68563 | -0,6594212 | 13,39136 | -49,0046 | 179,3286 | |||
| -1,2347863 | 4,99427 | -11,1611 | 24,94273 | -0,6668411 | 13,44572 | -49,3033 | 180,7875 | |||
| -1,2405674 | 5,020142 | -11,248 | 25,20183 | -0,6742609 | 13,50019 | -49,6032 | 182,2552 | |||
| -1,2463486 | 5,046082 | -11,3353 | 25,46294 | -0,6816808 | 13,55477 | -49,9043 | 183,7319 | |||
| -1,2521298 | 5,072089 | -11,423 | 25,72608 | -0,6891006 | 13,60946 | -50,2067 | 185,2175 | |||
| -1,257911 | 5,098162 | -11,5112 | 25,99126 | -0,6965205 | 13,66426 | -50,5102 | 186,7121 | |||
| -1,2636922 | 5,124302 | -11,5998 | 26,25847 | -0,7039403 | 13,71917 | -50,815 | 188,2157 | |||
| -1,2694733 | 5,150509 | -11,6889 | 26,52775 | -0,7113602 | 13,77419 | -51,121 | 189,7284 | |||
| -1,2752545 | 5,176783 | -11,7785 | 26,79908 | -0,71878 | 13,82932 | -51,4282 | 191,2
Поиск по сайту©2015-2024 poisk-ru.ru
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование. Дата создания страницы: 2019-11-10 Нарушение авторских прав и Нарушение персональных данных |
Поиск по сайту: Читайте также: Деталирование сборочного чертежа Когда производственнику особенно важно наличие гибких производственных мощностей? Собственные движения и пространственные скорости звезд |