Для любой дискретной СВ X – числовая функция F(x) = Р(Х < х),
-∞ < х < +∞ называется функцией распределения (ФР) этой СВ, а функция f(х) = F'(x), называется плотностью распределения или плотностью вероятности (ПВ) этой СВ.
Приведем графики возможных ФР F(x)и ПВ f(х)при равномерном законе распределения.

Рисунок 4 – Функция распределения при равномерном законе
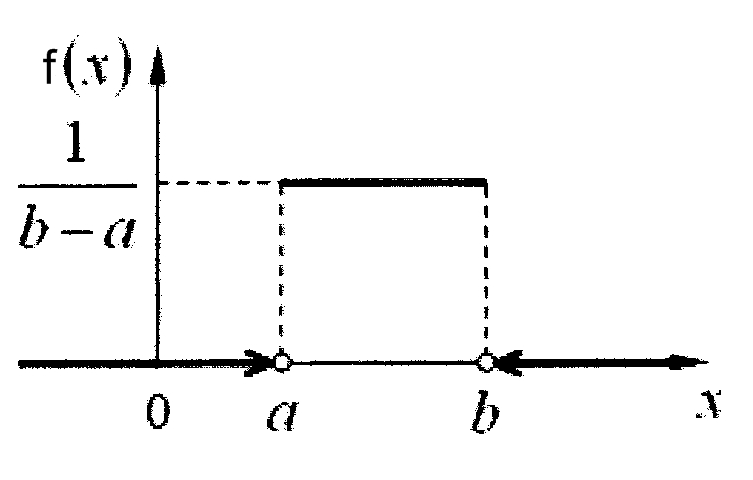
Рисунок 5 – Плотность вероятности при равномерном законе
ФР любой случайной величины обладает следующими свойствами:
- F(x) определена на всей числовой прямой R;
- F(x) не убывает, т.е. если x1 ≤ x2, то F(x1) ≤ F(x2);
- F(-∞)=0, F(+∞)=1, т.е.  и
и 
- F(x) непрерывна справа, т.е.. 
ПВ любой случайной величины обладает следующими свойствами:
- плотность распределения – неотрицательная функция f(x) ≥ 0;
- несобственный интеграл от плотности распределения в пределах от - ∞ до +∞ равен единице:

Рассмотрим основные числовые характеристики СП.
Математическое ожидание – мера среднего значения случайной величины, определяется формулой:

Дисперсия случайной величины – мера разброса данной случайной величины, то есть её отклонения от математического ожидания:

Абсолютны центральны момент k-го порядка СВ X:
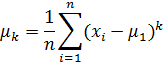
Коэффициент ассиметрии – числовая характеризующая степени несимметричности распределения СВ:

Коэффициент эксцесса – числовая характеризующая степени остроты пика распределения СВ:

Для коэффициента ассиметрии и эксцесса Ẋ – среднее значение:

Описание аналогов системы
На кафедре ИСТ СГАУ под руководством Прохорова С. А. была разработана автоматизированная информационная система для моделирования и аппроксимативного корреляционно-спектрального анализа СП [1]. В системе реализованы следующие функции:
- генерация СП с заданным видом КФ;
- проверка результатов моделирования;
- расчет числовых и вероятностных характеристик СП;
- визуализация полученных результатов.
Вид формы генерирования СП с заданным видом КФ и интерфейс экранной формы генерирования и оценки статистических характеристик случайного процесса представлены на рисунках 7 – 8.

Рисунок 7 – Вид формы генерирования СП с заданным видом КФ

Рисунок 8 – Интерфейс экранной формы генерирования и оценки статистических характеристик случайного процесса
На кафедре информационных технологий и систем автоматизированного проектирования Государственного образовательного учреждения, высшего профессионального образования «Московского государственного текстильного университета имени А.Н. Косыгина» Подрезовой В.И. был разработан автоматизированный программный комплекс «Компьютерное моделирование процессов деления потоков волокнистого материала и управления ими». В комплексе реализованы следующие функции:
- задание параметров моделирования;
- проведение экспериментов;
- просмотр результатов моделирования [3].

Рисунок 9 – Графическое представление работы комплекса